大阪府B問題｜公立高校入試確率問題2024

　２から６までの自然数が書いてある５枚のカード［２］、［３］、［４］、［５］、［６］が箱に入っている。この箱から２枚のカードを同時に取り出し、取り出した２枚のカードに書いてある数の和を$${a}$$、積を$${b}$$とするとき、$${b-a}$$の値が偶数である確率はいくらですか。どのカードが取り出されることも同様に確からしいものとして答えなさい。

分類：１５　同時に２つ取り出す

表をかいて考えます。

　まずは，すべての場合をどのように数え上げるか，ということを考えます。２枚のカードを同時に取り出しますので，たとえば［３］を２枚，というのは取り出せません。また，２枚取り出すときに「同時に」といいながら微妙に時間差がついたときに，［２］→［５］と取り出しているときと，［５］→［２］と取り出しているときとが考えられますが，これは順序関係なく１つの取り出し方と考えていいわけです。
　ですから，すべての場合を表をかいて表すと，対角線と左下を消して，次のようになります。

　起こりうるすべての場合は１０通り，と考えるわけです。
　この各マスに，$${a}$$とか$${b}$$とか$${b-a}$$とかの値を入れていきます。判断する条件は$${b-a}$$なので，かいて並べるときは$${b}$$→
$${a}$$の順番にしておくと，次に進むときに誤解がなくていいかもしれません。

　$${b-a}$$が偶数になるのは✓をつけた３通りですので，確率を求めると$${\dfrac{3}{10}}$$

答

$${\bm{\dfrac{3}{10}}}$$

もうちょっとスピードアップするために

　偶数・奇数の問題なので，２つのカードが｛偶数，偶数｝｛奇数，奇数｝｛偶数，奇数｝の組合せで，それぞれ$${b-a}$$の値がどうなるかで条件を絞ってみる，というアプローチをしてみてもいいでしょう。それぞれの場合について

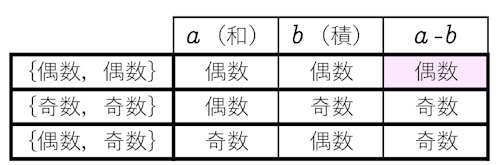
ですから，条件に合うのは２枚とも偶数であるときのみ。
　したがって｛２，４｝，｛２，６｝，｛４，６｝の３通りということになります。