
石川県|公立高校入試確率問題2023
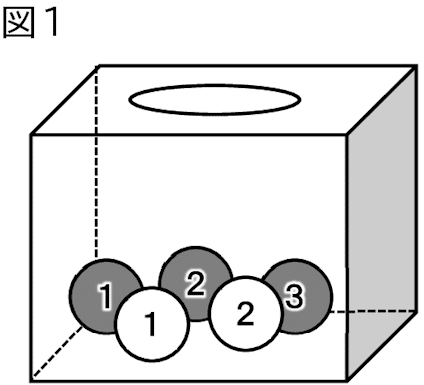
図1のように箱の中に,箱の中に1,2,3の数字が1つずつ書かれた3個の赤玉と,1,2の数字が1つずつ書かれた2個の白玉が入っている。
このとき,次の(1),(2)に答えなさい。
(1) 箱から玉を2個同時に取り出すとき,玉に書かれた数の和が4になる玉の取り出し方は,全部で何通りあるか,求めなさい。
(2) 図2のように,座標軸と原点Oがある。
箱から玉を1個ずつをもとにもどさずに続けて2回取り出す。1回目に取り出した玉の色と数字によって,点Pを□の中の規則にしたがって座標軸上にとる。
また,2回目に取り出した玉の色と数字によって,点Qを□の中の規則にしたがって座標軸上にとる。
〈 規則 〉
・赤玉を取り出したときは,玉に書かれた数を$${x}$$座標として$${x}$$軸上に点をとる。
・白玉を取り出したときはを玉に書かれた数を$${y}$$座標として$${y}$$軸上に点をとる。
このとき,O,P,Qを線分で結んだ図形が三角形になる確率を求めなさい。また,その考え方を説明しなさい。説明においては,図や表,式などを用いてよい。ただし,どの玉が取り出されることも同様に確からしいとする。

分類:《D3》座標平面上の図形-角度
同時に2つ取り出すそのことが
「同時に2つ取り出す」なので,表を考えます。
対角線を消して,左下を消したC型の表をかいて考えるのがよいですね。
赤玉をただの[1] 白玉を[①]のようにかいて区別します。(もちろん赤1,白1とか,R1,W1のようにかいてもいいです。)

当てはまる「2つの玉に書かれた数の和が4になる」場合は,表のように3通りあります。
(2)三角形ができる条件とは?
3つの点が一直線に並ぶと,三角形にはなりません。そのことが2回とも同じ色だと,どちらかの座標軸上に3つの点が並ぶことになります。それ以外,つまり1回目と2回目が異なる色を取り出すなら,O,P,Qを線分で結んだ図形は三角形になります。
つまり結局は「1回目に取り出した玉の色」と「2回目に取り出した玉の色」が異なる確率は? ということになります。
まず,この「言い換え」に気づけるかどうか。
そこさえ押さえれば,あとは表(や図)をかいて数えるだけ。もとに戻さずに続けて2回取り出しますので(1)と違って,順序がありますので,対角線だけを消して,左下を消さない(P型の)表をかいて,すべての場合を考えることになります。

当てはまる場合は12通りで,起こりうるすべての場合は20通りありますので,求める確率は$${\dfrac{12}{20}=\bm{\dfrac{3}{5}}}$$
答
(1)3通り
(2)$${\bm{\dfrac{3}{5}}}$$
O,P,Qを線分で結んだ図形が三角形になるのは,「1回目に取り出した玉の色」と「2回目に取り出した玉の色」が異なるときなので,その確率を求めればよい。
赤球を1・2・3,白球を①・②と表して表をかくと,上の表のとおりで,起こりうるすべての場合の数は20通りで,玉の色が異なる場合は12通りであるから,その確率は$${\dfrac{12}{20}=\dfrac{3}{5}}$$と求められる。
【研究】確率の積の法則で解けるのだが・・・
(2)について,中学標準レベルなら以上でおしまいでよいでしょう。これを確率の積の法則を使いこなせる上位層の子たちが解いたら・・・? というか,高校の試験や大学入試で求められる答案ということで考えてみます。
1回目と2回目で異なる色の玉を取り出せばすのですから,(1)1回目で赤玉をひく場合と,(2)1回目で白玉をひく場合に分けて考えます。
(1)1回目に赤玉・2回目に白玉をひく場合
1回目に5個の玉の中から3個の赤玉のうちの1つ,2回目に残り4個の玉の中から2個の白玉のうちの1つをひけばよいのですから,その確率は
$${\dfrac{3}{5}×\dfrac{2}{4}=\dfrac{3}{10}}$$
(2)1回目に白玉・2回目に赤玉をひく場合
1回目に5個の玉の中から2個の白玉のうちの1つ,2回目に残り4個の玉の中から3個の赤玉のうちの1つをひけばよいのですから,その確率は
$${\dfrac{2}{5}×\dfrac{3}{4}=\dfrac{3}{10}}$$
(1)と(2)は同時には起こらないので,(1)か(2)のどちらかが起こる確率は,
$${\dfrac{3}{10}+\dfrac{3}{10}=\dfrac{3}{5}}$$
と求めるのが高校生っぽい(高校の試験や大学入試における)解き方になります。
う~ん,考え方を書きなさいとなっているので,積の法則を使いこなしている上位層は,たぶんこういう解答を高校入試の答案に書くことになるのではと思うのですが,果たしてこれで逆に○をもらったのかどうかは気になるところ。
ちなみに解答例は樹形図をかいてます。
この記事が気に入ったらサポートをしてみませんか?
