確率ウェイト関数 確率加重関数 (行動経済学用語集 プロスペクト理論 関連)
【非線形な確率荷重関数とアレのパラドックス(背理ともいう、ここでは確実性効果Certainty effect)の説明】
参考:心理物理学的に、確率ウェイト関数(確率加重関数)の関数形を導出した研究論文はこちらのリンク (PDFはこちら) 日本語解説はこちら
プロスペクト理論においては、リスクを伴う報酬や損失などの結果(outcome)の価値はv(Δx)w(p) (Δx:厚生変化、p:その厚生変化が生じる確率)と価値観数vと確率ウェイト関数wとの積に分解できると仮定されている。確率ウェイト関数(probability weighting function)は、確率荷重関数とも訳されることがある。初心者むけの動画による説明も参照のこと。
w(p)は、Prelec (Econometrica, 1998)によって、以下の関数形であることが求められた:
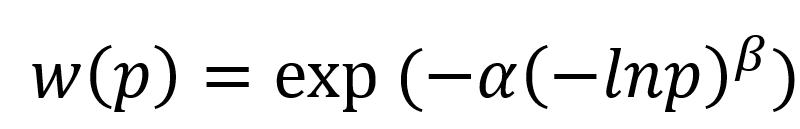
0<α、β≦1、pは厚生変化が生じる確率。
現在では、この関数は、以下の公理(power invariance)から導出されることが知られている(al-Nowaihi, A., Dhami, S., 2006. Journal of Mathematical Psychology 50 (6), 521-524.)。
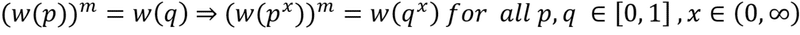
w(1)=1, w(0)→0 であることは容易に分かる。α=1、β=0.6の場合を以下に示す。http://fooplot.com/ による。2020年12月10日訪問
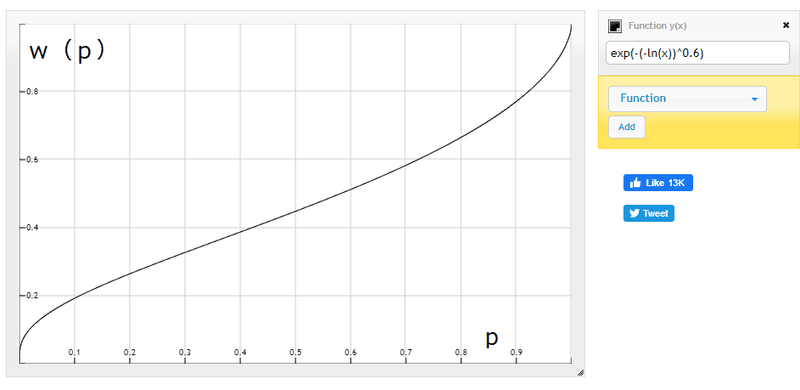
確率判断やリスク下の意思決定における「アノマリー」がどのような場合に生じて、また、どのような場合には生じないか、を分析するために、まずこの関数の確率による一階微分を求めておく必要がある:
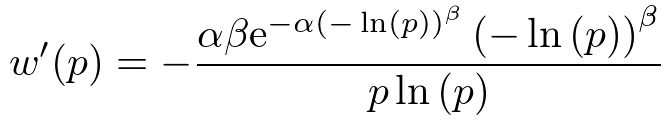
プロスペクト理論の理解度チェック
Q1 この関数から、確実性効果(Certainty effect, Allais, 1953)の存在証明をせよ(存在可能条件を特定し、その条件ではこの効果が発生するということを論証せよ)。さらに、この確実性効果が存在する必要十分条件を演繹的に導出せよ。
(ヒント: 以下の極限が無限大に発散することが確実性効果である)
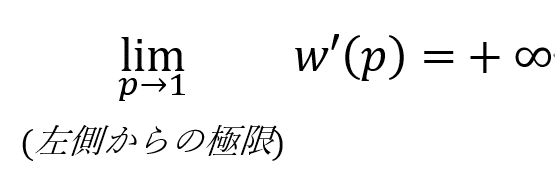
Q2 α=1と単純化した場合に、確率判断エラーがおこらない場合
(すなわち、βによらず、生じうる厚生変化の符号が各結果ごとに異ならなければ期待効用アノマリーが生じない場合)
が、p=1/e(およそ37パーセントの確率・頻度)でおこる事象についての判断を行う場合であるということを論証せよ。
Q3 非常に小さな確率や頻度で発生する事象が、実際以上に過大に評価される場合がある、という存在証明を、この関数を用いて論証(演繹)せよ。
(ヒント: このことは、w(0)=∞を意味しない。
たとえば、α=1、β=0.8として
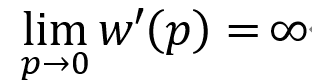
を示せばよい)
さらに、この効果が存在する必要十分条件の特定をせよ。
Q4 (★やや発展的)上記のQ2で「生じうる厚生変化の符号が各結果ごとに異ならなければ」という但し書きが必要であるのは、人間に損失回避性があるからなのか、人間が結果(outcome)ではなく変化に反応するからなのか、またはそれら両方だからなのか、それとも全く異なる理由からなのか、価値関数と確率ウェイト関数双方の数学的性質から理由を特定せよ。
(参考:w(p)とその一回微分を、α=1、β=0.8の場合にプロットしたグラフ をみると、p=0でw(p)の微係数がプラス無限大に発散=ごくわずかな発生確率の過大評価、p=1で左側からの微係数がプラス無限大に発散=確実性効果が起こっていることがわかる)
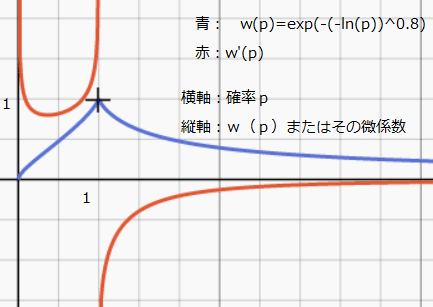
https://www.derivative-calculator.net/ (2020年8月18日訪問)
における数式・数値処理を利用
-------------------------以下に略解を示す-----------------------------------------
Q1の略解
答えは、0<α、かつ 0<β<1 ⇔ Allaisの「確実性効果」が存在する
である。確実性効果の存在条件(必要十分条件)においては、αには上限の制限がないが、βには下限と上限が制約条件となる。その(簡略的な)論証を以下に示す。
(まず、α=1と固定した場合の説明のみ記す)
0<β<1となる場合は、(βをコサインの2乗で置き換えて,ただしθ≠±nπとしてcosθ≠1かつsinθ≠0となるようにしてβ≠0となるように見やすくするという)以下の式変形ができるので「確実性効果」がおきる。そうでない場合は、確実性効果はおこらない。
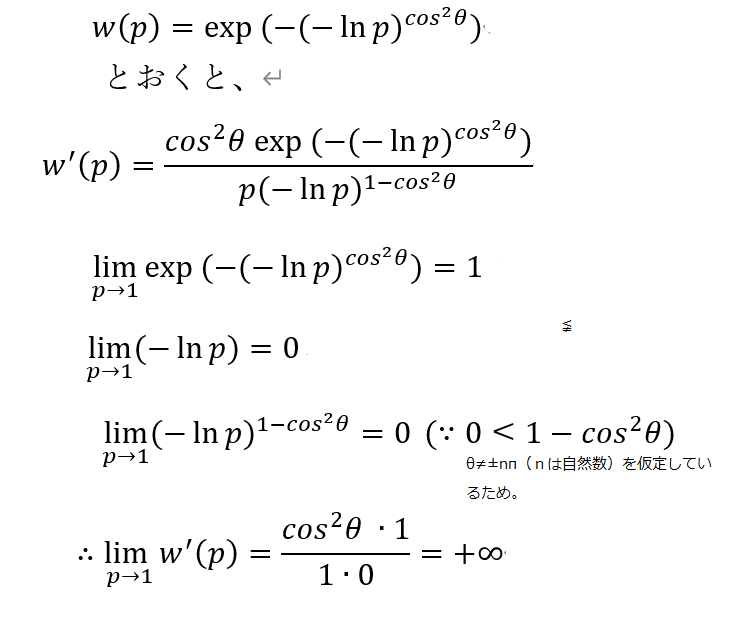
次に、αもフリーパラメータとして動かした場合はどうなるか、考えてみると、
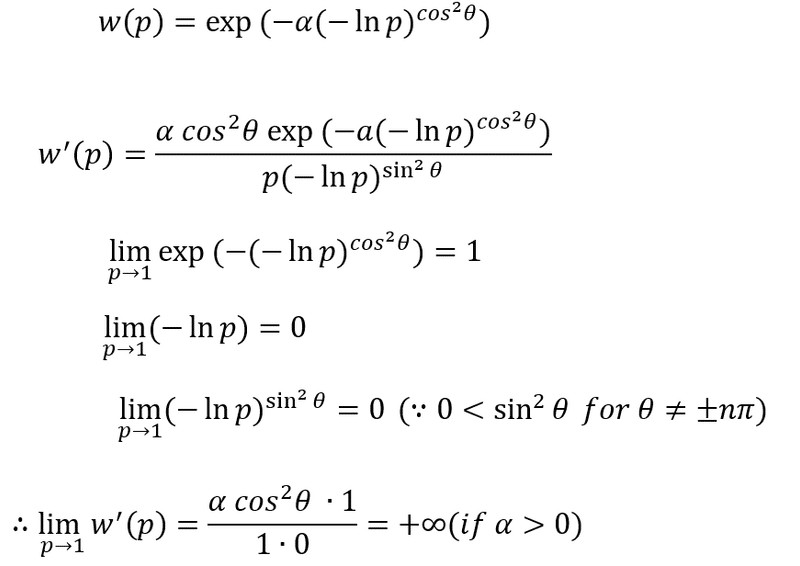
となることから、先の主張の妥当性のうち、十分性(「⇒」のこと)が論証された。
実際にα=10>1、β=0.65<1の場合に上記のように、赤いカーブでw'(p)(一回微分)を描くと、p=1で+無限大に発散していること、αは1より大きいけれどもβが1未満であるおかげで「確実性効果」が発生していること、が見て取れる。
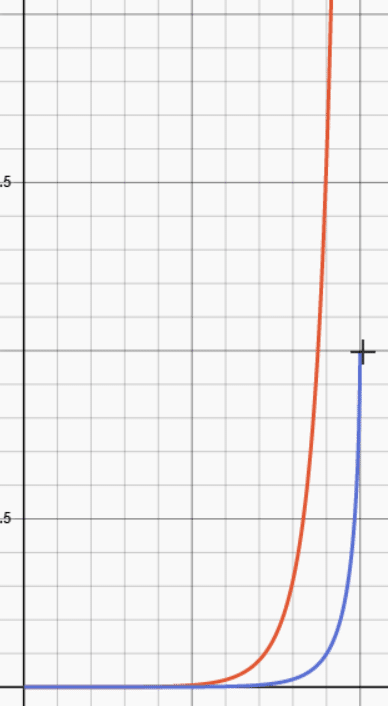
https://www.derivative-calculator.net/ (2020年8月18日訪問 グラフ描画に用いた)
Q2は直接w(1/e)=1/eが示せるので自明
Q3:答え(必要十分条件)0<α、かつ 0<β<1
以下の関係を利用すると、α>0 ならば w'(p=0)=+∞ が示せる。(α<0ならば、「小さい確率の過大評価」が起こらないことがわかる)
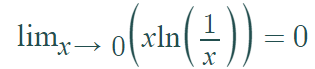
(関連するnote記事:条件付確率判断)
この記事が気に入ったらサポートをしてみませんか?
