
GeoGebraとベクトルで遊ぶ
ハロウィンが間近に迫っている今日この頃。ミケはGeoGebraで遊んでいました。どうやらベクトルを書いているようです。
ミケ:この前はベクトル場を描画して遊んでいたけど、今回は純粋にベクトルを書くぞ!
ミケ:このGeoGebraは無料なのにめちゃくちゃ便利!ありがたいなぁ。
ミケ:まずこのベクトルの角度を表示させたいな。よーし、調べてみよう!
使うサイトについて
今回使うサイトは、GeoGebraの「幾何」だよ!
前回の「関数グラフ」と違ってより幾何学的なことをしたい時に適しているよ。
間違って「関数グラフ」のほうを使うとうまくいかないこともあるからその点注意してね。
下準備
さっき紹介した「幾何」のサイトを開くと次のようになってると思う。

もちろんこのまま使ってもいいんだけど、最初は分かりやすくするために軸を出してあげよう。
まず右上にある歯車マークをクリックしてみて。

そうしたら下の写真みたいにいろいろ選択できる項目が出るから、赤で囲っている一番上の[軸を表示]を押してみて!

すると軸が表示されるから、そのあと上から二番目の[グリッドを表示]をクリックしてみて!

そうするとさらにいろいろ項目が現れるから、そのなかで紫で囲ったところをクリックしてみて!

こんな感じで極座標が現れたら成功だよ!

それじゃあ試しにベクトルを表示させてみよう。
左側の入力欄に
Vector((1,1))と入力してみよう。
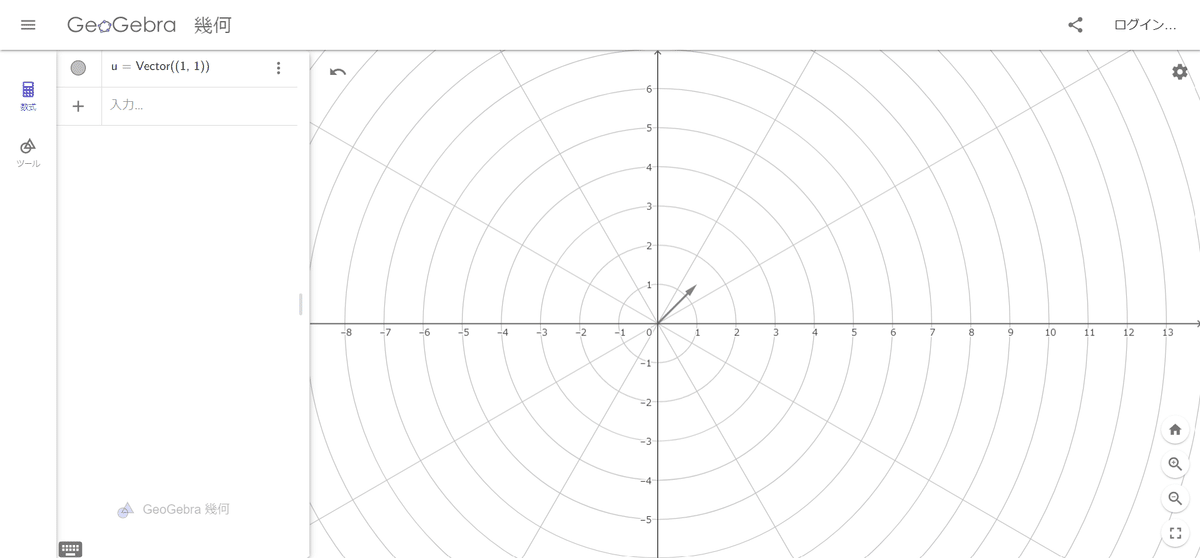
こんな感じでベクトルが表示されるね。
じゃあ次に大きさと角度を指定してベクトルを表示させてみよう。
左側の入力欄に
Vector(( 1.414 ;45°))と入力してみて!
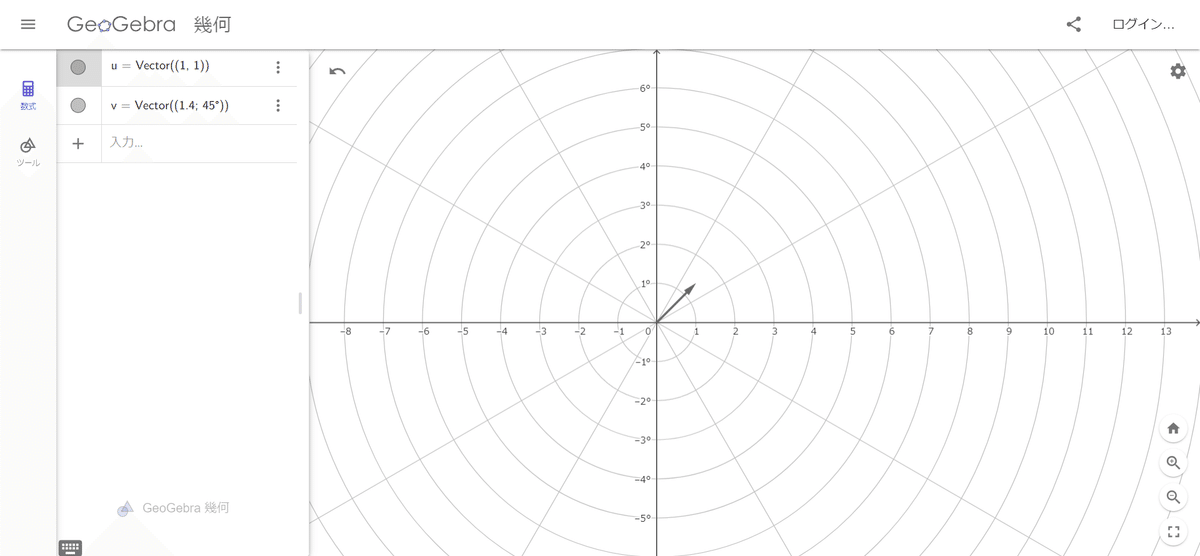
なんかぱっとみ何か変わったようには見えないね…。でもそれは当たり前なんだよね。
だって$${\vec{a}=[1,1]=\sqrt{2}\angle45\degree\approx1.414\angle45\degree}$$だから、さっき入力したベクトルは(ほぼ)同じものだからだね。
とはいえこのまま重なっていたら具合が悪いから、角度と大きさで入力したほうに色を付けてみよう。
入力欄の上から二番目(写真の場合だとv=…のところ)の欄の三点リーダをクリックしてみて!
すると[設定]という選択が見つかるはずだからそれをクリック!

そうすると上の写真みたいに右側に設定画面が出てくるよね。今度はそのなかの赤で囲った[色]タブをクリックしてみて!

クリックしたら色を選択する画面が出てくるから、今回は緑で囲っている[赤]を選択してみよう!

こんな感じで赤色が出てきたら成功だよ!
それじゃあ最後にベクトルをマウスで伸ばしてみよう。でもこれはとっても簡単で、対象のベクトルをマウスでクリックしたまま動かすだけ!
試しに赤のベクトルの矢印の先端をクリックしてそのまま横に伸ばしてみよう!
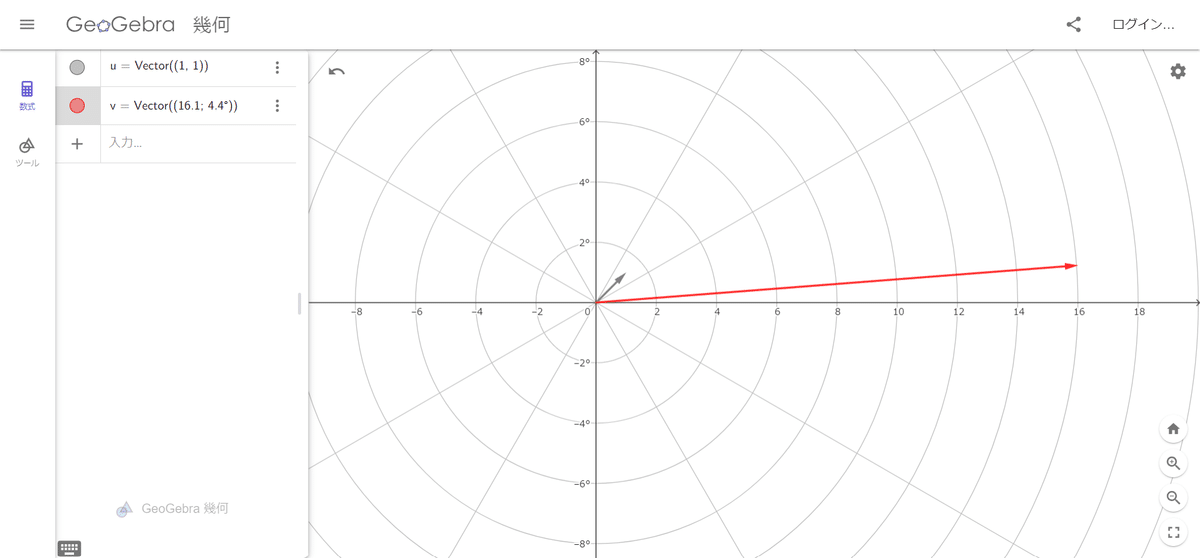
ちゃんと入力欄の数値も変わっているね!
ベクトルの角度を表示する
じゃあベクトルの角度を表示していこう!
入力欄に
Angle(v)と入力してみよう!

こんな感じで角度が表示されれば成功だよ!このとき数値が4.4°じゃなくても大丈夫だからね!
試しにこの赤いベクトルを動かしてみて角度が変化するかを見てみよう。
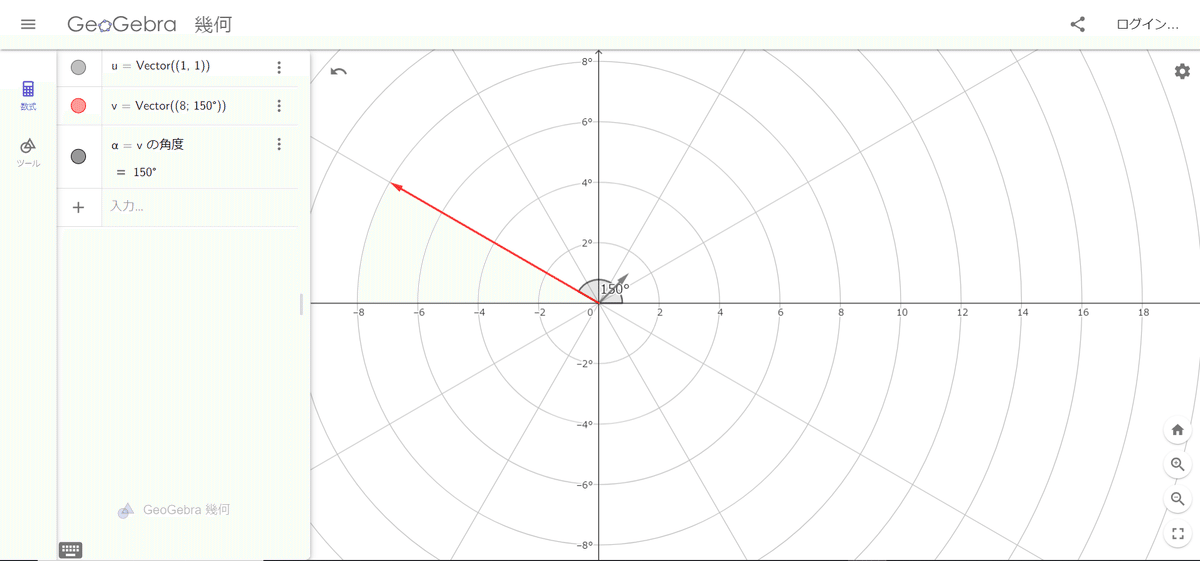
第二象限のところに適当に動かしてみると、ちゃんと角度も変わっていることがわかるね。
じゃあ次に内積の計算で求めた角度がほんとに二つのベクトルのなす角度なのかを確かめていこう。
試しに$${\vec{a}=[5,10],\vec{b}=[6,2]}$$の二つのベクトルで考えていこう。
内積を計算して求めると、
$${\vec{a}\cdot\vec{b}=[5,10]\cdot[6,2]=50=\|\vec{a}\|\|\vec{b}\|\cos\theta=\sqrt{5^2+10^2}\cdot\sqrt{6^2+2^2}\cos\theta=50\sqrt{2}\cos\theta}$$
よって変形して
$${\cos\theta=\frac{1}{\sqrt{2}}\rightarrow \theta=45\degree}$$
となるね。
じゃあ次に二つのベクトルをGeoGebraに入力してみると

確かに45°っぽいね。数値だけ見ても全然45°じゃなさそうだけど図で見ると理解が進むよね。
等速円運動をベクトルでみる
それじゃあ今度は等速円運動とベクトルを絡めて遊んでいこう。
とりあえず等速円運動の軌跡をを作ろう。円運動だから単純に円の方程式を使えばいいね。半径はとりあえず1にしておくよ。
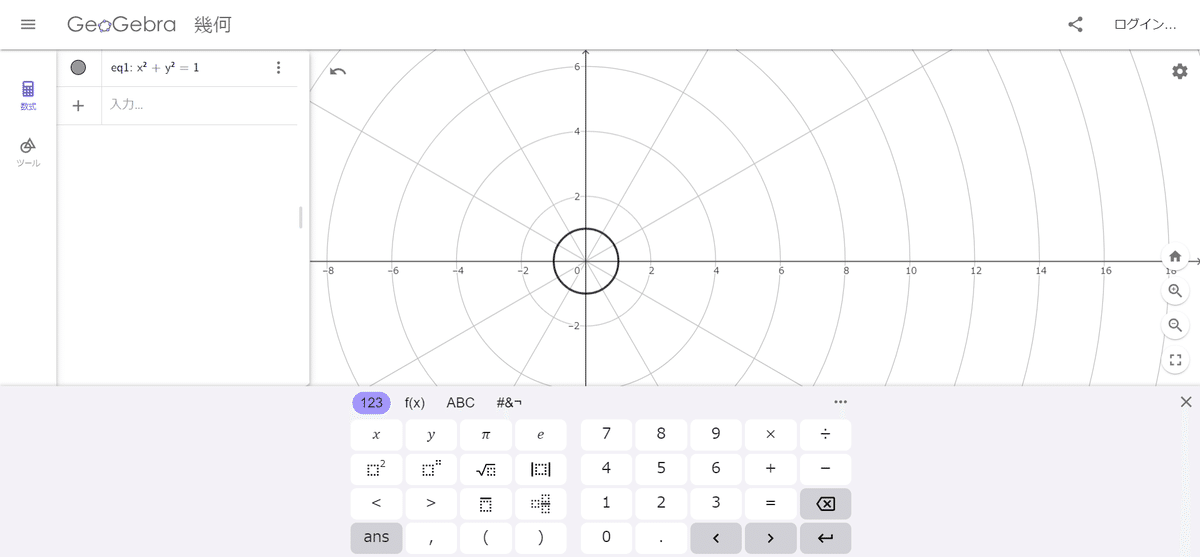
次に運動する際に必要なパラメータtを用意しておくよ。
入力欄にt=πと入力して、三点リーダから[設定]をクリックしよう!

そのあと上図のように[スライダー]をクリックしてみて。
ここでパラメータの変動に関する設定ができるよ。試しにtの変域を
$${0\leq t\leq 2\pi}$$にしてみよう。
[最小]の入力欄に0、[最大]の入力欄に2πを入力してみて!
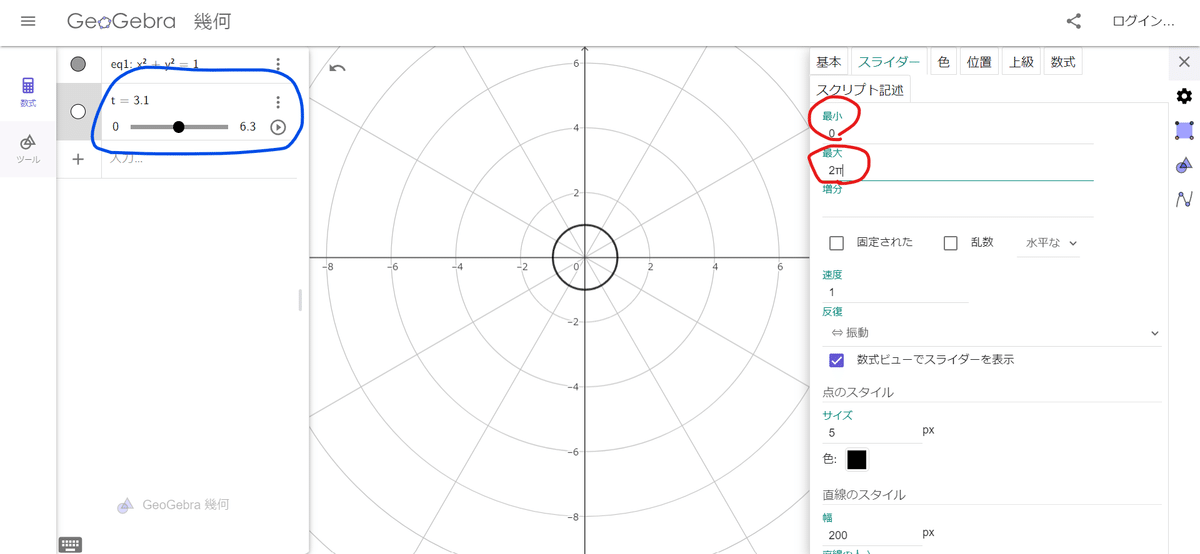
すると上図の左側のように「スライダー」が現れて、tの値を調節できるようになるよ!
パラメータも用意できたことだし、次は動点Pを用意しよう。
入力欄に以下のように入力して
P=(cos(t),sin(t))色を[設定]から赤色に変えると、下のようになるよ。

動点を用意できたってことで、一旦tを動かしてPがどんな動きをするか見てみよう。
スライダーの▶を選択するとtが自動で動かせるよ!
動かしたらわかると思うんだけど、この動点の動きってちょっとおかしいよね。
tの値の変化が"振動"しているから一周した後そのまま進まずに逆走しちゃうんだね。
じゃあtの値を[振動]から[増加]に変えてあげよう。
さっきのスライダーの設定画面から
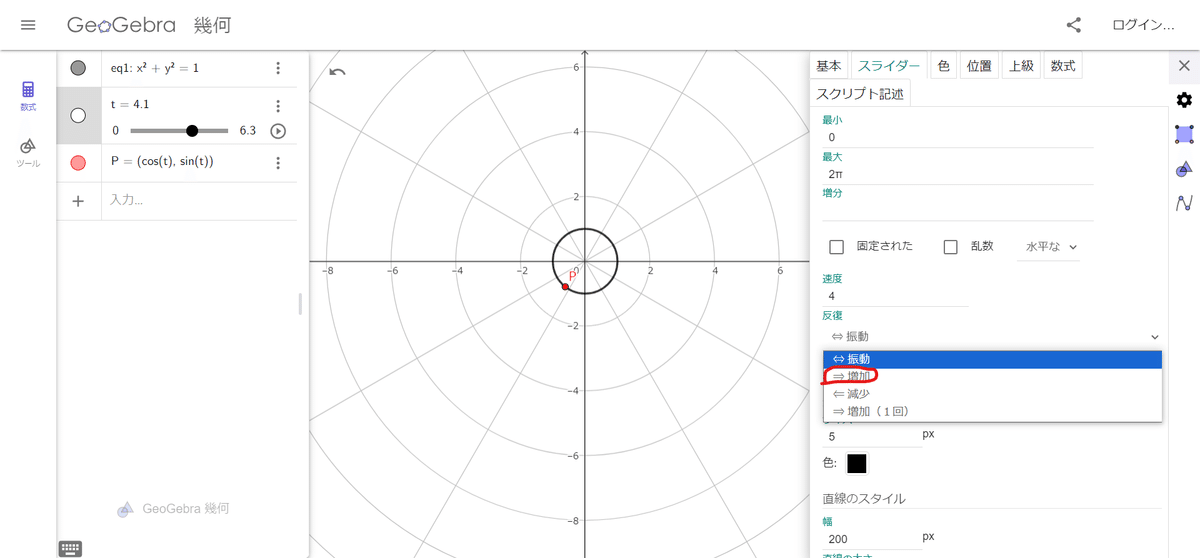
下図のように[増加]を選ぶとずっと動点がぐるぐる回るようになるね!
それじゃあ準備も整ったってことでベクトルと絡めて遊んでみよう。
まず点Pの位置ベクトル$${\bm{p}}$$を描画しよう。
これは簡単にできるね。Vectorコマンドの引数は"点"だから、点Pをそのまま書けばいいね。
p=Vector(P)色を赤に変えると次のようになると思う。

じゃあ次に速度ベクトル$${\bm{v}}$$を描画しよう。
$${\bm{v}=\frac{d}{dt}\bm{p}=[-\sin t,\cos t]}$$だから、$${\bm{v}}$$が点Pの束縛ベクトルであることに注意すれば、
v=Vector(P,(-sin(t),cos(t))+P)と入力してあげればいいね。この場合Vectorコマンドの引数の形は
Vector(始点,終点)となるから、終点=変化分の座標(v)+始点(P)にしないといけないんだね。
これも色を青に変えると次のようになると思う。

この図から視覚的に位置ベクトルと速度ベクトルが直交することがわかるね。
じゃあ最後に加速度ベクトル$${\bm{a}}$$を描画しよう。
$${\bm{a}=\frac{d}{dt}\bm{v}=[-\cos t,-\sin t]\hspace{1mm}(=-\bm{p})}$$
であることと、速度ベクトルと同様点Pの束縛ベクトルであることに注意してあげれば
a=Vector(P,(-cos(t),-sin(t))+P)もしくは
a=Vector(P,(-cos(t),-P+P)より
a=Vector(P,(-cos(t),0)と入力してあげればいいね。
見やすくするために色を緑を変えてあげると次のようになると思う。

この図から加速度ベクトルと速度ベクトルは直交し、位置ベクトルと向きが反対であることが視覚的に理解できるね!
とはいえこんなに小さい円じゃ矢印がごちゃごちゃしていて見にくいよね。
ということでこの円の半径を大きくしてあげよう!
これは半径をパラメータrで管理すればいいんだね。
先ほどと同様に入力欄にr=1と入力しよう。
そしたら最初の等式を次のように変えて
eq1: x^2+y^2=r^2動点Pも下のように変えてみよう。
P=r(cos(t),sin(t))そして、速度ベクトルと加速度ベクトルもそれぞれ
v=Vector(P,r (-sin(t),cos(t))+P)a=Vector(P,r (-cos(t),-sin(t))+P)と変えてあげれば

こんな感じで円の大きさも調節出来て見やすくなるね。
ただこのままだとrが負の値を取ってしまうよね。
こういうときはrのスライダーの設定で最小値を0にしてあげよう。

こうすればrが負の値を取ることはないね!
あとはt,rを同時に動かして遊んでみよう!それぞれの増加のスピードを変えてみるのも楽しいよ!
終わりに
ミケ:今日はGeoGebraを使ってたくさん遊んだな~。
マロ:お、ミケ何してるの?
ミケ:お~、マロ!ちょうどいいところに来たね!今ベクトルで遊んでるんだよ!
マロ:それは面白そうだねー。教えて教えて!
それから二匹は飼い主さんが返ってくるまでの数時間をGeoGebraに費やしました。
等速円運動のGeoGebraのファイルは公開します!よかったらどうぞ!
誤字脱字や間違いの指摘、質問や感想等は遠慮なくどうぞ!
ーミケー
