金融データと神経細胞の活動電位の類似性について：ルルコフ写像のもたらす可能性

金融データの変動は恐ろしく複雑で予測不能に見える。

その結果、トレーダーの中には、２種類のタイプの人間が生まれた。
一方は、「金融データは複雑すぎるから、確率論的にしか捉えることはできない」と考える人。
もう一方は、「複雑に見える金融データの中にも、我々が気づいていない決定論的な法則が存在するはずだ」と考える人。

同じようなタイプ分けが、量子論を論じる物理学者の間にも生じている。
つまりこの問題は極めて哲学的関心をそそるものであり、だからこそ私も金融時系列データ分析に惹かれるのだ。

金融データの変動と神経細胞の活動電位の挙動は非常に似ている。

1950年1月以降のダウ・ジョーンズ株価と日次リターン（対数スケール）。

この細胞外波形は、未知の数のニューロンから発生した複数の異なる活動電位を示している。データはゼブラフィンチの前脳核LMANからガラスコート白金イリジウム電極で記録した。

それはどちらも、ミクロなエージェント同士が相互に影響を及ぼし合う巨大なネットワークシステムという点で共通しているからだ。（この点については、以前の記事でも詳述した）

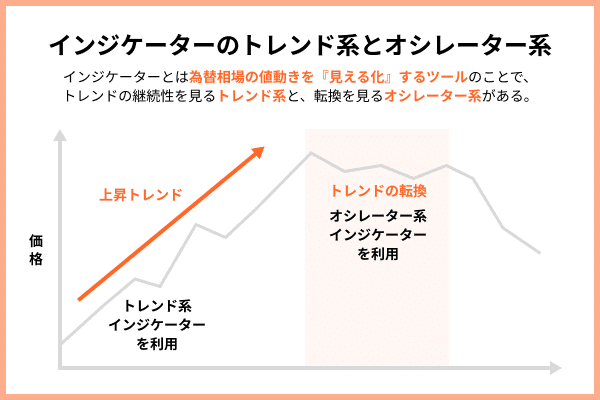
データの特徴としては、周期的な変動を繰り返す時期と、１つの方向に大きく触れる時期が分かれるということだ。
FXでは、この違いを「トレンド系」と「オシレータ系」という相場環境の違いとして説明する。

従来の神経活動のモデリング方法では、Hodgkin-Huxley方程式として知られる４元連立微分方程式を解かないと解を導出できなかった。連立微分方程式の解という意味では、アインシュタインの重力方程式のシュヴァルツシルト解を１つひねり出すだけでも一苦労だというのに、ニューロンが形成するネットワークとなると、規模が大きくなるにつれてほぼ解を導くのが不可能なほどに複雑化してしまう。（注：フィッツヒュー・南雲 (FitzHugh-Nagumo) 方程式という簡素化バージョンもあるらしい）

そこで2001年にカリフォルニア大教授のNikolai F. Rulkovによって提案されたのが、以下のルルコフ写像(Rulkov Map)。

複雑にしか表現できなかったはずの神経の活動電位に対して、極めて類似の性質を示すシンプルな式を考案した。それが以下。

ルルコフ写像の基本式

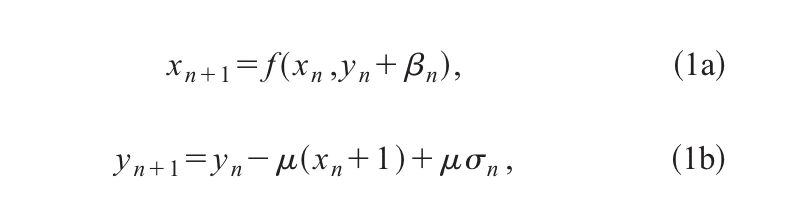
ルルコフ写像は、中心となる２つの内生的な変数（x, y）と、３つの外生的な変数（μ、β、δ）からなる。

• x : 早い変数。実際のデータの変動に該当する。

• y: 遅い変数。ゆっくりとしか変化しないが、金融データでは「記憶」に該当する。

ちなみにyが遅い変数にするために、通常は変数μを0.001くらいの小さな数に設定するように指示される。

その他の変数であるβ、δは、神経細胞に対して外部から与えられる電気刺激の影響を式に取り入れるための項である。外部電流Iが与えられる時の影響の大きさを決めるためのパラメータとして定義される。

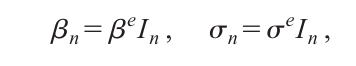
ここで忘れてはいけないのが、中心的な役割を担うf(x, y)の定義。

αというパラメータが重要な役割を果たしていることがわかる。
ちなみに2.0＜α＜4.0の時にxは周期的な振る舞いを示し、4.0<α＜5.0の時にカオスな振る舞いを示す。

こうして定義されたルルコフ写像は、実際の神経活動を驚くほど模倣するような振る舞いを示す。

例えばこんな感じ。

f(x, y)の主要なパラメータであるαの値を変えた際のルルコフ写像の振る舞い

こうしてできるルルコフ写像を使ってパラメータをいじっていると、以下のα-δパラメータ平面を使って、「一定の値で動かない時」と「スパイクが出る時」と「スパイクがバーストする時」の３つのレジームを特定することができる。

これでなんとなく、トレンドとオシレータの、「相場レジーム」の違いが説明できそうな気がしてくる。

ここまででも十分面白いのだが、ここからがさらに面白い。

ここで主要な役割を担うのが、外生変数βとδである。
例えば、同じパルス刺激を与えられた時に、βとδが違うだけで全く異なる挙動を示すことがわかる。

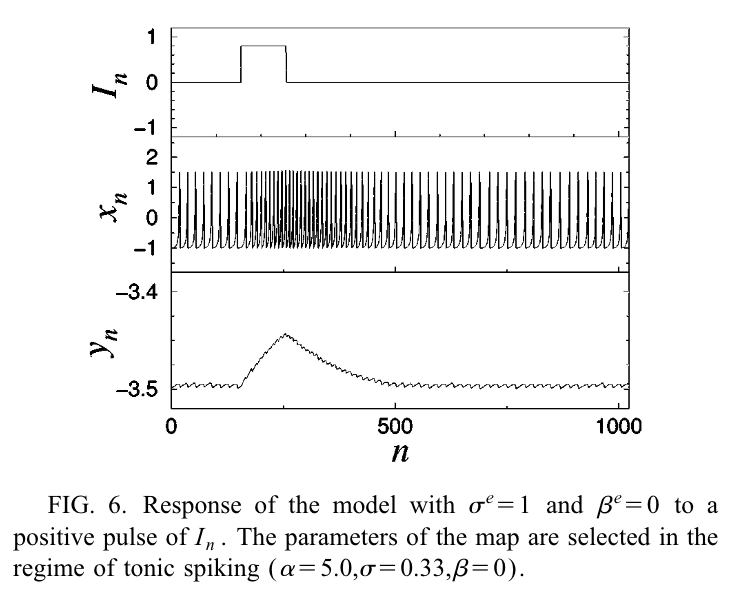
上の状況では、電位が加わることでyがぐっと持ち上がっている一方で、下の状況では、電位が加わることで一旦yがガクンと下がり、その後急に思い出したかのようにぐっと上がり、そこからまたじわじわと下がっていく。

これを見ると、経済指標発表の時のFXチャートの動きを思い出す。

経済指標が発表されると、大抵相場は大きく動くのだが、ポジティブな結果が必ずしも相場の上昇につながるとは限らない。むしろ逆に、ポジティブな結果が出たはずなのに何故か相場がガクンと下がる、みたいなことがかなり頻繁に起きる。
ニュースではよく、「ポジティブな結果はすでに市場に織り込み済みで、その期待を上回れなかったから下がる」みたいな説明がされるが、それは暫定的なディスクールに過ぎないと思う。

私は「FXに理論があるとしたら、それはどのような理論的枠組みか？」というのを去年夏くらいからずっと考えてきたが、その時にぶつかる壁は決まって、

• 経済指標の発表や要人発言、あるいは為替介入による突発的な動き

• ある特定の価格の心理学的ラインに迫ったときの動き（160円で跳ね返るなど）

• 他の経済指標（例えば、ドル円にとっての米長期金利）からもたらされる影響

の３つをどのように理論に取り入れるべきか、というものだった。

ルルコフ写像のモデルでは、これらを「外部から加えられる電位」として扱える。つまり、外生変数βとδをうまく設計し、場合によってはこれらの変数を介して２つの主体間でキャッチボールを行うことで、上記３つの要素を自然にモデルの中に取り入れることができる。

応用上重要になってくるのは、他の経済指標との関連性の部分だが、そのためにはルルコフ写像を以下のように拡張する必要がある。

その上で、外生変数βとδを、異なるxi, yi同士で「キャッチボール」できるように変形する。

ドル円相場と日米金利差は、以下のような相関関係を示しているが、将来的な望みとしては上記のモデルによって下記のようなグラフを導き出したいとところだ。

ちなみに2022年に発表された先行研究として、すでに金融データへのルルコフ写像の応用は行われており、その結果、従来の金融時系列データ分析のスタンダートであるGARCHモデルと遜色ない予測結果を生み出すことができているようだ。

Financial markets’ deterministic aspects modeled by a low-dimensional equation

今後の展望としては、
金融時系列データの中で、外生変数βとδをどのように設計していくべきか
が課題になってくるに違いない。

うまくいけば、驚くほど精度の高い予測モデルが開発される可能性がある。

金融時系列データは、あたかも生物のような振る舞いを示す点が魅力だが、それがこのような形で徐々に明らかになっていくのが楽しい。

後記：
実際にrulkov mapをプログラムしたところ、下記パラメータでそれっぽいドル円チャートを擬似的に生成できた。鍵となるのは、パルスの回数。
iteration10000回に対して、パルス1000回でようやく本物らしさが出てきた。

rulkov mapによって擬似的に生成したドル円チャート

これをみると、「パルス」がいかにチャートにとって重要な役割を果たしているかがわかる。つまり、正確な予測をするためには、まずはパルスの存在を観測し、それがもたらす影響を推定するという作業が必要になる。

実際のドル円チャート

パルス100回だと全然それっぽくない

ちなみにランダムウォークでやるとこんな感じ。トレンドもへったくれもあったものではない。これをみると、株価チャートは明らかにランダムウォークではないことがわかる

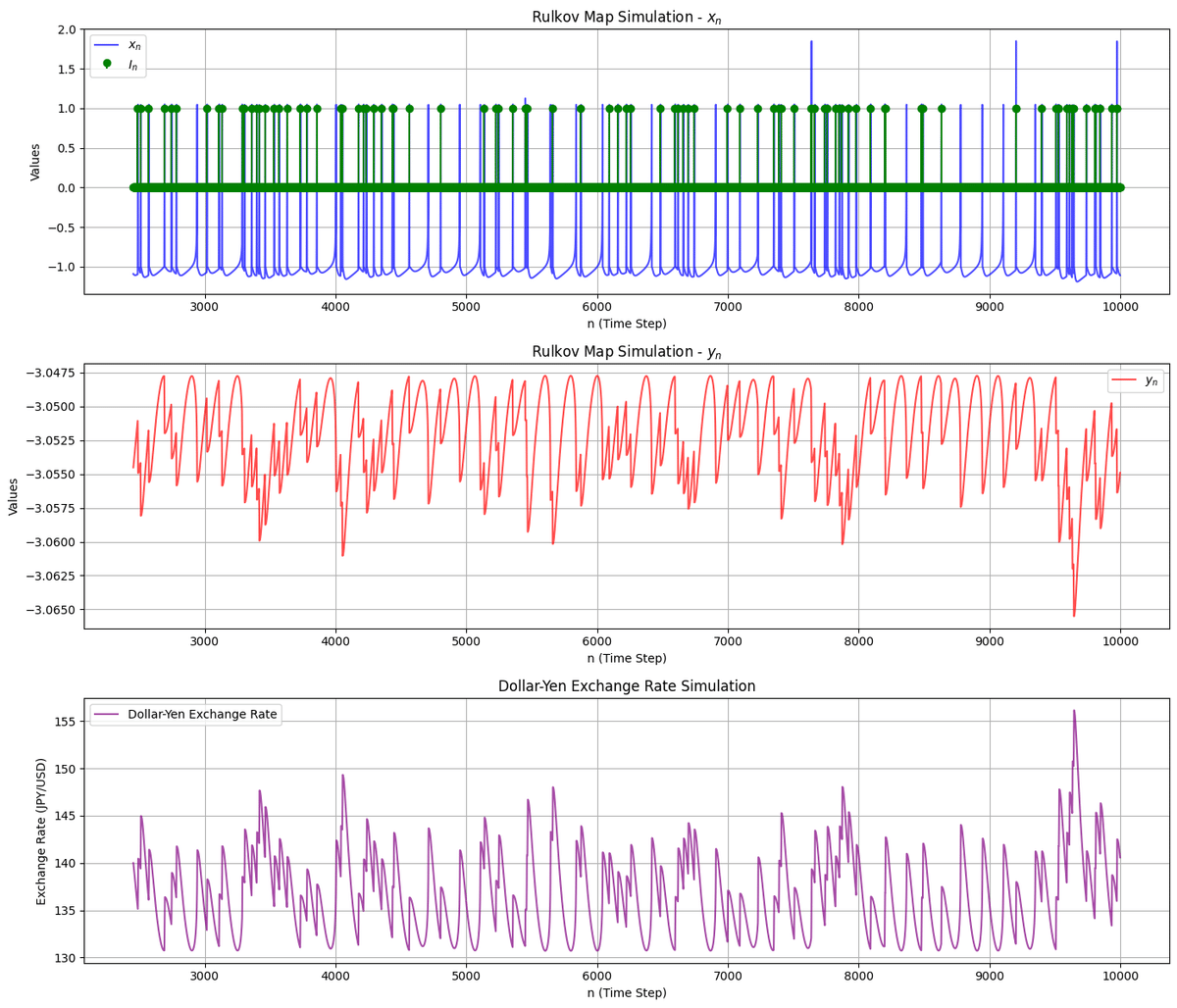
上記の実験を踏まえると、「株価にはランダムウォークに見える部分があるがそのランダムネスは実際にはパルス波（外部要因）に起因するものだ」と推定される。その場合、外部要因をファンダメンタルズである程度正確に把握することができれば、ランダムネスを可能な限り減らして予測することが可能なはずだ。

import numpy as np
import matplotlib.pyplot as plt
import ipywidgets as widgets
from ipywidgets import interact, FloatSlider, IntRangeSlider
from IPython.display import display

def f(x, y, alpha):
    if x <= 0:
        return alpha / (1 - x) + y
    elif 0 < x < alpha + y:
        return alpha + y
    else:
        return -1

def generate_pulse(n, pulse_count):
    pulses = np.zeros(n)
    pulse_times = np.random.choice(n, pulse_count, replace=False)
    pulses[pulse_times] = 1
    return pulses

def rulkov_map(alpha, beta_star, delta_star, mu, num_iterations, initial_conditions, pulse_count):
    x = np.zeros(num_iterations)
    y = np.zeros(num_iterations)
    beta = np.zeros(num_iterations)
    delta = np.zeros(num_iterations)
    I = generate_pulse(num_iterations, pulse_count)
    x[0], y[0] = initial_conditions
    
    for n in range(num_iterations - 1):
        beta[n] = beta_star * I[n]
        delta[n] = delta_star * I[n]
        x[n+1] = f(x[n], y[n] + beta[n], alpha)
        y[n+1] = y[n] - mu * (x[n+1] + 1) + mu * delta[n]
        
    return x, y, I

def compute_dollar_yen_chart(log_returns, start_price=140):
    prices = [start_price]
    for r in log_returns:
        prices.append(prices[-1] * np.exp(r))
    return np.array(prices)

def plot_rulkov_map_and_dollar_yen(alpha, beta_star, delta_star, pulse_count, iteration_range):
    # Parameters
    mu = 0.001
    num_iterations = 10000
    initial_conditions = (0, 0)
    
    # Generate the Rulkov map
    x, y, I = rulkov_map(alpha, beta_star, delta_star, mu, num_iterations, initial_conditions, pulse_count)
    
    # Define the range for plotting
    start, end = iteration_range
    
    # Generate log returns and dollar-yen chart
    log_returns = (x / 100.0) + 0.01
    prices = compute_dollar_yen_chart(log_returns[start:end], start_price=140)
    
    # Plotting the results
    fig, (ax1, ax2, ax3) = plt.subplots(3, 1, figsize=(14, 12))
    
    ax1.plot(range(start, end), x[start:end], alpha=0.7, color='blue', label='$x_n$')
    ax1.stem(range(start, end), I[start:end], linefmt='g-', markerfmt='go', basefmt=' ', label='$I_n$')
    ax1.set_title('Rulkov Map Simulation - $x_n$')
    ax1.set_xlabel('n (Time Step)')
    ax1.set_ylabel('Values')
    ax1.legend()
    ax1.grid(True)
    
    ax2.plot(range(start, end), y[start:end], alpha=0.7, color='red', label='$y_n$')
    ax2.set_title('Rulkov Map Simulation - $y_n$')
    ax2.set_xlabel('n (Time Step)')
    ax2.set_ylabel('Values')
    ax2.legend()
    ax2.grid(True)
    
    ax3.plot(range(start, end), prices[:-1], alpha=0.7, color='purple', label='Dollar-Yen Exchange Rate')
    ax3.set_title('Dollar-Yen Exchange Rate Simulation')
    ax3.set_xlabel('n (Time Step)')
    ax3.set_ylabel('Exchange Rate (JPY/USD)')
    ax3.legend()
    ax3.grid(True)
    
    plt.tight_layout()
    plt.show()

# Create interactive widgets
alpha_slider = FloatSlider(min=1, max=5, step=0.1, value=2, description='alpha')
beta_star_slider = FloatSlider(min=-1, max=1, step=0.1, value=0, description='beta*')
delta_star_slider = FloatSlider(min=-1, max=1, step=0.1, value=0, description='delta*')
pulse_count_slider = widgets.IntSlider(min=1, max=1000, step=1, value=1000, description='Pulse Count')
iteration_range_slider = IntRangeSlider(min=0, max=10000, step=1, value=[0, 10000], description='Iteration Range')

# Create interactive plot
interactive_plot = interact(
    plot_rulkov_map_and_dollar_yen, 
    alpha=alpha_slider, 
    beta_star=beta_star_slider, 
    delta_star=delta_star_slider, 
    pulse_count=pulse_count_slider, 
    iteration_range=iteration_range_slider
)
display(interactive_plot)