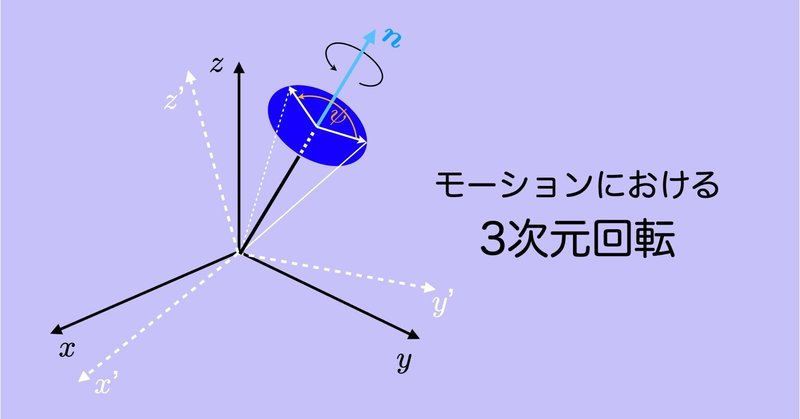
モーションにおける3次元回転 #6 〜クォータニオンの導入〜
単位クォータニオンとオイラーパラメータ
クォータニオン(quaternion)は四元数(しげんすう)とも呼ばれ,アイルランドの数学者ハミルトンが1843年に,現在ウィリアム・ローアン・ハミルトン橋と呼ばれている橋を歩いているときに,ひらめき,そのアイデア(下記の式)を橋にナイフで刻んだと伝えられている.

なお,回転を含めた2次元平面の幾何学を記述する複素数が,4次元へ拡張されたのものがクォータニオンで,さらにその大きさが1を満たす特別な単位クォータニオン(unit quaternion)が3次元回転の回転パラメータとして利用できる.
この単位クォータニオンは回転パラメータ,すなわち回転行列を表現するパラメータ(他にオイラー角などがある)として利用されることが多く,スマートフォンなどにも使用されている最近のIMU(慣性センサ,モーションセンサ)のほとんどがこの単位クォータニオンを出力する.したがってIMUを使いこなそうと思うなら,単位クォータニオンの演算に親しむ必要があるだろう.
ただし,ここで注意が必要で,世の中で単にクォータニオンと呼ばれているもののほとんどが,実際には単位クォータニオンであることが多く,区別を意識しておくべきである.
なお,単位クォータニオンと前章まで述べてきたオイラーパラメータ(Euler parameters)は数学的に等価であるが,ハミルトンがクォータニオンを発見したときとほぼ同時代に,今日オイラーパラメータと呼ばれているこの回転パラメータも導出されている.ただし,このオイラーパラメータを発見したのは,オイラーではなく,実際にはロドリゲスがこれを発見したとされている.一方,実はロドリゲスの式は,前章までに述べてきた,オイラー角,オイラーの定理,オイラーの公式などを導出したLeonhard Eulerが導いている(参考文献1参照).
オイラーパラメータ
前章までにオイラーが発見したロドリゲスの式によって,回転軸を表す単位ベクトル$${\bm{n}}$$と回転角$${\psi}$$で回転行列を表すことができることを示してきたが,ロドリゲスは次のような4つの変数で表すオイラパラメータ$${\bm{e}}$$を考えた.
$$
\bm{e}=\begin{bmatrix}
\cos \frac{\psi}{2} \\ \bm{n}\sin \frac{\psi}{2}
\end{bmatrix}=
\begin{bmatrix}
\cos \frac{\psi}{2} \\ n_1 \sin \frac{\psi}{2} \\ n_2 \sin \frac{\psi}{2} \\ n_3 \sin \frac{\psi}{2}
\end{bmatrix}
=\begin{bmatrix}
e_0\\e_1\\e_2\\e_3
\end{bmatrix}
=\begin{bmatrix}
e_0\\ \bm{\epsilon}
\end{bmatrix}
$$
ここで,$${e_0}$$はスカラー部(scalar part),$${\bm{\epsilon}=[e_1~e_2~e_3]^T}$$はベクトル部(vector part)と呼ばれ,$${e_0}$$が回転角と,$${\bm{\epsilon}}$$が回転軸と関係している.また,$${\bm{n}}$$が大きさ1の単位ベクトルであるので,
$$
||\bm{e}|| = e_0^2+e_1^2+e_2^2+e_3^2 = 1\\
$$
が成り立ち,半径が1の単位球面を満たしいてる.
前述のように,オイラーパラメータ$${\bm{e}}$$は,今後議論する単位クォータニオン$${\bm{q}}$$と等価であるが,クォータニオンの性質を利用すると,クォータニオン積など多くの演算が成り立ち便利である.そこで以後,クォータニオンとしての性質に注目する.
クォータニオン
単位クォータニオンについて述べる前に,まずクォータニオンの性質についてまとめておく.クォータニオンは
$$
\bm{q}=q_0+q_1 i+ q_2 j + q_3 k
$$
のように複素数の拡張として表される.ここでの「和」$${+}$$は足すという加算の意味ではなく,複素数(例:$${5+3i}$$と記述する)と同様に形式的に4つの要素の集合を表していることに注意されたい.
さて,以後のクォータニオンの計算を考えると,クォータニオン$${\bm{q}}$$を先に示したオイラーパラメータ$${\bm{e}}$$と同様に,行列表示
$$
\bm{q}
=\begin{bmatrix}
q_0\\q_1\\q_2\\q_3
\end{bmatrix}
=\begin{bmatrix}
q_0\\ \bm{v}
\end{bmatrix}
$$
するほうが,コンピュテーション的に,また代数的表現の観点から都合が良いので,以後,このような表記法を多く使用することになる.
なお,前述の$${+}$$は形式和で,クォータニオンの要素の順番に意味はないため,コンピュータグラフィックスなどの一部では$${[\bm{v}^T~q_0]^T=[q_1~q_2~q_3~q_0]^T}$$の順番で記述することもあるが,本稿ではスカラ部,ベクトル部の順番で表記する.また,情報を共有するなら,できるだけこの順番を使用するほうが懸命である.
クォータニオンは複素数の拡張であるので,以下のような性質が記号$${i,j,k}$$に対して成り立ち,
$$
i^2+j^2+k^2=ijk=-1,\\
jk=i,~ki=j,~ij=k,\\
kj=-i,~ ik=-j,~ji=-k
$$
$${i,j,k}$$のそれぞれは虚数単位の性質を持つ.
クォータニオン$${\bm{q}=q_0+q_1 i+q_2 j+q_3 k, ~\bm{p}=p_0+p_1 i+p_2 j + p_3 k}$$に対するクォータニオン同士の積は
$$
\bm{qp} = (q_0+q_1 i+q_2 j+q_3 k)(p_0+p_1 i+p_2 j + p_3 k)
\\=
q_0 p_0 - q_1 p_1 - q_2 p_2 - q_3 p_3\\
+(q_0 p_1 + q_1 p_0 + q_2 p_3 - q_3 p_2)i\\
+(q_0 p_2 - q_1 p_3 + q_2 p_0 + q_3 p_1)j\\
+(q_0 p_3 + q_1 p_2 - q_2 p_1 + q_3 p_0)k
\\=
\begin{bmatrix}
q_0 & -q_1 & -q_2 & -q_3\\
q_1 & q_0 & -q_3 & q_2\\
q_2 & q_3 & q_0 & -q_1\\
q_3 & -q_2 & q_1 & q_0
\end{bmatrix}
\begin{bmatrix}
p_0\\
p_1\\
p_2\\
p_3
\end{bmatrix}
\\=
\begin{bmatrix}
p_0 & -p_1 & -p_2 & -p_3\\
p_1 & p_0 & p_3 & -p_2\\
p_2 & -p_3 & p_0 & p_1\\
p_3 & p_2 & -p_1 & p_0
\end{bmatrix}
\begin{bmatrix}
q_0\\
q_1\\
q_2\\
q_3
\end{bmatrix}
$$
と書くことができ,これをクォータニオン積(quaternion product)と呼ぶ.ここで,3,4行目の行列部分の符号が異なっていることからもわかるが,
$$
\bm{qp} \neq \bm{pq}
$$
のようにクォータニオン積では可換則が成り立たない.
また,クォータニオンは複素数の拡張であるから,共役クォータニオン(conjugate quaternion)$${\bm{q}^{*}}$$を
$$
\bm{q}^{*}=q_0-q_1 - q_2 j - q_3 k=q_0 - \bm{v} = \begin{bmatrix}
q_0\\-q_1\\-q_2\\-q_3
\end{bmatrix}
$$
と定義すると,クォータニオンのノルム(norm)も次のように
$$
||\bm{q}|| = \sqrt{\bm{q} \bm{q}^{*}}= \sqrt{\bm{q}^{*}\bm{q}} = \sqrt{q_0^2 + q_1^2 + q_2^2 + q_3^2}
$$
と定義でき,クォータニオンの逆元(逆クォータニオン)(reciprocal)も
$$
q^{-1} = \frac{q^{*}}{||q||^2}
$$
のように定義できる.これはベクトルにはない性質である.
繰り返しになるが,2次元平面全体を記述する複素数が4次元に拡張されたのがクォータニオンで,クォータニオン自体は3次元回転を記述するわけではない.また,2次元複素平面で単位円を考えるとオイラーの公式
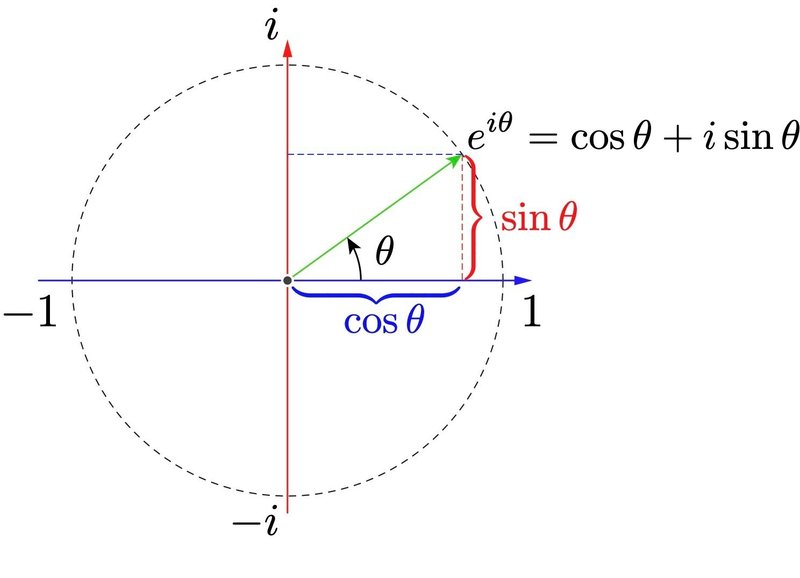
$${e^{i\theta}=\cos \theta + i \sin \theta}$$
のように平面の回転を1自由度で表現できるように,4次元のクォータニオンに単位球面の拘束($${||\bm{q}||=1}$$)を与えることで,すなわち単位クォータニオンによって,3次元における回転を記述できることに注意が必要である.単位クォータニオンによる表現は4変数で記述され冗長性があるように思えるが,単位球面の拘束によって実質3次元空間の回転を3自由度で表現している.
クォータニオンについては,この程度にとどめて,次章から単位クォータニオンの性質や演算ついて述べていく.
なお,3次元の回転行列の表現方法の代表であるオイラー角と比較した際に,特異点が発生しないことが単位クォータニオンの長所として語られることが多いが,むしろ,次章から述べる単位クォータニオンによって回転軸と回転角という物理的意味が直感的に捉えやすいことがバイオメカニクスの解析では大きなメリットとなり,回転パラメータである単位クォータニオン同士の演算が解析の武器となる.オイラー角同士ではこのような演算はできないし,その角度に明確な物理的意味はない.
参考文献
1.ロボットモーション(岩波講座ロボット学2),内山勝・中村仁彦著,岩波出版

【解析・受託開発について】
スポーツセンシングでは,豊富な知見を持つ,研究者や各種エンジニアが研究・開発のお手伝いをしております.研究・開発でお困りの方は,ぜひスポーツセンシングにご相談ください.
【例】
・データ解析の代行
・受託開発
(ハードウェア、組込みソフトウェア、PC/モバイルアプリ)
・測定システム構築に関するコンサルティング など
その他,幅広い分野をカバーしておりますので,まずはお気軽にお問い合わせください.
株式会社スポーツセンシング
【ホームページ】sports-sensing.com
【Facebook】sports.sensing
【Twitter】Sports_Sensing
【メール】support@sports-sensing.com
