
動かして学ぶバイオメカニクス #17 〜動力伝達の可視化〜
全身に作用する力とトルクが力学的なエネルギーの流れをもたらすことを前章で示した.トルクと異なり,実質的な運動の効果はこのエネルギーの変化のほうが観察しやすい.ここでは,それらを可視化する方法を示すが,この方法は一例に過ぎず,示し方は工夫次第だ.
230501 訂正: 関節に作用するトルクに起因し,その関節$${i}$$から近位側$${i-1}$$に流入するエネルギーの時間変化(パワー)$${-\bm{\tau}_{i}^T \bm{\omega}_{i-1}}$$を計算する関数power_tau_parent()のコードにおける座標変換に誤りがあった.使用した関数と計算の訂正を行った.お詫び申し上げる.
はじめに
この章では,第16章で述べた力学的エネルギーの時間変化を可視化するコードを示していきたい.次章で運動中の力ベクトルと速度ベクトル,さらにはインピーダンスという観点で効率について考えていく予定でる.
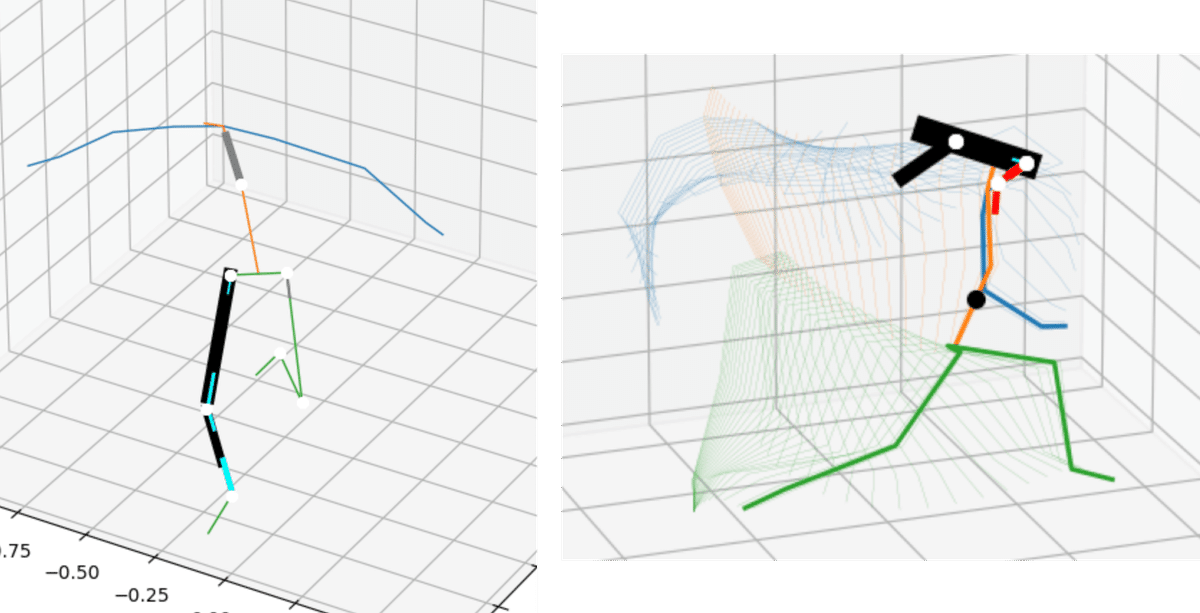
黒・グレー:関節に作用する力由来のエネルギーの流れ(黒:正,グレー:負)
赤・水色:関節に作用するトルク由来のエネルギーの流れ(赤:正,青:負)
図1は飛び降り動作(左)や投球動作(右)の力学的エネルギーの時間変化,すなわち力学的エネルギーの流れを可視化した例である.コードを後ほど示すので,実際に動かしていただければと思う.
確認した動作環境とコードについて
いつものように,以下のGoogle ColaboratoryのリンクからブラウザでPythonコードを実行できる.なお,ログインするためには,Googleアカウントが必要となるので注意をされたい.
また,使用するモーションキャプチャのサンプルデータは2種類あり,図1左の飛び降り動作として(sample_optitrack_221027.csv)とフォースプレートのデータ(sample_fp_221027.csv),図1右の投球動作のモーションキャプチャのデータ(sample_optitrack_sec15.csv)は,このリンクからダウンロードして,Google Driveをマウントし,マウントしたドライブにそれらをコピーしてご使用いただきたい.すでにダウンロ度済みの方は,再度ダウンロードする必要はない.
また,Google ColaboratoryやGoogle Driveの使用方法は,
を参照されたい.
ここでのコードは,JupyterLab(デスクトップアプリ),Google Colaboratoryで検証したが,とくにグラフィックスの表示結果やコードは,その二つでも若干動作が異なる.動作させるPython環境に依存し,少々修正が必要となるかも知れない.とりあえずJuputerLabのアプリやGoogle Colabratoryで確認したが,環境によってグラフィックスのコードの調整をお願いしたい.ここで示したコードは,JupyterLabで動作するが,Colabでは若干修正している.
なお,環境によっては,
ax.set_aspect('equal')によって,xyz軸間のスケール比(アスペクト比)を調整し,軸間の長さのスケールを等しくすることができるが,Colabではこれが機能しないため,描画範囲をax.set_xlim(), ax.set_ylim(), ax.set_zlim()で指定している.筆者の力不足で申し訳ないが,適宜環境に合わせて調整をしていただきたい.
スティックピクチャにエネルギーの流れを示す
使用する関数は第15章
からさらに若干修正している.ここでは訂正部分と,主として新しく定義した関数を以下に示す.
パッケージの読み込み
import seaborn as snsグラフを描画する際にMatplotlibが多く使用されるが,SeabornはMatplotlibの機能をより美しく,より簡単に実現するための可視化ライブラリで,Matplotlibベースで作られている.このパッケージは力学的エネルギーの時間変化(エネルギーの流れ)を可視化する際の「ヒートマップ」を使用する上で必要となる.
もし,seabornを上記のようにimportしても,「Seabornがインストールされていない場合」は,下記のコマンドをターミナルなどで実行し,seabornパッケージをインストールする.
pip install seaborn# 環境によってはpip3
# Jupyterなどでは ターミナルを使用せず,"!pip install seaborn" とすることで,インストールできる
# Google Colabでは不要などでインストールが可能だが,環境に応じて必要なコマンドでインストールすること.
クラス・関数の修正
また,今回BodyLinkクラスのインスタンス変数として,その部位から見た親の部位の情報を取得するため,parent_val を加えた.
##########################################################
# class BodyLink
##########################################################
class BodyLink:
def __init__(self, l_id:int, name:str, m_type:str, mass_ratio:float, cg_ratio:float):
# linkの親の変数(トルク由来の力学的エネルギーの時間微分を計算する際に必要) # 23.01.24加筆
self.parent_val = None
##########################################################
# 親子・姉妹関係
##########################################################
# トルク由来の仕事率を計算する際,関節の親側に寄与する仕事率を計算する際に,親の部位の情報が必要
def set_parent(self, parent_val):
self.parent_val = parent_valこれは,前章
の図11近辺の式で示しているように,部位1と2の両方の系全体のエネルギー変化は
$$
\dot{E}_1 + \dot{E}_2 = \bm{f}_{1}^T \dot{\bm{x}}_1 + \bm{\tau}_1^T \bm{\omega}_1 + \bm{\tau}_2^T (\bm{\omega}_2 - \bm{\omega}_1)
$$

に示されているが,関節2に作用するトルク$${\bm{\tau}_2}$$は,関節2が所属する自身の部位2と,親の部位1の両方に作用する.そこで,部位2へは$${\bm{\tau}_2^T \bm{\omega}_2}$$だけエネルギーが流れ,部位1へは$${-\bm{\tau}_2^T \bm{\omega}_1}$$だけエネルギーが流れる(図2).このとき,親へのエネルギーの流れを示すために,つまり関節2から関節1方向に流れをベクトル(線分)で示すために,自身からみた親の部位の情報を取得する必要があり,下記の配列と関数を準備した.
これまでのコードでは,クラスBodyLinkに自身から見た子供と遠位端の情報としてのインスタンス変数(self.child_val, self.distal_val)にしか格納していなかったためで,親の部位の情報を取得するためparent_val を加えた.
# 各リンクの親の部位の情報を格納.b_linkの parent_valに追記
parent_list = [
[1,0], [2,1], [3,2], [4,2], [5,4], [6,5], [7,2],
[8,7], [9,8], [10,1], [11,10], [12,11], [13,1],
[14,13], [15,14]]この parent_list は,parent_val にデータを加えるために必要な親子関係の情報の配列で,後ほど使用する.
一方,関節2に作用する力$${\bm{f}_2}$$は,部位1と2間のエネルギーの伝達を担う.これらの部位が動けば,部位間でエネルギーの移動が行われる(図3).ここでは,これを黒線またはグレーの矢印で示す.黒は正の値で,グレーは負の値を示す.たとえばこれが正のときは親の部位から自身のリンクへの移動を示し,負の場合は自身の部位から親の部位への移動を示す.負の場合は親方向を向く矢印(線分)で示す方法も考えられるが,ここでは先程示したトルクによるエネルギーの流れの可視化との整合性を考えて,線分(矢印)の方向は常に遠位端方向を向き,色で符号を区別することとした.これは,適宜,読者の方で変更していただければ良い.

なお,この他の修正として,下記のset_frame(),set_frame_link(),diff_joint_vec(),frame_method1(), frame_method2()関数の引数のとり方を修正した.
# 23.01.23 訂正
# bodylinkと部位のl_idを指定し,各linkの姿勢行列を計算し,インスタンスrotに格納
def set_frame(body_link, l_id, frame_dict):
method1 = [1, 2, 3, 5, 6, 8, 9]
method2 = [4, 7, 10, 11, 12, 13, 14, 15]
f_dict = frame_dict[l_id]
if any(l_id == elem for elem in method1):
body_link[l_id].rot = frame_method1(body_link, f_dict[0], f_dict[1], f_dict[2], f_dict[3])
elif any(l_id == elem for elem in method2):
body_link[l_id].rot = frame_method2(body_link, f_dict[0], f_dict[1], f_dict[2], l_id)
else:
print('error')
def set_frame_link(body_link, l_id_list, frame_dict):
for n in l_id_list:
set_frame(body_link, n, frame_dict)# 23.01.23 訂正
# 2つの位置ベクトルの差分
# origin, headの順番で指定
def diff_joint_vec(body_link, j_origin_id, j_head_id):
return body_link[j_head_id].p - body_link[j_origin_id].p
# 手,前腕の座標系
# 手首の外・橈骨側マーカA,内・尺骨側マーカB を利用
# 左右で以下のマーカの順番が異なるので注意.右はRWRA, RWRBの順で指定.左はLWRB, LWRAの順で指定
# x軸:蝶番関節方向
# z:長軸,y:前後方向
# z軸は近位から遠位方向なので,右は回外,左は回内に相当
def frame_method1(body_link, j_origin_id, j_head_id, j_right_id, j_left_id):
joint_unit_axis_z = unit_vec(diff_joint_vec(body_link, j_origin_id, j_head_id))
joint_axis_x = diff_joint_vec(body_link, j_right_id, j_left_id)
joint_unit_axis_y = unit_vec(np.cross(joint_unit_axis_z, joint_axis_x))
joint_unit_axis_x = np.cross(joint_unit_axis_y, joint_unit_axis_z)
return np.array([joint_unit_axis_x, joint_unit_axis_y, joint_unit_axis_z])
# 上腕,大腿,下腿,足の座標系
# 3つの関節中心座標が計算に必要
# x軸:蝶番関節方向(伸展屈曲軸)
# z:長軸,y:前後方向
def frame_method2(body_link, j1_list, j2_list, j3_list, joint_id=4):
joint_unit_axis_z1 = unit_vec(diff_joint_vec(body_link, j1_list, j2_list)) # z1: joint1 → joint2
joint_unit_axis_z2 = unit_vec(diff_joint_vec(body_link, j2_list, j3_list)) # z2: joint2 → joint3
# 関節の構造と外積の性質から,部位によって左右軸のx軸の向きが変化する(注意:過伸展に未対応)
lst1 =[4, 7, 12, 15]
lst2 =[10, 13, 11, 14]
if any(joint_id == elem for elem in lst1):
pm = -1.
elif any(joint_id == elem for elem in lst2):
pm = 1.
joint_unit_axis_x = pm * unit_vec(np.cross(joint_unit_axis_z1, joint_unit_axis_z2))
lst3 =[4, 7, 10, 13]
lst4 =[11, 14, 12, 15]
if any(joint_id == elem for elem in lst3):
joint_unit_axis_y = np.cross(joint_unit_axis_z1, joint_unit_axis_x) # y1軸
return np.array([joint_unit_axis_x, joint_unit_axis_y, joint_unit_axis_z1])
elif any(joint_id == elem for elem in lst4):
joint_unit_axis_y = np.cross(joint_unit_axis_z2, joint_unit_axis_x) # y2軸
return np.array([joint_unit_axis_x, joint_unit_axis_y, joint_unit_axis_z2])スティックピクチャ
第15章
で示した,スティックピクチャの描画する関数を以下にまとめる.
スティックピクチャを描く関節点の順番を配列に収める.スティックピクチャは3つの線で描く.前述したように,軸のアスペクト比を調整するax.set_aspect('equal')は環境に応じて使用していただきたい.
# クラスBody_link用
upper_arm_list = [17, 6, 5, 4, 3, 7, 8, 9, 18] # 上肢の関節位置
body_list = [16, 3, 2, 1] # 頭から腰までの関節位置
lower_body_list = [19, 12,11, 10, 13, 14, 15,20] # 下肢の関節位置
# 上記で定義した関節位置のリストを利用し
# xyz3成分を出力
def joint_p_list(body_link, time, joint_list):
return np.array([body_link[num].p[time] for num in joint_list]).T
# スティックピクチャを描く関数
def stick(ax, body_link, time, lw=1, xrange=(-.2, 1.75), yrange=(-.5, 1.), zrange=(0, 2.1)):
ax.plot(*joint_p_list(body_link, time, upper_arm_list), linewidth=lw, c='C0')
ax.plot(*joint_p_list(body_link, time, body_list), linewidth=lw, c='C1')
ax.plot(*joint_p_list(body_link, time, lower_body_list), linewidth=lw, c='C2')
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')
ax.set_xlim(*xrange)
ax.set_ylim(*yrange)
ax.set_zlim(*zrange)
# ax.set_aspect('equal') # アスペクト比調整エネルギーの流れの可視化
ここでは,これまで示したスティックピクチャ関数に加えて,さらに図1で示したようなエネルギーの流れを線分で上書きする.
エネルギーの時間変化(仕事率,power)は方向の情報を含まないスカラ量である.しかし,それらの物理的意味としてエネルギーをやり取りする対象の部位が定まっているので,その符号で流れの対象としての向きが定まる.このエネルギーの流れ(伝達,流入,吸収)を示すため,流れの方向を矢印で示したいが,残念ながら3Dで矢印を綺麗に表示することがPythonではやや困難なため,ここでは単純に線分で示す.
ただし,流れの速さ(大きさ)に応じて「線分の長さ」と,「太さ」を変えていく.
なお,関節2に作用するトルク(筋力)は,図2に示したように,部位1と2にエネルギーの供給・吸収を行うため,2つの線分が必要になる.そこで,関節2(自身)から関節1(親)に向かう線分と,関節2から関節2の遠位端へ向かう線分の2つの線分でその方向を表すことにした.
なお,$${\bm{\tau}_2^T \bm{\omega}_2}$$と$${-\bm{\tau}_2^T \bm{\omega}_1}$$はそれぞれ部位2,1へのエネルギーの流れを示し,系全体のエネルギー変化は$${\bm{\tau}_2^T (\bm{\omega}_2 - \bm{\omega}_1)}$$で示される.
そこで,運動を行いながら関節角度を一定とする場合,部位1と2間の相対角度も一定となるため,$${\bm{\omega}_2 - \bm{\omega}_1}$$は小さくなり,$${\bm{\tau}_2^T (\bm{\omega}_2 - \bm{\omega}_1)}$$も小さくなる.このとき,関節を固定するためには多くのエネルギーが必要とされ,関節2から,部位1と2へ同程度のエネルギーが供給,または吸収しながら関節を固定することになる.
そこで,関節まわりで筋肉がどのような活動を行っているか理解するためには,相対的なエネルギー変化$${\bm{\tau}_2^T (\bm{\omega}_2 - \bm{\omega}_1)}$$ではこのことを観察できないため,各部位へのエネルギーの流れ$${\bm{\tau}_2^T \bm{\omega}_2}$$と$${-\bm{\tau}_2^T \bm{\omega}_1}$$を個別に計算することで現象を観察することができるだろう.
また力学的エネルギーの時間変化は正負の値を持つため,エネルギーの流れには方向があり,ここでは,図が複雑になることを避けて,色の違いで流れの向き(符号)を示すこととする.
流れの可視化のコード
力学的エネルギーの時間変化$${\bm{f}_i^T \dot{\bm{x}_i}, ~\bm{\tau}_i^T \bm{\omega}_i, ~(-\bm{\tau}_i)^T \bm{\omega}_{i-1}}$$を計算する3つの関数を以下に示す.
# 関節に作用するトルク由来の力学的エネルギー変化(power):同じ部位
def power_tau(body_link, l_id):
return dot_array(frame_to_local(body_link[l_id].rot, body_link[l_id].tau_global), body_link[l_id].w)
# 関節に作用するトルク由来の力学的エネルギー変化(power):親側の部位
# 230430 訂正
def power_tau_parent(body_link, l_id):
return dot_array(frame_to_local(body_link[l_id].parent_val.rot, body_link[l_id].tau_global), -body_link[l_id].parent_val.w)
# 関節に作用する力由来の力学的エネルギー変化(power)
def power_f(body_link, l_id, s_weight=.000001, sf=360.):
return dot_array(body_link[l_id].force, smoothing_spline(body_link[l_id].p, s_weight, sf, 1))次の関数は,これを利用しエネルギーの流れを線分で記述するため,力学的エネルギーの時間変化(power),線分の単位ベクトル,powerを正規化するために必要な最大値を計算する関数 make_power_data() である.なお,最大値による正規化によってpowerの線分の長さや太さを決定する.
この関数の引数link_num_listには配列で描画する部位を数字で与える(例えば,[4,5,6]とすることで,右上腕,右前腕,右手を指定することになる).
# link_num_listで指定した部位の
# powerのデータ, powerの最大値
# powerをスティックピクチャで可視化するため, 関節とその子供(または親)の部位の関節を結ぶ単位ベクトルを生成
def make_power_data(body_link, link_num_list, s_w=.00001, sf=360.):
# 各部位のpower
p_f_list = np.array([power_f(body_link, num, s_w, sf) for num in link_num_list])
p_tau_list = np.array([power_tau(body_link, num) for num in link_num_list])
p_tau_parent_list = np.array([power_tau_parent(body_link, num) for num in link_num_list])
# 全部位のpowerの最大値
max_pf_data = np.max(np.abs(np.ravel(p_f_list)))
max_ptau_data = np.max(np.abs(np.ravel(p_tau_list)))
max_power_data = max(max_pf_data, max_ptau_data)
# 関節とその子供の部位の関節を結ぶ単位ベクトル
uv_child_list = np.array([unit_vec(body_link[num].distal_val.p - body_link[num].p) for num in link_num_list])
uv_parent_list = np.array([unit_vec(body_link[num].parent_val.p - body_link[num].p) for num in link_num_list])
return p_f_list, p_tau_list, p_tau_parent_list, uv_child_list, uv_parent_list, max_power_data以下の関数 power_f_time_vec(), power_tau_time_vec() は,これらの関数から時間timeを指定し,powerを示す線分の両端の位置ベクトルを与える(片方は関節位置).
# time を指定し, 関節に作用する力の力学的エネルギー変化(power)と方向:unit_vecを使用し,
# powerの線分の両端の点のlistを作る
# p_f_normにはpower_f()で計算したpowerを最大値などで規格化したデータを当たること
def power_f_time_vec(body_link, l_id, time, p_f_norm, u_vec, vec_scale=.5):
p_norm_time_vec = np.array([body_link[l_id].p[time], body_link[l_id].p[time] + \
vec_scale * np.abs(p_f_norm[time]) * u_vec[time]]).T
return p_norm_time_vec
# time を指定し power_tau()で関節に作用するトルクの力学的エネルギー変化(power)と方向:unit_vecを使用し,
# powerの線分の両端の点のlistを作る
# p_tau_normにはpower_tau()で計算したpowerを最大値などで規格化したデータを当たること
def power_tau_time_vec(body_link, l_id, time, p_tau_norm, u_vec, vec_scale=.5):
#sign = np.sign(p_tau_norm[time])
p_tau_norm_time_vec = np.array([body_link[l_id].p[time], body_link[l_id].p[time] + \
vec_scale * np.abs(p_tau_norm[time]) * u_vec[time]]).T
return p_tau_norm_time_vec次の,関数stick_power_f()とstick_power_tau()は,さらに各線分を描く関数で
# p_listでpowerの線分を描く
# p_listで線分, p_f_normで線分の太さを定める
# 色で正負を表現(正:黒, 負方向:グレー)
def stick_power_f(ax, body_link, l_id, time, p_list, p_f_norm, p_size=15,
xrange=(-1.25, .75), yrange=(0., 2.), zrange=(0., 2.),
draw_cm=False):
ax.scatter(*body_link[l_id].p[time], linewidth = 2, c='w')
lw = p_f_norm[time] * p_size # 線分の太さをpowerで定める
if draw_cm == False: # デフォルト:黒とグレーで線を描く
if np.sign(p_f_norm[time]) == 1: #powerが正の場合
lc = 'k' # 黒
else: #powerが負の場合
lc = '.5' # グレー
ax.plot(*p_list, linewidth = lw, c = lc)
# 線の色を下記のようにカラーマップから選ぶこともできる
else:
cm = plt.get_cmap('jet')
ax.plot(*p_list, linewidth = lw, c = cm(p_f_norm[time]))
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')
ax.set_xlim(*xrange)
ax.set_ylim(*yrange)
ax.set_zlim(*zrange)
ax.set_aspect('equal')
# p_listでpowerの線分を描く
# p_listで線分, p_tau_normで線分の太さを定める
# 色で正負を表現(正:赤, 負方向:水色)
# 関節から同じ部位に寄与するpowerは遠位方向のベクトルとして示す
# 関節から親の部位に寄与するpowerは親の部位の関節に向かうベクトルとして示す
def stick_power_tau(ax, body_link, l_id, time, p_list, p_tau_norm, p_size=15,
xrange=(-1.25, .75), yrange=(0., 2.), zrange=(0., 2.)):
ax.scatter(*body_link[l_id].p[time], linewidth = 2, c='w')
lw = p_tau_norm[time] * p_size # 線分の太さをpowerで定める
if np.sign(p_tau_norm[time]) == 1:
lc = 'r'
else:
lc = 'aqua'
ax.plot(*p_list, linewidth = lw, c = lc)
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')
ax.set_xlim(*xrange)
ax.set_ylim(*yrange)
ax.set_zlim(*zrange)
ax.set_aspect('equal')この関数を利用し,次のstick_power()で,引数としてlink_num_listで描く部位と,timeで時間を指定し,エネルギーの流れの線分をまとめて描く.そして,これを利用してスティックピクチャに加筆することになる.
# スティックピクチャに加筆するpowerのベクトル(線分)部分
# vec_scale: 線分の長さのスケール
# p_size: 関節の点の大きさ
def stick_power(ax, body_link, link_num_list, time, \
xrange=(-1.25, .75), yrange=(0., 2.), zrange=(0, 2.),
s_w=.000001, sf=360., lw=1, vec_scale=.5, p_size=15, max_p=3000,
draw_f_power = True, draw_tau_power = True, draw_cm=False):
# スティックピクチャ
ax.plot(*joint_p_list(body_link, time, upper_arm_list), linewidth=lw, c='C0')
ax.plot(*joint_p_list(body_link, time, body_list), linewidth=lw, c='C1')
ax.plot(*joint_p_list(body_link, time, lower_body_list), linewidth=lw, c='C2')
# make_power_data()で, powerのデータ, 線分の単位ベクトル, powerの最大値
p_f_list, p_tau_list, p_tau_parent_list, uv_child_list, uv_parent_list, max_power_data = \
make_power_data(body_link, link_num_list, s_w, sf)
if max_p == 3000:
p_norm = max_power_data
else:
p_norm = max_p
# time を指定し,関節からその先の関節を向いたパワーの大きさに応じたベクトルの線分
p_list_f = np.array([power_f_time_vec(\
body_link, link_num_list[i], time, p_f_list[i]/p_norm, uv_child_list[i], vec_scale) for i in range(len(link_num_list))])
p_list_child_tau = np.array([power_tau_time_vec(\
body_link, link_num_list[i], time, p_tau_list[i]/p_norm, uv_child_list[i], vec_scale) for i in range(len(link_num_list))])
p_list_parent_tau = np.array([power_tau_time_vec(\
body_link, link_num_list[i], time, p_tau_parent_list[i]/p_norm, uv_parent_list[i], vec_scale) for i in range(len(link_num_list))])
# パワーのベクトルを可視化
if draw_f_power == True:
[stick_power_f(ax, body_link, link_num_list[i], time, p_list_f[i], p_f_list[i]/p_norm, p_size, xrange, yrange, zrange, draw_cm)\
for i in range(len(link_num_list))]
if draw_tau_power == True:
[stick_power_tau(ax, body_link, link_num_list[i], time, p_list_child_tau[i], p_tau_list[i]/p_norm, p_size, xrange, yrange, zrange)\
for i in range(len(link_num_list))]
[stick_power_tau(ax, body_link, link_num_list[i], time, p_list_parent_tau[i], p_tau_parent_list[i]/p_norm, p_size, xrange, yrange, zrange)\
for i in range(len(link_num_list))]これを利用して,アニメーションを示す方法を次に示していく.
解析例1:飛び降りバランス動作
計算の準備
前述のエネルギーの流れの可視化で必要な親の部位の情報を,下記の関数を実行し先に定義したparent_listを利用し,インスタンス変数 parent_val に格納する.
[b_link[i[0]].set_parent(b_link[i[1]]) for i in parent_list];それ以外の解析のための準備は,これまでの力学計算と同様である.詳細はColabのコードや
などの記事を参照していただきたい.
解析
高さ20cmほどの台からの飛び降り,片足着地からのバランスを取る動作を行った際の,特に着地後の接地脚の,力とトルクによるエネルギーの流れについて解析を行う.
まず,b_link[1].ID_Newton(True),b_link[1].ID_Euler(True) によって力学計算を行う.これにより,関節に作用する力とトルクを計算する.
b_link[1].ID_Newton(86., True);
b_link[1].ID_Euler(True);得られた部位$${i}$$の力$${\bm{f}_i}$$やトルク$${\bm{\tau}_i}$$はインスタンス変数 force, tau_global に格納されている.そこで,関数 power_f(), power_tau(), power_tau_parent() により,これと格納しておいた関節の位置 p の微分で計算する関節の速度($${\bm{v}_i}$$と定める)と,事前に格納した部位$${i}$$の角速度$${\bm{\omega}_i}$$(インスタンス変数w)との内積から,力学的エネルギーの時間変化$${\bm{f}_i^T \bm{v}_i, \bm{\tau}_i^T \bm{\omega}}$$を計算する.
ここで,関節に作用する力によって発生するリンク間のエネルギーの伝達$${\bm{f}_i^T \bm{v}_i}$$をグラフで観察すると
t_list = np.arange(970,1100)/360.
plt.plot(t_list, power_f(b_link, 10)[970:1100]) # 右股関節:RThigh
plt.plot(t_list, power_f(b_link, 11)[970:1100]) # 右膝関節:RSin
plt.plot(t_list, power_f(b_link, 12)[970:1100]) # 右足関節:RFoot
plt.plot(t_list, power_f(b_link, 2)[970:1100]) # 胸部(上胴):Chest
plt.axvline(x=1005/360., c='k', ls='--')
plt.axvline(x=981/360., c='k', ls='--')
plt.ylim(-2100, 3250)
plt.xlabel('Time [s]')
plt.ylabel('Power [W]')
plt.legend(['RThigh', 'RSin', 'RFoot', 'Chest'])
のようになる(図4).最初の縦の破線は接地時間を示し,二つ目の破線は以降に示すスティックピクチャ例の時間である.下肢は地面から床反力を利用し体幹方面へエネルギーを伝達し,胸部・上胴は負の値を示していることから,体幹部でエネルギーを相殺させて吸収している様子がわかる.
一方,そのような運動を関節に作用するトルクによるエネルギーの供給・吸収$${\bm{\tau}_i^T \bm{\omega}_i}$$によってどのように実現しているかを.下記のコードと図5で確認すると,
t_list = np.arange(970,1100)/360.
plt.plot(t_list, power_tau(b_link, 10)[970:1100]) # 右股(大腿)関節トルク x 右大腿角速度:RThigh
plt.plot(t_list, power_tau_parent(b_link, 10)[970:1100]) # 右股関節トルク x 腰(下胴):RThigh2
plt.plot(t_list, power_tau(b_link, 11)[970:1100]) # 右膝(下腿)関節トルク x 右下腿角速度:RSin
plt.plot(t_list, power_tau_parent(b_link, 11)[970:1100]) # 右膝(下腿)関節トルク x 右大腿角速度:RSin2
plt.plot(t_list, power_tau(b_link, 12)[970:1100]) # 右足関節トルク x 右足角速度:RFoot
plt.plot(t_list, power_tau_parent(b_link, 12)[970:1100]) # 右足関節トルク x 右下腿角速度:RFoot2
plt.axvline(x=1005/360., c='.5', ls='--')
plt.axvline(x=981/360., c='k', ls='--')
plt.ylim(-2100, 3250)
plt.xlabel('Time [s]')
plt.ylabel('Power [W]')
plt.legend(['RThigh1', 'RThigh2', 'RSin1', 'RSin2', 'RFoot1', 'RFoot2'])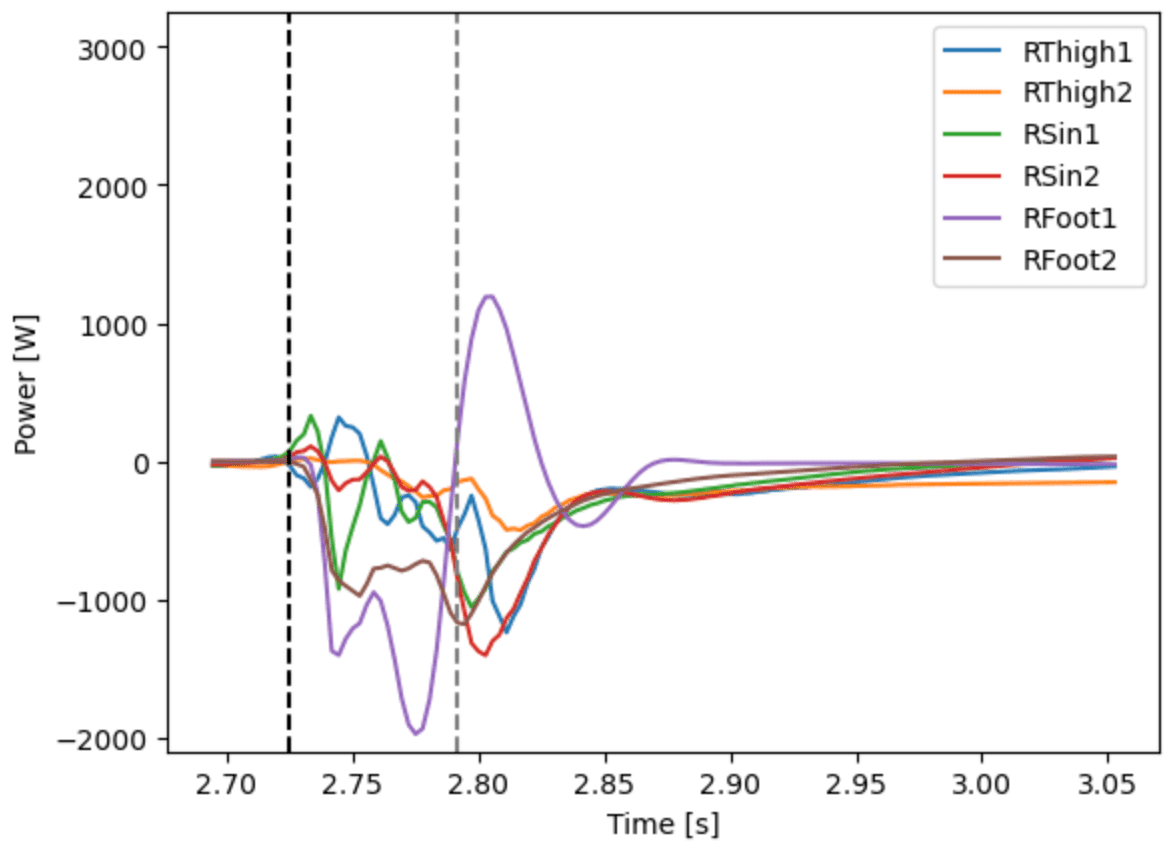
のように主として,負の値を示していることから下肢全体で,エネルギーを吸収するように努めていることがわかる.
ヒートマップによる全身のエネルギーの流れの可視化
このような様子を,上記のようなグラフの重ね書きや並べた示し方ではわかりにくい.そこで,次にヒートマップ表示による可視化でひと目で,パターンの違いを容易にする.なお,このヒートマップ表示には前述したライブラリSeabornが必要となる.
まず,関節に作用する力によって発生する部位間のエネルギーの伝達をヒートマップによって可視化する.
Seabornへのデータの受け渡しに,ライブラリPandasを使用する.Pandasの詳細は,ここでは深入りしないが,配列(numpy)で格納されるデータだけでなく,データの行や列の項目名(ここではindex, columns)も含めて,データフレームdfに格納する.
ここでは,df_f にpower_f()で計算する$${\bm{f}_i^T \bm{v}_i}$$を代入する.
df_f = pd.DataFrame(data=np.array([power_f(b_link, num) for num in range(2,16)])[:,970:1100],
index=['Chest', 'Neck', 'RUArm', 'RFArm', 'RHand', 'LUArm', 'LFArm', 'LHand', 'RThigh', 'RSin', 'RFoot', 'LThigh', 'LSin', 'LFoot'],
columns=np.round(np.arange(970,1100)/360., 3))そのデータフレームを使用し,ヒートマップ(jetというヒートマップ(色)パターンを使用)を描くと,
sns.heatmap(df_f, cmap='jet', vmin= -2000, vmax=3100)
の図が得られ,同様に,df_tau, df_tau_parent にpower_tau(), power_tau_parent()で計算する$${\bm{\tau}_i^T \bm{\omega}_i}$$を代入し,そのデータフレームを使用し,同じヒートマップで描くと,
df_tau = pd.DataFrame(data=np.array([power_tau(b_link, num) for num in range(2,16)])[:,970:1100],
index=['Chest', 'Neck', 'RUArm', 'RFArm', 'RHand', 'LUArm', 'LFArm', 'LHand', 'RThigh', 'RSin', 'RFoot', 'LThigh', 'LSin', 'LFoot'],
columns=np.round(np.arange(970,1100)/360., 3))
df_tau_parent = pd.DataFrame(data=np.array([power_tau_parent(b_link, num) for num in range(2,16)])[:,970:1100],
index=['Chest', 'Neck', 'RUArm', 'RFArm', 'RHand', 'LUArm', 'LFArm', 'LHand', 'RThigh', 'RSin', 'RFoot', 'LThigh', 'LSin', 'LFoot'],
columns=np.round(np.arange(970,1100)/360., 3))
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(15, 5))
sns.heatmap(df_tau, cmap='jet', vmin= -2000, vmax=3100, ax=ax1)
sns.heatmap(df_tau_parent, cmap='jet', vmin= -2000, vmax=3100, ax=ax2)
となる(図7).これより,主として右脚の関節に作用するトルクでエネルギーを吸収している様子がわかる.
スティックピクチャによるエネルギーの流れの可視化
先程示した,関数 stick_power() で第15章で示したスティックピクチャに,さらにエネルギー伝達$${\bm{f}_i^T \bm{v}_i}$$を書き加えるため,それを下記のコードで線分で描く.
fig = plt.figure(figsize=(10, 10))
ax = fig.add_subplot(projection='3d')
frame = 1005 # データのフレーム数(時間)
stick_power(ax, b_link, [10,11,12,2,13,14,15], frame, (-1.25, .75), (0., 2.), (0, 2.),
draw_f_power = True, draw_tau_power = False, vec_scale=.8, max_p = 3000)前述のように,線の太さと長さで,単位時間あたりの伝達量(力学的エネルギーの時間変化の量)を表し,色(黒・正:親から子供の方向,グレー・負:子から親の方向)で伝達の方向を示す.
なお,ここで関数のオプション(引数)としてdraw_tau_power = Falseとすることで,トルクが生成する流れ$${\bm{\tau}_i^T \bm{\omega}_i}$$は表示させていない.

同じ$${\bm{f}_i^T \bm{v}_i}$$を,draw_cm = Trueとすることで,ヒートマップと同様にスティックピクチャ上にさらに色の変化を付けて可視化すると,
fig = plt.figure(figsize=(10, 10))
ax = fig.add_subplot(projection='3d')
frame = 1005 # データのフレーム数(時間)
stick_power(ax, b_link, [10,11,12,2,13,14,15], frame, (-1.25, .75), (0., 2.), (0, 2.),
draw_f_power = True, draw_tau_power = False, vec_scale=.8, max_p = 3000,
draw_cm = True)
のように描くことができる(図9).
同様に下記のコードで,トルクが行うエネルギーの供給・吸収$${\bm{\tau}_i^T \bm{\omega}_i}$$をスティックピクチャ上に可視化する.
fig = plt.figure(figsize=(10, 10))
ax = fig.add_subplot(projection='3d')
frame = 1005 # データのフレーム数(時間)
stick_power(ax, b_link, [10,11,12,2,13,14,15], frame, (-1.25, .75), (0., 2.), (0, 2.),
draw_tau_power = True, draw_f_power = False, vec_scale=.8, max_p = 3000)
同様に線の太さと長さで,単位時間あたりの移動量(力学的エネルギーの時間変化の量)を表し,色(赤・正:供給,青・負:吸収)で伝達の方向を示す.
また,ここで関数のオプション(引数)としてdraw_f = Falseとすることで,力が生成する流れ$${\bm{f}_i^T \bm{v}_i}$$を表示していない.
可視化のオプションを両方Trueにし,
fig = plt.figure(figsize=(10, 10))
ax = fig.add_subplot(projection='3d')
frame = 1005 # データのフレーム数(時間)
stick_power(ax, b_link, [10,11,12,2,13,14,15], frame, (-1.25, .75), (0., 2.), (0, 2.),
draw_tau_power = True, draw_f_power = True, vec_scale=.8, max_p = 3000)
図11のようにすることもできる.
第15章で示したように,これをスライダーバーで下記のコードで動かすと
def stick_power_plot_jump(body_link,
xrange=(-1.25, .75), yrange=(0., 2.), zrange=(0, 1.5),
s_w=.000001, sf=360., lw=1, vec_scale=.5, p_size=15, max_p=3000,
draw_tau_power = True, draw_f_power = True):
step_frame = 10 # アニメーションの際の描画でスキップするフレーム数
q = len(body_link[10].p) // step_frame # フレーム数をstep_sizeで割った,整数の商
max_frame = q * step_frame # 描画する最大フレーム数
step_time = .01
sf = 360.
q = (len(body_link[10].p) / sf) // step_time # フレーム数をstep_sizeで割った,整数の商
max_time = q * step_time
@interact(time = FloatSlider(min=0, max=max_time, step=step_time, value=0, continuous_update=True), # 描画する時間 [s]
elev = IntSlider(min=-10, max=90, step=5, value=0, continuous_update=True), # ViewPoint(視点)の仰角
azim = IntSlider(min=-100, max=180, step=5, value=-100, continuous_update=True)) # ViewPointの方位角
def plot_3d(elev, azim, time):
fig = plt.figure(figsize=(10, 10))
ax = fig.add_subplot(projection='3d')
ax.view_init(elev=elev, azim=azim)
time2 = int(time * sf)
stick_power(ax, b_link, [10,11,12,2,13,14,15], time2, xrange, yrange, zrange,
s_w, sf, lw, vec_scale, p_size, max_p,
draw_f_power, draw_tau_power)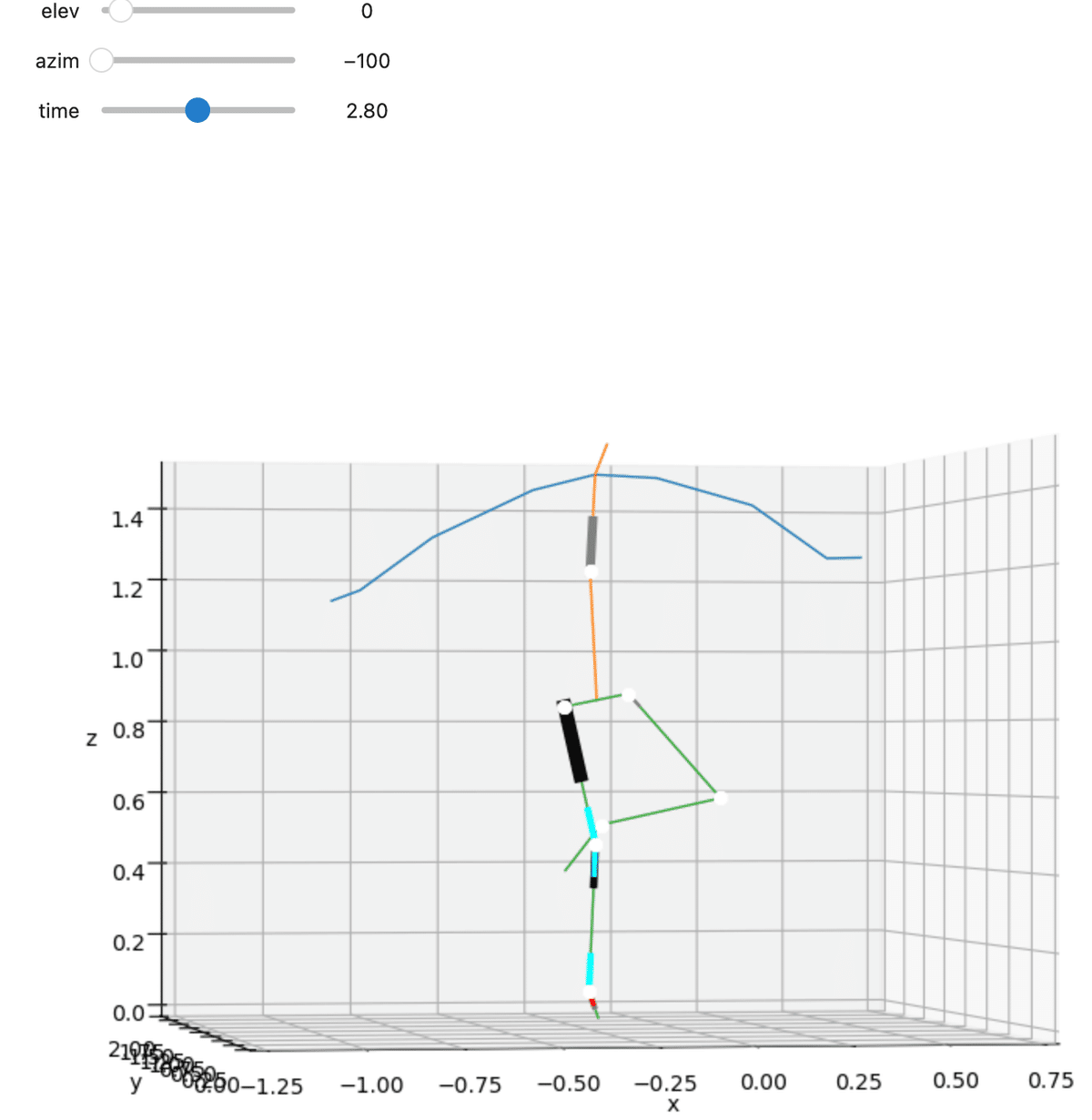
のように動かすことができる.
解析例2:投球動作
クラスの定義,関数は解析例1と共通である.計算の「準備」については割愛するが,下記のように暮らすBodyLinkで定義された配列b_link2にデータを格納する.その他の,コードの詳細はColabに示すが,解析例1とほぼ同様である.
b_link2 = [0] * 27 # 配列の初期化
b_link2[0] = BodyLink(0, '', '', .0, .0) # 0のときストップ
b_link2[1] = BodyLink(1, 'Hip', 'Bone', .187, (1.-.609)) # 腰(下体幹)
b_link2[2] = BodyLink(2, 'Chest', 'Bone', .302, (1.-.428)) # 胸(上体幹)
b_link2[3] = BodyLink(3, 'Neck', 'Bone', .069, (1.-.821)) # 頭部
b_link2[4] = BodyLink(4, 'RUArm', 'Bone', .027, .529) # 右上腕
b_link2[5] = BodyLink(5, 'RFArm', 'Bone', .016, .415) # 右前腕
b_link2[6] = BodyLink(6, 'RHand', 'Bone', .006, .891) # 右手
b_link2[7] = BodyLink(7, 'LUArm', 'Bone', .027, .529) # 左上腕
#b_link2[8] = BodyLink(8, 'LFArm', 'Bone', .016, .415) # 左前腕
b_link2[8] = BodyLink(8, 'LELB', 'Bone Marker', .016, .415) # 左前腕
b_link2[9] = BodyLink(9, 'LHand', 'Bone', .006, .891) # 左手
b_link2[10] = BodyLink(10, 'RThigh', 'Bone', .110, .475) # 右大腿
b_link2[11] = BodyLink(11, 'RShin', 'Bone', .051, .406) # 右下腿
b_link2[12] = BodyLink(12, 'RFoot', 'Bone', .011, (1.-.595)) # 右足
b_link2[13] = BodyLink(13, 'LThigh', 'Bone', .110, .475) # 左大腿
b_link2[14] = BodyLink(14, 'LShin', 'Bone', .051, .406) # 左下腿
b_link2[15] = BodyLink(15, 'LFoot', 'Bone', .011, (1.-.595)) # 左足
# 各リンクの遠位端も定義(遠位端の位置ベクトルを計算するためだけに必要な変数
b_link2[16] = BodyLink(16, 'Head', 'Bone', .0, .0) # 3 Neckの遠位端
b_link2[17] = BodyLink(17, 'RFIN', 'Bone Marker',.0, .0) # 6 RHandの遠位端
b_link2[18] = BodyLink(18, 'LFIN', 'Bone Marker', .0, .0) # 9 LHandの遠位端
b_link2[19] = BodyLink(19, 'RToe', 'Bone', .0, .0) # 12 RFootの遠位端
b_link2[20] = BodyLink(20, 'LToe', 'Bone', .0, .0) # 15 LFootの遠位端
# 手,前腕の姿勢回転行列を計算するためだけに必要な変数
b_link2[21] = BodyLink(21, 'RWRA', 'Bone Marker', .0, .0) # 右手首橈骨側
b_link2[22] = BodyLink(22, 'RWRB', 'Bone Marker', .0, .0) # 右手首尺骨側
b_link2[23] = BodyLink(23, 'LWRA', 'Bone Marker', .0, .0) # 左手首橈骨側
b_link2[24] = BodyLink(24, 'LWRB', 'Bone Marker', .0, .0) # 左手首尺骨側
b_link2[25] = BodyLink(25, 'RFHD', 'Bone Marker', .0, .0) # 右前頭
b_link2[26] = BodyLink(26, 'LFHD', 'Bone Marker', .0, .0) # 左前頭解析
解析方針:
投球時の,右腕(利き腕)の,力とトルクによるエネルギーの流れについて解析を行う.ただし,残念ながらフォースプレートの床反力データがないために,下肢の力学解析が行えない.
しかし,特に投球時の下肢・体幹のエネルギーは,恐らくボールの加速のエネルギー源となっている.そこで,これまでにも示してきたように,総和の床反力は推定できるので,機会があれば左右脚への分配の推定方法を考え,下肢の力,トルク,エネルギーの流れを可視化することを試みたい.
注意:
下記の解析では,ボールの扱いが変則的かつ中途半端で,
1.ボールの計測も行っているが,このモデルにボールを与えておらず,手にボールの質量0.147 kgを下記のコードで加算した.
2.Google Colabのコードでは「#でコメントアウトしている」!
3.以下に示す計算結果では.ボールの質量を手に加算した結果を「反映している」!.
4.慣性モーメントに変更を与えていない.
として,クラスBodyLinkのメソッドCgForce()にボールの質量を次のコードのように考量した.
# m * (acc - g)
def CgForce(self, bw):
gravity = [0., 0., -9.8] # 重力加速度ベクトル
if self.l_id == 6:
return (bw * self.mass_ratio + .147) * (self.acc - gravity)
else:
return bw * self.mass_ratio * (self.acc - gravity)いずれボールを含めたモデルによる解析も示したい.
解析:
まず,b_link[1].ID_Newton(True),b_link[1].ID_Euler(True) によって力学計算を行う.これにより,関節に作用する力とトルクを計算する.
b_link[1].ID_Newton(86., True);
b_link[1].ID_Euler(True);次に,関節に作用する力によって発生するリンク間のエネルギーの伝達$${\bm{f}_i^T \bm{v}_i}$$を,右腕に関してグラフで観察すると,
e_t = 257
t_list2 = np.arange(0, e_t)/360.
plt.plot(t_list2, power_f(b_link2, 4)[:e_t])
plt.plot(t_list2, power_f(b_link2, 5)[:e_t])
plt.plot(t_list2, power_f(b_link2, 6)[:e_t])
plt.ylim(-2100, 7000)
plt.axvline(x=256/360., c='.5', ls='--') # ball release
plt.xlabel('Time [s]')
plt.ylabel('Power [W]')
plt.legend(['RUArm', 'RFArm', 'RHand'])
のようになる(図13).破線はボールリリース時間を示す.肩を介して右上腕から右手(ボール)へとエネルギーが伝達している様子がわかる.
これに対して,関節に作用するトルクによるエネルギーの供給・吸収$${\bm{\tau}_i^T \bm{\omega}_i}$$によって投球運動をどのように実現しているかを.下記のコードと図14, 15で確認すると,
e_t = 257
t_list2 = np.arange(0, e_t)/360.
plt.plot(t_list2, power_tau(b_link2, 4)[:e_t])
plt.plot(t_list2, power_tau(b_link2, 5)[:e_t])
plt.plot(t_list2, power_tau(b_link2, 6)[:e_t])
plt.ylim(-2100, 7000)
plt.axvline(x=256/360., c='.5', ls='--') # ball release
plt.xlabel('Time [s]')
plt.ylabel('Power [W]')
plt.legend(['RUArm1', 'RFArm1', 'RHand1'])
e_t = 257
t_list2 = np.arange(0, e_t)/360.
plt.plot(t_list2, power_tau_parent(b_link2, 4)[:e_t], ls='--')
plt.plot(t_list2, power_tau_parent(b_link2, 5)[:e_t], ls='--')
plt.plot(t_list2, power_tau_parent(b_link2, 6)[:e_t], ls='--')
plt.ylim(-2100, 7000)
plt.axvline(x=256/360., c='.5', ls='--') # ball release
plt.xlabel('Time [s]')
plt.ylabel('Power [W]')
plt.legend(['RUArm2', 'RFArm2', 'RHand2'])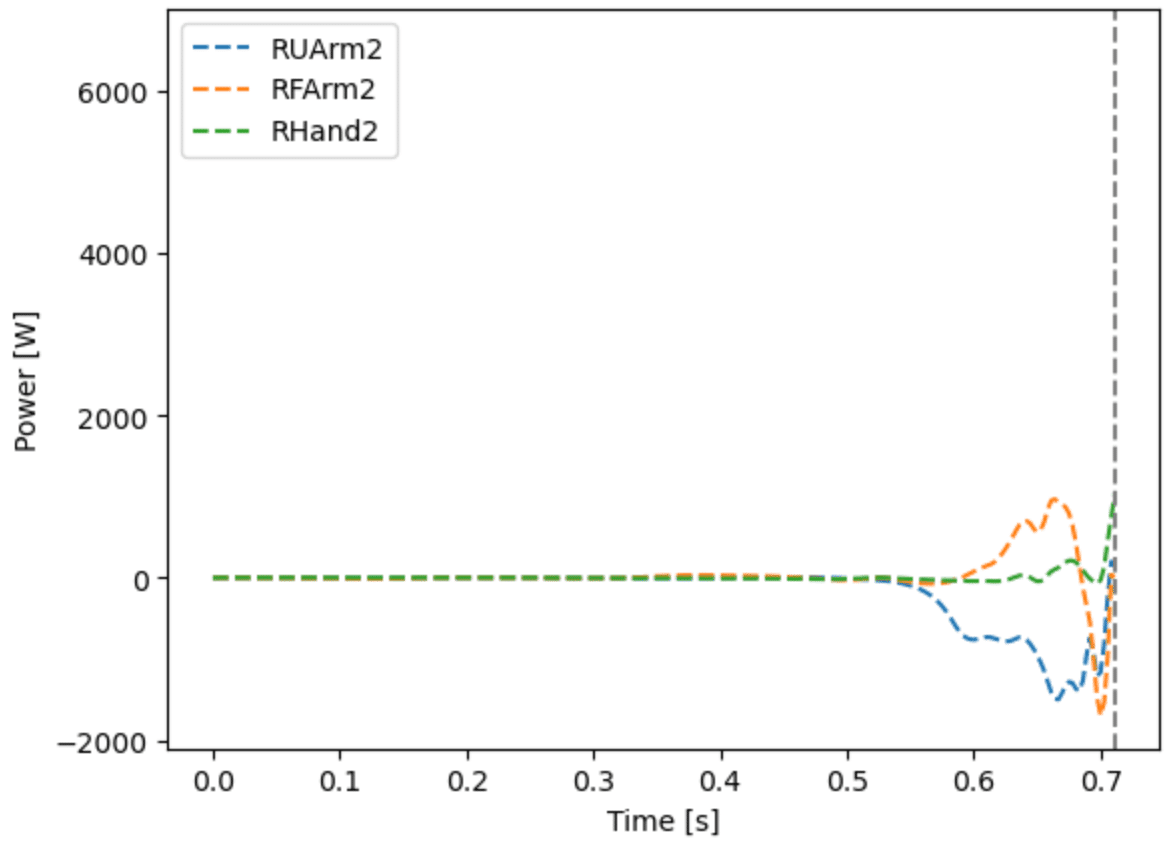
のように主として,肩まわりのトルクがエネルギー供給元であることがわかる.
スライダーバーによるエネルギーの流れの可視化:
解析例1と同様に,スライダーバーで手動で動かしたり(図16)
stick_power_plot_throw(b_link2,
xrange=(-.5, 2.), yrange=(-1., 1.6), zrange=(0, 2),
s_w=.0001, sf=360., lw=1, vec_scale=.5, p_size=15, max_p=5000.,
draw_tau_power = True, draw_f_power = True, time_end = 0.712)
下記のような方法で,アニメーションの実行や動画を作成することができる.
# アニメーションで使用する重心と,床反力(重心の加速度から計算)
cg = b_link2[1].Resultant_Cg(86., True) # 重心位置
cg_acc = smoothing_spline(b_link2[1].Resultant_Cg(86., True), .00005, 360., 2)-[0., 0., -9.8] # 重心位置の加速度+重力加速度
t_list = np.arange(len(b_link2[1].p))/360.x_range = (-.2, 1.75) # x軸描画範囲
y_range = (-.5, 1.) # y軸描画範囲
z_range = (0., 2.1) # z軸描画範囲
p_elev = 20
p_azim = -110
f_len = 260 # len(b_link2[10].p) # 今回は終わりのフレームを指定した
step_frame = 5 # アニメーションの際の描画でスキップするフレーム数
q = f_len // step_frame # フレーム数をstep_sizeで割った,整数の商
max_frame = q * step_frame # 描画する最大フレーム数
sf = 360. # サンプリングレート
m = 86. #体重
# 3Dグラフ領域の作成
fig = plt.figure(figsize=(10, 10))
ax = fig.add_subplot(projection='3d')
ax.view_init(elev=p_elev, azim=p_azim)
# アニメーション更新用関数の作成
def plot_3d(frame):
ax.cla()
# 細い線でスティックピクチャを重ね描画
[stick(ax, b_link2, time, .1, x_range, y_range, z_range) for time in range(0, max_frame, 10)]
frame_new = step_frame * frame
stick_power(ax, b_link2, [4, 5, 6], frame_new, \
x_range, y_range, z_range,
lw=2, vec_scale=.5, p_size=15, max_p=5000,
draw_f_power = True, draw_tau_power = True)
# 重心に作用する力(=床反力の合力)のベクトル
ax.scatter(*cg[frame_new], s=50, c='k') # 重心
scale = .05
ax.plot([cg[frame_new, 0], cg[frame_new, 0] + scale * cg_acc[frame_new, 0]],
[cg[frame_new, 1], cg[frame_new, 1] + scale * cg_acc[frame_new, 1]],
[cg[frame_new, 2], cg[frame_new, 2] + scale * cg_acc[frame_new, 2]], c='r', linewidth=2)
# アニメーションのオブジェクトを作成
anim = FuncAnimation(fig, plot_3d, frames = q, interval = 50)
# Jupyter内でアニメーションの表示
plt.close()
HTML(anim.to_jshtml())
### Gif/MP4に保存する場合 ###
# path_dir = '/Users/.../sample_data/'
# path = pathlib.Path(path_dir)
# path_gif = path.joinpath('animation_power.gif')
# path_mp4 = path.joinpath('animation_power.mp4')
# anim.save(path_gif)
# plt.close()




【著作権・転載・免責について】
権利の帰属
本ホームページで提示しているソフトウェアならびにプログラムリストは,スポーツセンシング社の著作物であり,スポーツセンシング社に知的所有権がありますが,自由にご利用いただいて構いません.
本ページに掲載されている記事,ソフトウェア,プログラムなどに関する著作権および工業所有権については,株式会社スポーツセンシングに帰属するものです.非営利目的で行う研究用途に限り,無償での使用を許可します.
転載
本ページの内容の転載については非営利目的に限り,本ページの引用であることを明記したうえで,自由に行えるものとします.
免責
本ページで掲載されている内容は,特定の条件下についての内容である場合があります. ソフトウェアやプログラム等,本ページの内容を参照して研究などを行う場合には,その点を十分に踏まえた上で,自己責任でご利用ください.また,本ページの掲載内容によって生じた一切の損害については,株式会社スポーツセンシングおよび著者はその責を負わないものとします.
【プログラムの内容について】
プログラムや内容に対する質問に対しては,回答できないことのほうが多くなると思いますが,コメントには目は通します.回答は必要最低限にとどめますので,返信はあまり期待しないでいただけると幸いです,
「動かして学ぶ」という大それたタイトルをつけたものの,また,きれいなプログラムに対するこだわりはあるものの,実際のプログラミングのスキルは決して高くありません.最下部の方のコメント欄によるプログラムの間違いのご指摘は歓迎します.できるだけ反映します.
【解析・受託開発について】
スポーツセンシングでは,豊富な知見を持つ,研究者や各種エンジニアが研究・開発のお手伝いをしております.研究・開発でお困りの方は,ぜひスポーツセンシングにご相談ください.
【例】
・データ解析の代行
・受託開発
(ハードウェア、組込みソフトウェア、PC/モバイルアプリ)
・測定システム構築に関するコンサルティング など
その他,幅広い分野をカバーしておりますので,まずはお気軽にお問い合わせください.
【データの計測について】
スポーツセンシング社のスタジオで,フォースプレートやモーションキャプチャを利用した計測も行えます.出力されるデータと,ここで示したプログラム(入力データの取り込み関数を少々改変する必要があるが)で,同様な解析を行えますので,まずはお気軽にお問い合わせください.
