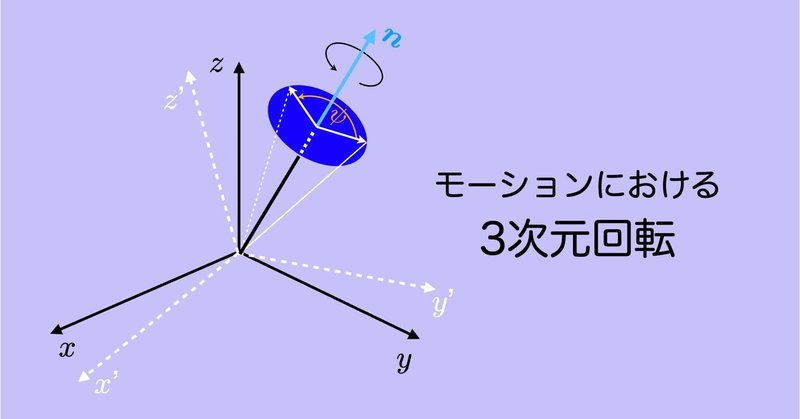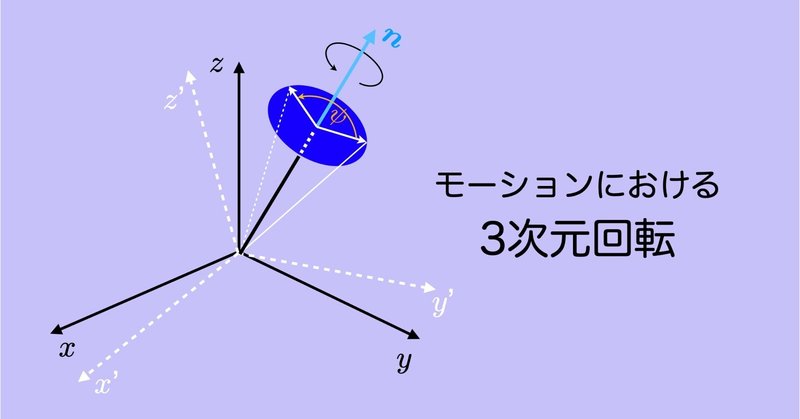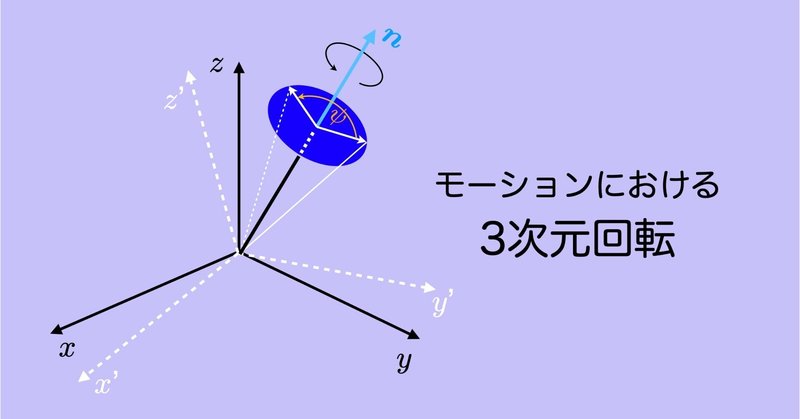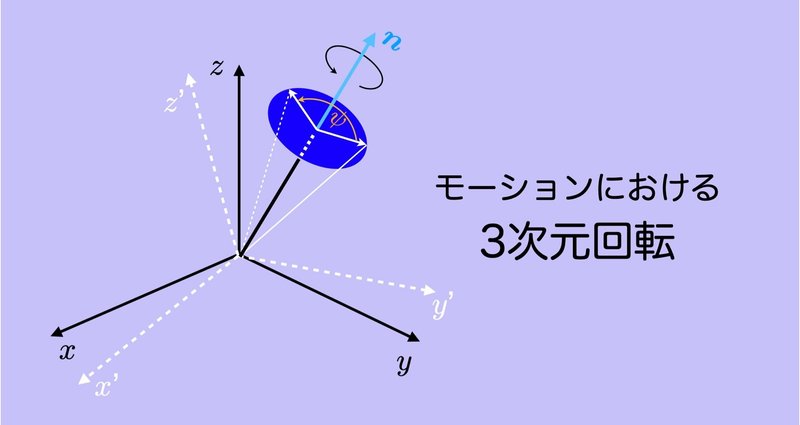
運動計測では,3次元回転に関する数学的理解が不可欠です.しかし,バイオメカニクスの教科書には詳しい解説は見当たりません.単位クォータニオンを中心に他の分野でも書かれていないことも…
- 運営しているクリエイター
#クォータニオン積
モーションにおける3次元回転 #9 〜3次元回転・公式集〜
最近では,モーションセンサやモーションキャプチャの出力も単位クォータニオンの出力が標準になりつつあり,3次元回転を扱うには単位クォータニオンの理解が不可欠である.
そこで,ここまで述べてきた3次元回転の式を単位クォータニオンによる表現を中心に以下にまとめる.
3次元回転を理解する上でオイラー角の理解も必要ではあるが,実際の計算では,ここで述べてきた単位クォータニオンのベクトルや行列表現に慣れる
モーションにおける3次元回転 #8 〜単位クォータニオンによる回転合成〜
単位クォータニオンの演算ここでは,回転合成と前章まで議論したロドリゲスの式の,単位クォータニオン(オイラーパラメータ)による表現を示す.
回転合成の節では,行列表現によってクォータニオン同士の線形計算ができることを示すが,この行列表現を用いることでMatlab, Python(Numpy)などの行列計算を利用でき,プログラミングの記述も行いやすくなり.計測制御の観点では,行列表現によってKalm
モーションにおける3次元回転 #6 〜クォータニオンの導入〜
単位クォータニオンとオイラーパラメータクォータニオン(quaternion)は四元数(しげんすう)とも呼ばれ,アイルランドの数学者ハミルトンが1843年に,現在ウィリアム・ローアン・ハミルトン橋と呼ばれている橋を歩いているときに,ひらめき,そのアイデア(下記の式)を橋にナイフで刻んだと伝えられている.
なお,回転を含めた2次元平面の幾何学を記述する複素数が,4次元へ拡張されたのものがクォータニオ