
【スマホでPython数学】 第5章 2つの関数と連立方程式の解
第4章にてグラフの描き方が分かったと思います。毎回違う座標軸にグラフを描いてきましたが、一つの座標軸に2つのグラフを描いてみたい、と思いませんでしたか?前回はx軸との交点が方程式の解でしたが、今回は2つのグラフの交点が連立方程式の解になるというお話になります。
1.plot(プロット)命令で2つのグラフを同時に描画
基本は第4章と同じで、Sympyモジュールのplot(プロット)命令を使います。型は一緒ですが、2つの関数を(カッコ)の中に「,(カンマ)」で区切って記載するだけです。xの値の範囲についても同じように指定できます。
それでは、以下の例題をやってみましょう。
例題1:$${y=x^3-2x^2 -2x +3}$$と$${y=-x+1}$$の2つの関数のグラフを描いてみましょう。
from sympy import *
var('x')
plot(x**3-2*x**2 -2*x +3, -x+1, (x, -2, 3))
実はこの三次関数と直線の2つグラフの交点は、$${x=-1, 1, 2}$$となっています。これは、$${x^3-2x^2 -2x +3=0}$$と$${-x+1=0}$$の連立方程式の解でもあります。整数の解が3つあったと言うことになります。
それでは、Pythonを使った連立方程式の解き方の型を覚えましょう。
2.関数を定義する
すでに関数は扱ってきたのですが、その定義は曖昧にしていました。今後は次のような型で関数を定義する事にしましょう。(本書で便宜的に決めただけですので、慣れてきたらご自由に決めていただいて結構です。)
高校の数学ですと、$${f(x)=x^3-2x^2+x-5}$$という表記になりますが、ここでは適当なアルファベットと数字を使ってみます。
f1 = x**3 -2*x**2 -2*x +3
f2 = -x +1上記のように2つの関数を定義しました。すると、plot関数の記述がややすっきりしてきます。
plot(f1, f2, (x, -2, 3))plot関数の(カッコ)の左にf1、f2という関数があり、右に「(x, -2, 3)」とxの範囲が定義されています。
3.連立方程式の解法
方程式の解法については、第6章で詳しくやりますので、ここでは連立方程式の解き方だけご紹介します。
$${3x^3−2x^2−2x+3 = 0}$$
$${-x+1 = 0}$$
先ほどの2つの関数(f1, f2)でしたら、2つの関数を引き算するだけです。
F = f1 - f2
solve(F)いかがでしたか?答えが出ましたか?
解は[-1, 1, 2]です。($${x = -1, 1, 2}$$)
今回はSympyモジュールのsolve(ソルブ)関数を使っています。関数Fを因数分解しても面白い結果になると思います。力が余っている方はやってみてください。
ちなみに関数Fのグラフを$${-2<x<3}$$の範囲で書いてみてください。$${x}$$軸との交点が連立方程式の解でもあります。
plot(F,(x,-2,3))
それではいくつか演習問題を置いておきます。
まず、関数を定義します。その後に2つの関数のグラフを描いて、交点を探してください。その後に連立方程式を解いてみてください。
演習1:以下の2つの方程式の解を求めてください。
$${−3x^3−5x^2+10x+8 = 0}$$
$${x^2−5x−10 = 0}$$
演習2:
$${x^3−3x^2+4x+1 = 0}$$
$${2x^2-2x+1 = 0}$$
まとめ
第5章は微積分などでもう少し深く学習できる機会がありますので、ここでは関数の定義とplot関数の使い方を覚えていただければ十分です。
解答
演習1:
f3 = -3*x**3-5*x**2+10*x+8
f4 = x**2-5*x-10plot(f3,f4, (x,-4,3))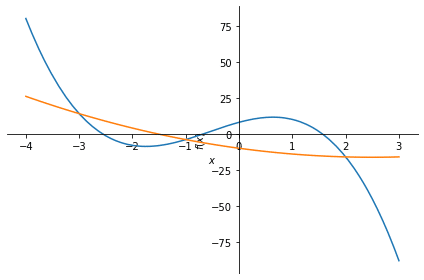
F = f3 - f4
solve(F)解は[-3, -1, 2]になります。($${x = -3, -1, 2}$$)
演習2:
f5 = x**3-3*x**2+4*x+1
f6 = 2*x**2-2*x+1F = f5 -f6
solve(F)解は[0, 2, 3]($${x = 0, 2, 3}$$)
ついでにFのグラフを書くと、$${x}$$軸との交点が解になります。
plot(F, (x, -1,4))
この記事が気に入ったらサポートをしてみませんか?
