
私の幻の博士論文 第6回 IAA―関節トルクの関節力への貢献の定量―
前回
1. はじめに
前回は、垂直跳びのパフォーマンス(跳躍高)に対して、動作開始から離地までの間の時々刻々において身体各所に作用する上下方向の並進力(関節力と重力)がどの程度貢献しているのかを定量的に比較・評価する際の考え方について紹介しました。他方で、前回紹介した内容だけだと、ある種の不満点が残ってしまうということも、最後に少しお話ししました。
まずは、「残ってしまう不満点」とは一体何なのかということについて確認していきたいと思います。それは、「関節力や重力のパフォーマンスに対する貢献が分かるだけでは、その知識を生かして選手や指導者が何を目指せば良いのかがはっきりしない」ということです。
この説明だけだとよく分からないと思うので、何が問題となるのかについて、もう少し具体的にお話しする必要があると思います。そこで、関節トルクと関節力の違いという観点から、この点についてもう少し詳しく考察してみたいと思います。
第4回において、関節トルクとは、「ある関節をまたいで付着している複数の筋が発揮した力によって生じる、トルク(セグメントを回転させる作用)を合算したもの」だということをお話ししました。したがって、第4回において紹介した「逆動力学的アプローチによって関節トルクを推定」する手法のみでは、ある動作中に「1つ1つの筋が個別に」どれくらいの大きさの力を発揮しているのかをはっきりと特定することはできません。
それでも、例えば大きな膝関節トルクが発揮されているという場合には、膝関節をまたぐ大腿四頭筋、ハムストリングス、腓腹筋などのうち、少なくともいずれかの筋が大きな力を発揮しているのだということは分かります。したがって、膝関節トルクがパフォーマンスに対して大きな貢献をしているという知見からは、膝関節をまたぐ筋群のいずれかをもっと鍛えたり、より活発に動員したりすることがパフォーマンスを向上させることにつながるのではないかといった教訓を導くことができそうです。
※前回の冒頭でも示唆しましたが、このような推論をすることには問題があると私は考えていますが、この点については、別の回にて考察します。
これに対して、ある瞬間にある関節に作用している関節力がパフォーマンスに大きな貢献をしているという知見が得られたとしても、そこから何に取り組めば良いのかという教訓を引き出すのは困難です。それは何故かというと、ある関節トルクの発生原因となるのが、その関節をまたいで付着している筋による力発揮のみであったのに対して、ある関節力の発生に対しては、より多くの要素が原因となり得るからです。
具体的には、まず、ある関節に作用する関節力の発生に対しては、その関節以外の関節トルクが関与し得ます。また、重力や角速度が存在している(ゼロではない)ことも、関節力の発生原因となり得ます。
そして、厄介なことに、逆動力学的アプローチによって関節トルクを推定する手法のみによっては、これら全身に作用・発生している関節トルク、重力、角速度の存在が原因となって、身体各関節においてどのような関節力が発生するのかは分かりません。
※それに対して、前回紹介した内容までであれば、逆動力学的アプローチによって関節トルクを推定する手法の他に必要になるのは、比較的簡単な追加的計算のみです。
この問題を解決してくれる解析手法としてInduced Acceleration Analysis (IAA) というものがあります。IAAは、全身の各セグメントに作用・発生している個別の関節トルク、重力、角速度が原因となって、全身の各セグメントに対してどのような関節力・加速度・角加速度が発生したかを定量するための手法です。IAAは、1990年代後半あたりから、バイオメカニクス的動作解析の研究分野内で大きな注目を集めるようになり、現在ではかなり多くの研究論文において、この手法が用いられています。
IAAとはどのような研究手法かということについては、
$${\ddot{\theta} = I^{-1} (T + G + V)}$$
という数式が、IAAの一般式として示され、$${I^{-1} T}$$ は関節トルクの、 $${I^{-1} G}$$ は重力の、 $${I^{-1} V}$$ は角速度の身体各セグメントに発生する角加速度への貢献を表現した項であるといった説明がされることがあります。しかし、この説明だけだと何が何やら分からないという方も多いと思います(私もこのような説明を最初に目にした時は非常に困惑しました)。そこで今回は、IAAという解析手法が、具体的にはどのような作業を行うものなのかという点について、もう少し詳しく紹介してみたいと思います。
今回は計算式がたくさん出てきてしまいますが、細かな計算手続きを覚えたり、正確に理解したりする必要は、私の今回の連載を理解する上では必要ありません。しかし、今後の回で私が行う議論を楽しんでもらうためには、IAAが原理的にはどのような解析手法なのかという点についての大まかな理解は持っていただいた方が良いと思います。そこで、まずはまったく得体の知れないものという状況を脱して、だいたいこういう感じの作業が行われているのだなということを把握するという程度の軽い気持ちでお読みいただいて、後の回でIAAに言及された際に、適宜今回の内容を振り返るというような読み方をしていただければ幸いです。
2. 関節力が発生する原理についての直観的イメージ
前節では、全身に作用・発生する関節トルク、重力、角速度が関節力の発生原因になり得るということをお話ししました。この点について、「本当にそうなるのか」であるとか、あるいは、「どうしてそうなるのか」といった疑問を持たれた方もいるのではないかと思います。
次節以降では、具体的な計算式の立て方について紹介していきますが、その前に本節では、上のような疑問が生じ得ることを念頭において、こうした因果関係が存在することについて、ある程度の納得感が得られるのではないかと私が考えている視覚的イメージ(と簡単な論理的思考)を提示してみたいと思います。
まずは、関節トルクが発揮されることによって関節力が発生する原理について考えてみたいと思います。図1は、セグメントの左端において関節トルクが作用したことによって、重心を中心にセグメントを回転させるような角加速度が発生した状況を表しています。

セグメントに角加速度が発生する
セグメントが重心を中心に回転している場合、図2のように、セグメント重心の位置は変化しませんが、セグメント末端の位置には変化(並進加速度)が生じます。

よって末端は並進する
そして、図3のように、右端に別のセグメントが連結されていたとしたら、この連結が常に維持されるという条件の下では、この第2のセグメントの左端の位置も一緒に移動することになります。この時、第1のセグメントによって第2のセグメントに対して押したり引っ張ったりする力が作用することは直観的にイメージしやすいと思います。これが、関節トルクが作用することによって関節力が発生する基本的な原理です。

いると関節力が発生する
さらに、図4のように、第2のセグメントの反対端に第3のセグメントがさらに連結されている場合には、第1のセグメントの左端で作用した関節トルクは、第3のセグメントの挙動にまで影響を及ぼします。そして、その先に第4、第5・・・のセグメントが連結している場合には、同様の原理で影響が及ぶことになります。
※図4を見ると、①~⑤の出来事が時系列順に生じるような印象を持たれるかもしれませんが、実際には、これらはすべて同時に生じます。

離れたセグメントにまで及ぶ
このように、関節トルクには、それが直接的に作用するセグメント以外にも関節力(とそれによって発生する並進加速度、トルク、角加速度)を発生させるという性質があります。このことは、関節トルクが有している遠隔的効果(Remote effect)として良く言及されています。
関節トルクが原因となって発生する関節力としては、この遠隔的効果が注目されがちです。しかし、関節トルクが、それが発揮された関節自体の関節力発生の原因にもなるということは、あまり表立って言及されることはありません。それもあってか、私が関節トルクの遠隔的効果についての解説を最初に読んだ時には、「関節トルクは、発揮された関節自体の関節力には影響を及ぼさない」という誤った理解をしてしまっていました。
そこで、関節トルクは、その関節自体の関節力発生の原因にもなり得るのだということを直観的に納得できるような視覚的イメージについても提示しておきたいと思います。なお、この点については、本質的内容としては、第4回において既に別の文脈で説明していることの繰り返しになりますが、今回はその時とは別の状況設定を用いて説明をしてみますので、そちらも合わせて確認してみると理解が促進されるかもしれません。
図5は、地面に静止した(=速度、角速度がゼロの)状態で寝かせられた2つのセグメントが互いに連結しており、連結ポイントをまたいで付着している筋が発揮した力によって関節トルクが発生している状況を表しています。2つのセグメントを地面に寝かせられた設定にしているのは、重力がセグメントの挙動に影響を及ぼさない状況について考えた方が分かりやすいからです。

関節トルクが作用している状況
第4回において紹介したように、関節トルクによって生じる第1次的な効果は、それぞれのセグメント重心を中心とした回転を加速させるような角加速度を発生させることです。したがって、仮に2つのセグメントが連結して離れないという条件が存在しない場合は、図6のように、2つのセグメントはそれぞれの重心を中心として回転し、結果的にセグメント同士は離れ離れになってしまいます。

いない場合に生じる挙動
それに対して、セグメント同士の連結が保たれ続けるという条件下では、関節トルクが作用することで生じる2つのセグメントの挙動は、図7のようなものになると考えられます。

いる場合に生じる挙動
図7を見てみると、2つのセグメントは共に重心位置が変化していることが分かります。重心位置が変化したということは、言い換えるとセグメント重心に並進速度が発生した(ゼロではなかった)ということです。そして、元々は静止状態であることを仮定していたので、速度なし(ゼロ)から速度あり(ゼロではない)への加速(並進加速度)が生じていたということになります。さらに、重心に並進加速度が生じているということは、セグメントに作用している並進力(の合計値)がゼロではないということを意味します。
第4回において、セグメントの並進運動を表現するための運動方程式を立てた際に、セグメントに並進力を作用させる要素として式に含まれていたのは、重力と関節力です。先ほど述べたように、セグメントが地面に寝かせられた状況について考えていることから、重力は両セグメントの動きには影響しません。したがって、両セグメント重心の並進加速度が変化するためには、(他の力の発生源の候補が存在しない以上)関節力が生じていなければならないと結論づけることができます。このように考えてみることで、関節トルクが作用することによって、その関節自体の関節力も発生するということが直観的に理解できます。
次に、重力が存在することによって関節力が発生する原理についても考えてみましょう。図8は、左端が地面の一点から動かないように拘束された1つのセグメントの右端が上から吊るされることで静止している状況を表しています。この状況から、上からの支えがなくなったとしたら、セグメントにどのような挙動が生じるのかを考えてみましょう。

右端が上から支えられている状況
静止した状態を想定しているので、セグメントの角速度はゼロです。また、関節トルクも作用していないものとしましょう。つまり、関節力の発生原因となり得るとお話しした関節トルク、重力、角速度のうち、重力のみが存在しているという状況にあるということです。
仮に地面が存在していなかったら(したがって、地面とセグメント左端との拘束も存在していなかったら)、図9のように、セグメントは姿勢角を保ったまま落下していくことになります。

存在しない場合に生じる挙動
しかし、地面が存在し、その地面にセグメント左端が拘束されているという条件の下では、図10のように、セグメントは単純に落下していくのではなく、左端を中心として弧を描くように落下していく挙動になるはずです。

存在する場合に生じる挙動
この場合も、セグメントの重心位置は変化しています。止まった状態について考えているため、関節トルクについて考えた時と同様のロジックで、セグメントに対して並進力が作用している(並進力の合計値がゼロではない)ことが分かります。
もっとも、先ほどのケースとは異なり、いま考えているケースでは、重力もセグメントの動きに影響を及ぼします。したがって、上下方向の並進力がゼロではないというだけでは、上下方向の関節力が発生しているかどうかは、図を見ただけでは判断がつきません(※実際には上下方向の関節力も発生します)。
その一方で、図10をもう一度見てみると、セグメント重心の位置変化は、上下方向だけなく左右方向についても生じていることが分かります。つまり、セグメントに対して左右方向の並進力が作用している(ゼロではない)ということになります。
重力の作用する方向は下方向のみであり、左右方向の成分を持たないので、この左右方向の力の発生源は、セグメントの左端と地面の連結ポイントにおいて作用する関節力(地面反力)以外に考えられません。このように考えてみることで、重力がセグメント重心に作用することによって関節力が発生するということを直観的に理解することができます。
最後に、セグメントの角速度が存在している(ゼロではない)ことによって発生する関節力について考えてみましょう。図11は、1つのセグメントが重心を中心にして一定の角速度で回転している状況を表しています。今回も重力がセグメントの挙動に影響しない状況を考えた方が分かりやすいので、このセグメントは地面に寝かせられているものとしましょう。また、関節トルクも作用していないものとします。

角速度で回転している状況
角速度が一定であるということは、同じ角度だけセグメントの姿勢角が変化するのにかかる時間が等しくなるということを意味します。しかし、図12のように、セグメントの右端の動きに注目してみると、同じ角度変化が生じた時に末端に生じる位置変化の大きさは一定ではないことが分かります。位置変化量が一定ではないということは、速度変化が生じているということであり、速度変化が生じているということは、並進加速度が発生している(ゼロではない)ということになります。

セグメント末端には並進加速度が発生する
セグメント右端の並進加速度がゼロではないということは、もしそこに別のセグメントが連結されていたとしたら、関節トルクによって生じる遠隔的効果について考察したときと同じように、この第2のセグメントは第1のセグメントによって押されたり引っ張られたりするような関節力を受けることになります。
関節トルクが存在せず、重力もセグメントの動きに影響を与えない状況を考えていたので、この関節力の発生原因として考えられるのは、セグメントの角速度が存在する(ゼロではない)ということのみです。このように考えることで、セグメントの角速度が存在する(ゼロではない)ことによって、関節力が発生することを直観的に理解することができます。
3. 拘束のある単一セグメントの運動方程式
本節以降では、運動方程式を変形操作していくことで、全身のセグメントに作用・発生している関節トルク、重力、角速度が、どのように全身の関節力の発生に貢献しているのかを定量する際の基本的考え方について紹介したいと思います。本節では、最も単純で分かりやすい、ただ1つの剛体セグメントが存在し、その片方の端点のみが地面と拘束されているという状況について、どのように方程式を立てれば良いかということについて紹介していきたいと思います。
図13のような状況におけるセグメントの動きを表現するための運動方程式を立てることを考えます。

まず、図14のように、第4回において逆動力学的アプローチによって関節トルクを推定する手法について紹介する際にも立てた3つの式を立てることができます。

加速度・角加速度の関係を表現した3本の方程式
図14で示した3つの式の中には、5つの未知数が存在しています。それに対して、立てられた方程式の数は3本です。第4回においても言及したように、未知数の数と同じだけの方程式を立てることができないと、すべての未知数の値を特定することはできません。
また、図14で示した3つの式のみだと、図13で示した状況におけるセグメントの挙動を完全には表現できていません。何故なら、これら3つの式中のどこにも、セグメントの左端が地面の一点に拘束されて離れることはないという条件が組み込まれていないからです。
そこで、セグメントの左端は点Pから離れることはないということを数式で表現する必要があります。この条件を表現した数式として、セグメントの左端の並進加速度が常にゼロになるという式を立てることができます。具体的な式の形としては図15のようになります。この式は、セグメント同士が自由に動くことが制限されるように「拘束」されていることを表現しているため、拘束式と呼ばれています。

いることを表現した2本の拘束式
セグメント重心に生じるのと同じ大きさの並進加速度aがセグメント末端にも生じるというのはイメージしやすいと思います。角加速度α、角速度ωが式に含まれるのは、前節で紹介したように、セグメント重心を中心とした回転(角加速度、角速度)が発生することによっても、セグメント末端に並進加速度が発生するためです。
4. 変数の置き換えによって連立方程式を解く
2本の並進の運動方程式と1本の回転の運動方程式に加えて、セグメント左端の左右方向、上下方向の位置変化(並進加速度)が常にゼロになることを表現した2本の拘束式の計5つの方程式を立てることができたので、これら5本の方程式を連立して解くことによって、5つの未知数の値を特定することが可能になります。本節では、この連立方程式を具体的に解いていきたいと思います。
まずは、2変数からなる連立1次方程式の解き方について簡単に確認しておきます。x、yの2変数からなる連立1次方程式は、図16のように、片方の変数をもう片方の変数で置き換えていくという手順を踏むことによって、x、yの値を特定することができます。

未知数が3つになった場合であっても、図17のように、ある変数を別の変数で置き換えていくという作業を繰り返すことによって方程式の解を導くことが可能です。

同様の発想、つまり、式を上手く変形操作することによって、ある変数を別の変数で置き換えていくという作業を繰り返すことによって、5つの未知数からなるセグメントの動きを表現するための連立方程式を解くことも可能です。
まず、図18のような式変形を行っていきます。

図19は、図13で値が設定されている文字の値を再掲したものです。これらを式に代入してやることで、5つの未知数の値を順に特定していくことができます。

まず、図18内の式⑩の右辺に含まれる文字は、すべて既に値が決定されているものなので、それらの値を代入して計算することによって、図20のように、角加速度αの値を特定することができます。

続いて、図18内の式⑥⑦の右辺を見てみると、既に値が決まっている変数と、先ほど値が特定された角加速度αによって式が構成されています。したがって、これらの値を代入して計算することで、図21のように、並進加速度$${a_x}$$、$${a_y}$$の値を特定することができます。
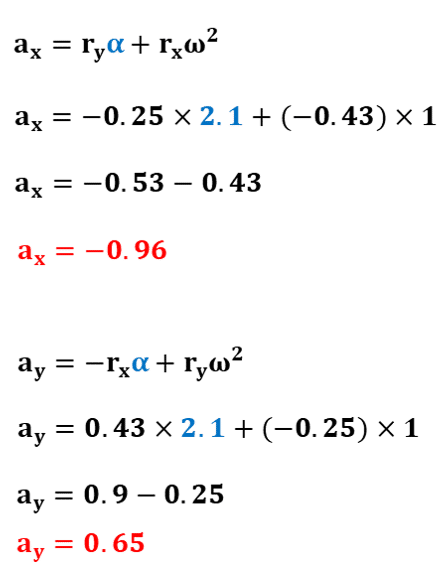
最後に、図18内の式①②の右辺を見てみると、既に値が決まっている変数と、先ほど値が特定された加速度$${a_x}$$、$${a_y}$$によって式が構成されています。したがって、これらの値を代入して計算することで、図22のように、関節力$${F_x}$$、$${F_y}$$を特定することができます。

さらに、前回からの流れを踏まえて、地面との接点でセグメントに作用する関節力(地面反力)$${F_y}$$に対する、関節トルク、重力、角速度それぞれの貢献を定量してみると、図23のようになります。

重力、角速度の貢献
5. 行列を用いて拘束のある単一セグメントの運動方程式を解く
本節では、前節で解いたのと同じ連立方程式を解くための別の方法を紹介します。身体のような多数のセグメントが存在している場合であっても、前節で紹介したような手順によって、未知数の解を求めることが原理的には可能ですが、実際上は膨大な手間がかかってしまいます。
私自身もどれくらい面倒な作業が必要になるのかということをこの場で示すことができると良いかなと思い、連結された2つのセグメントの動きを表現した運動方程式を前節で紹介したのと同じやり方で解くということを試みましたが、あまりにも面倒な式変形が必要になってしまうため、方程式を解ききることを途中で断念してしまいました。たった1つセグメントの数が増えるだけでそうなるので、10数個のセグメントから構成させることが一般的である、身体全体の動きを表現するための運動方程式を前節で紹介した手順で解くことは極めて困難です。
したがって、もっと簡便な方法で多数の式および未知数が含まれる連立方程式を解く方法が必要になります。それが、行列形式で連立方程式を記述して、逆行列を利用して解くという方法になります。本節では、この方法が具体的にどのようなものなのかを紹介したいと思います。
まずは、図24のような、2つの未知数が含まれる簡単な連立1次方程式を題材として、行列を用いて連立方程式を解くということが具体的にはどのような作業かということを紹介したいと思います。

この連立方程式は非常にシンプルなものなので、図25のように、前節で紹介した方法を用いて、x=2、y=4が解であることが簡単に分かります。

2変数からなる連立1次方程式を解く
以下では、行列を用いてこの連立方程式を解いてみたいと思います。図24で示された連立方程式は、行列を用いると、図26のように表記することができます。ここから先に話を進めていく上で、行列同士の掛け算というものがどのような規則に従って行われるかということを最初に確認しておく必要があります。

方程式の行列形式での表現
行列同士の掛け算に関わる規則として、まず確認しておく必要があることは、通常の掛け算では、二つの数の順番を入れ換えても計算結果は変わらないが(交換法則が成り立つ)、行列同士の掛け算の場合は、二つの行列を入れ換えたときの計算結果が一致する保証はない(交換法則が成り立たない)ということです。そのため、ある行列に別の行列を掛ける時には、「左から掛ける」「右から掛ける」という表現が出てくることがあります。
また、行列同士の掛け算は常に行うことができるわけではなく、左の行列の列数と右の行列の行数が一致している場合にのみ掛け算を行うことができます。そして、図27のように、l行m列の行列とm行n列の行列同士の掛け算を行った場合、l行n列の行列が計算結果として出てきます。

次に、行列同士の掛け算を行った結果として出てくる行列の中身がどのようなものになるのかということについても確認しておきましょう。図28のように、行列同士の掛け算を行った場合、出てくる行列のi行j列目の成分は、左側の行列のi行目と右側の行列のj行目の成分を順番にペアを作って掛け算を行い、それらをすべて足し合わせたものになります。

この規則に従って計算を行うことで、図29のように、図26で示された行列を、図24の連立方程式の形に復元することができます。

元の連立方程式が復元できる
次に、行列の形式で表現された連立方程式の解を求める手続きについて紹介します。行列形式で表現された連立方程式の解は、左辺左側の行列の逆行列を両辺に左側から掛けることによって導くことができます。
ここで、「逆行列」とは何かということについて紹介する必要があります。ある行列Xの逆行列$${X^{-1}}$$とは、行列Xに左側から掛けることによって、単位行列が出てくるような行列のことを意味します(図30)。

「逆行列」という聞き慣れない概念を定義するために、「単位行列」というこれまた聞き慣れない概念が出てきてしまいました。そこで、単位行列とは何かということについても確認する必要があります。単位行列とは、行数と列数が等しい行列(これを正方行列と呼びます)で、かつ行列内の行数と列数の値が同じ成分(これを行列の対角成分と呼びます)の値がすべて1であり、それ以外の成分はすべてゼロであるという特徴を持った行列のことを言います(図31)。

単位行列は数字1の行列版とでも言えるような性質を持った行列です。ある数に1を掛けてもその数の値は変化しません。これと同様に、ある行列に単位行列を掛けても、元の行列は変化しません。また、逆行列は数字で言うところの逆数と同じ意味がある行列です。ある数の逆数とは、その数に掛けることで1になるような数のことです。例えば、5の逆数は$${\frac{1}{5}}$$となります。そして、$${\frac{1}{5}}$$は$${5^{-1}}$$と表記されることもあります。ある行列の逆行列もまた、その行列と掛け合わせることによって、「1と同じような性質を持つ」単位行列を作り出すという性質を持っています。行列Xの逆行列が$${X^{-1}}$$と表記されるのは、逆数と逆行列の間に、このような共通性が存在するからだと考えられます。
以上を踏まえて、逆行列を利用して図26の連立方程式を解いてみましょう。左辺左側の行列の逆行列は図32のようになります。実際にこの逆行列と左辺左側の行列を掛け算してみると、単位行列が出てくることが分かります。

続いて、右辺の行列にこの逆行列を左から掛けてみると、図33のように、この連立方程式の解が出てくることが確認できます。

左から掛けると連立方程式の解が導かれる
この解き方も手作業で行うのは大変ですが、幸いにしてコンピュータで自動的に逆行列を算出してくれるプログラムが充実しています。そのため、この形に持ちこんでしまった方が複雑な方程式を解く上でのトータルの手間を大幅に削減することができます。
左端が地面と拘束された単一のセグメントの動きを表現するための連立方程式についても、同じ方法で解くことが可能です。まずは、図34のように、元の5つの方程式について、未知数(並進加速度、角加速度、関節力)が含まれる項を左辺に、それ以外の関節トルク、重力、角速度が含まれる項を右辺に移項します。

それ以外を右辺にまとめる
続いて、図35のように、左辺を2つの行列の掛け算の形に変形します。右側の行列は、5つの未知数を縦に並べた5行1列の行列、左側の行列は、5本の方程式中で5つの未知数についている係数を並べた五行五列の行列となります。
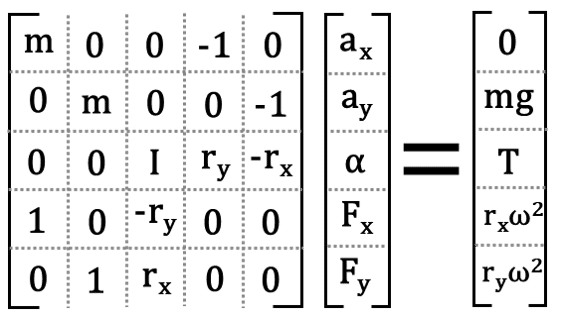
図35の左辺は、先ほど紹介した行列同士を掛け算する際の規則に従って計算をすることで、元の形に復元することができるので、気になる方は図36を確認してみてください。

ことで元の形が復元されることの確認
これで、セグメントの挙動を表現するために必要となる5本の連立方程式を行列形式で表現することができました。したがって、左辺左側の5行5列の行列の逆行列を両辺に左から掛けてやることで、5つの未知数の値を特定することができます。現状では、この行列の中には、m、I、rなどの文字が含まれてしまっているので、まずは図37のように、これらの文字に図13で設定した値を代入します。

その上で、計算ソフトを利用して逆行列を求めると、図38のようになります。
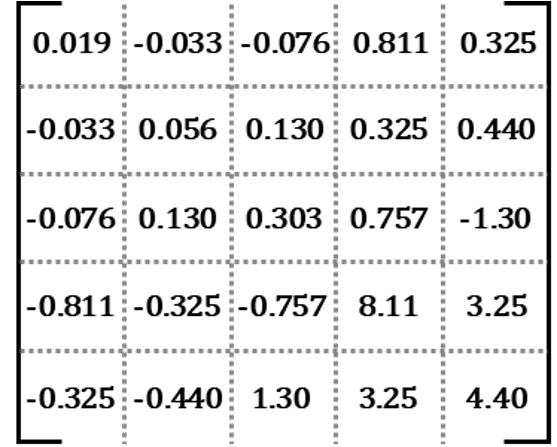
右辺にこの逆行列を掛けた結果を計算してみると、図39のように、前節において算出されたのとほとんど同じ値が出てきます。つまり、前節で紹介した方法であっても、本節で紹介した方法であっても、方法は異なれども、最終的に同じ5本の連立方程式の解を求めることができるということです(細かな数値が異なっているのは、小数点以下の値を適当なところで四捨五入していることによって生じた誤差です)。

6. 行列を用いて拘束のある2セグメントの運動方程式を解く
ここまでは、ただ1つのセグメントのみが存在している状況を想定し、そのセグメントの動きを表現するための運動方程式の立て方、解き方について紹介してきました。実際のバイオメカニクス的動作解析のように、より多くのセグメントが存在している場合であっても、基本的な考え方としては前節で紹介したの変わりなく、方程式の本数や未知数の数が増えるぶんだけ、作業が大変になるだけです。セグメントの数が増えたとしても、基本的な考え方は変わらないのだということを確認するために、本節では、互いに連結した2つのセグメントの動きを表現するための運動方程式を立てて、これを解いてみたいと思います。
図40のような状況について考えることにします。

まずは、個別の方程式を立てます。この2つのセグメントの動きを表現するためには、図41のような10本の方程式を立てる必要があります。

表現するための10本の方程式
一つ一つの方程式が表現している内容については、図41中の赤字で説明されている通りですが、セグメント1と地面との連結を表現した拘束式(7番目と8番目の方程式)と、セグメント1とセグメント2の連結を表現した拘束式(9番目と10番目の方程式)では、右辺の形が違うという点についてだけもう少し詳しく確認しておきたいと思います。
セグメント1の左端は、地面の一点から動かない、つまり、並進加速度はゼロとなるので、7番目と8番目の方程式の右辺はゼロと置くことができます。それに対して、セグメント1の右端およびセグメント2の左端は動くことができるので、並進加速度がゼロになるとは限りません。そのため、セグメント1の右端とセグメント2の左端が連結したまま離れないという条件をどのように数式で表現するのかを考えなければいけません。
どうすれば良いかというと、セグメント1の右端の並進加速度と、セグメント2の左端の並進加速度が常に等しければ、セグメント1の右端とセグメント2の左端は常にくっついたままになります。9番目と10番目の方程式の左辺はセグメント1の右端の並進加速度を、セグメント1の並進加速度、角加速度、角速度を用いて表現したものです。それに対して、右辺はセグメント2の左端の並進加速度を、セグメント2の並進加速度、角加速度、角速度を用いて表現したものです。この2つを等式で結んでやることで、セグメント1の右端とセグメント2の左端が常にくっついて離れない、つまり連結状態が常に維持されるという拘束条件を数式で表現することができます。
式を立てることができたら、残りの手順は、前節で紹介したのと同じです。まず、図42のように、未知数が含まれる項を左辺に、関節トルク、重力、角速度が含まれる項を右辺に集めます。

それ以外を右辺にまとめる
続いて、図43のように、左辺を、未知数を縦に並べた行列とその係数をまとめた行列の掛け算の形に分解します。

そして、図44のように、左辺左側の行列の逆行列を求め、それを両辺に左から掛けます。具体的な計算は割愛しますが、右辺の文字に図40で設定された値を代入した上で、求めた逆行列を左から掛けることで、10個の未知数の値を特定することができます。
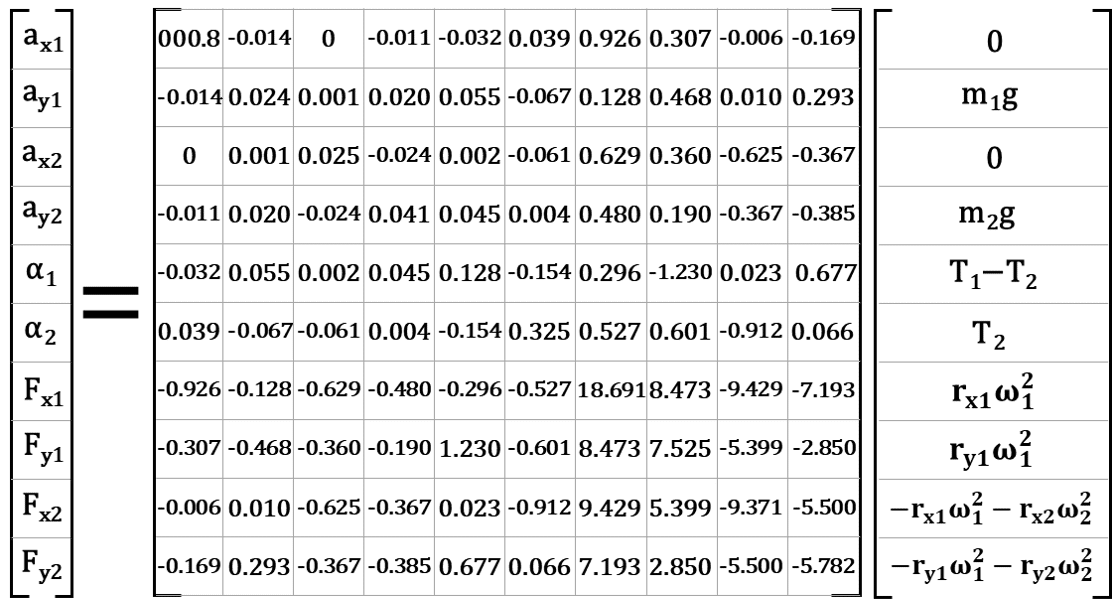
逆行列を両辺に掛ける
最後に、この方程式を利用して、上下方向の関節力の発生に対する、関節トルク、重力、角速度の貢献を定量的に表現するということをしてみたいと思います。ここでは例として、セグメント1の左端と地面との連結ポイントにおいて生じる上下方向の関節力(地面反力)$${F_{y1}}$$に対する貢献について考えてみると、図45のように、それぞれによる貢献量を定量的に把握することができます。

重力、角速度の貢献の定量
7. 動きを表現するための方程式の本数を減らす
前節では、互いに連結された2つのセグメントの動きを表現するために、計10本の方程式を立てました。しかし、実は計2本の方程式のみに集約する形で、実質的には全く同じ状況を表現することも可能です。本節では、どのような考え方をすれば、このような式の立て方が可能になるのかについて紹介したいと思います。
まず、2つのセグメント重心の並進加速度は角加速度と角速度のみを用いて表現することが可能です。具体的には、図46のようになります。

角加速度と角速度を用いて書き直すことができる
セグメント1の重心並進加速度は、セグメント1の角加速度と角速度の組み合わせによって表現されています。このような表現が可能になるのは、図47のように、セグメント1の重心は、左端が地面の1点から動けないように拘束されているために、左端点を中心として重心までの距離を半径とする円周上しか動けないためです。

セグメント1の回転運動によって表現できる
他方で、セグメント2の重心の並進加速度を表現した式の中には、セグメント1の角加速度、角速度だけでなく、セグメント2の角加速度、角速度が含まれた項が存在しています。これは、図48のように、セグメント2の重心位置は、セグメント1の回転とセグメント2の回転の組み合わせによって表現することが可能であるためです。

セグメント1、2の回転運動によって表現できる
以上を踏まえると、図49のように、セグメント重心の並進運動を表現した運動方程式4本、回転運動を表現した運動方程式2本、セグメント重心の並進加速度を角加速度と角速度によって表現した方程式4本の計10本の方程式を立てることができます。

これを、少しややこしいですが、図50のような変形操作をしていきます。そうすることで、最終的に、未知数としてセグメント1、2の角加速度のみを含む2本の方程式にまとめることができます(⑮⑯)。

この二本の方程式を行列形式で書き直すと、図51のようになります。

そして、左辺左側の行列の具体的数値は、図40で設定した数値を文字の部分に代入してやることで、図52のように算出することができます。

文字に数値を代入する
この行列の逆行列は、図53のようになります。

一方で、右辺に含まれる文字にも具体的数値を代入してやると、図54のようになります。

さらに、図55のように、右辺の行列に左辺左側の行列の逆行列を左から掛けてやると、セグメント1、2の角加速度の値を特定することができます。

本節で紹介した式の立て方であっても、表現している運動は、前節で立てた式とまったく同じです。ちなみに、前節の方法で必要だった拘束式が、本節の方法で必要なくなるのは、セグメント重心の並進加速度をセグメントの角加速度と角速度によって表現するということをした段階で、実は既に拘束条件が組み込まれているからです。
表現している運動が同じであることを確認するために、前節の方法、本節の方法それぞれで、角加速度の値、および、それに対する関節トルク、重力、角速度の貢献として出てくる値を比較してみましょう。前節の方法を用いて、セグメント1、2の角加速度の値、および、関節トルク、重力、角速度の貢献を計算してみると、図56のようになります。

それに対する貢献を計算した結果
これに対して、本節の方法を用いて、セグメント1、2の角加速度の値、および、関節トルク、重力、角速度の貢献を計算してみると、図57のようになります。図56と図57の計算結果を見比べてみると、算出される角加速度の値、それに対する関節トルク、重力、角速度の各貢献量の値のどちらについても、ほとんど同じ値が算出されることが分かります。

それに対する貢献を計算した結果
本節の方法では、行列を用いて特定された未知数は2つの角加速度のみであり、セグメントに作用する関節力については、この段階では特定できていません。しかし、特定された角加速度の値を図50の式⑪~⑭に代入してやることで、関節力の値も事後的に特定することが可能です。ここでは、前節と同様にセグメント1に対して地面から作用する関節力(地面反力)$${F_{y1}}$$の値を算出してみます。
計算をしてみると図58のようになります。図57で算出された関節トルク、重力、角速度のそれぞれの貢献量に分解した形で角加速度の値を代入することによって、それぞれの項目ごとの$${F_{y1}}$$への貢献を定量することができます。図58内で示されているように、関節力$${F_{y1}}$$の値、および、それに対する関節トルク、重力、角速度の貢献量のそれぞれが、前節の方法で算出した値とほとんど一致していることが分かります。

対する関節トルク、重力、角速度の貢献の定量
8. 複数の式の立て方が存在する理由
前節および前々節においては、互いに連結された2つのセグメントの動きを表現するための連立方程式を立てる手順として、2つの異なる方法を紹介しました。そして、これらが見た目の式の形こそ異なれども、実質的には同じ運動状況を表現しているのだということを確認しました。
そうすると、結局は同じ計算結果が得られるのに、何故わざわざ2つの方法を繰り返して紹介したのだろうという疑問を持つ方もいるのではないかと思います。そこで、本節では、これら2つの方法を紹介した意図や背景について少しだけお話ししたいと思います。
実は、今回紹介した2つの式の立て方の手順以外にも、様々な方法が存在しています。多数の式の立て方が並存しているのは、式を立てる際の分かりやすさやコンピュータで計算を行う時にかかる時間といった、その方法の良し悪しを評価する際の尺度として複数の観点が存在しており、すべての観点から優れている方法というものは存在せず、どれも一長一短があるからだというのが私の認識です。このような一般論を踏まえた上で、私が今回この2つの式の立て方を紹介した意図についてお話したいと思います。
6節で紹介した方法は、行列の中に含まれている方程式1つ1つの意味が分かりやすいというのが大きな魅力だと私は考えています。つまり、どの部分が一般的な並進運動と回転運動を表現するための運動方程式であり、どの部分がセグメントの拘束条件を表現した拘束式なのかということが非常に分かりやすい構造をしています。
したがって、まず6節の方法を紹介することによって、IAAという解析手法が何か得体の知れない作業を行っているのではなく、拘束条件を加えた上で個別のセグメントの動きを表現した運動方程式を連立して解くということをしているのにすぎないということが理解しやすくなります。6節の内容を紹介せずに、いきなり7節の内容を紹介した場合を想像してみると、IAAとはどのような研究手法であるかということが格段に理解しづらくなってしまうだろうと私は考えています。
それに対して、7節の方法を紹介したのは、冒頭で紹介したIAAの一般式の意味を説明する上で必要だったからです。それは、IAAの一般式として紹介した式は、7節で登場した式を省略表記したものだからです。
まず前提として、そもそも実際にIAAの解析を行う際には、7節で紹介した式の立て方あるいはその亜種が採用されていることの方が多いということをお話しておきます。どうしてそうなるかというと、6節で立てた式と比較すると、7節で立てた式の方が式の規模が小さくなるため、コンピュータを用いて計算を行う際の所要時間が短くなるからです。
今回考えたような、2セグメントのみからなるシステムの特定の一瞬間の動きを計算するのであれば、どちらの方法であっても一瞬で計算が完了するのでこのことの価値は分かりにくいです。しかし、実際のバイオメカニクス的動作解析研究においては、より多くのセグメントが存在する状況について、より長い動作時間について、より多くの回数の試行を対象に、繰り返しこの方法を適用することになります。そうすると、一回の計算を行うのにかかる時間の違いは微々たるものであったとしても、トータルでかかる計算時間には大きな差がつきます。そのため、計算にかかる時間がより短くてすむような形で式を立てておくことに意味が出てくるのです。
以上を踏まえて、IAAの一般式について見ていきましょう。まず、角加速度αは、$${\ddot{\theta}}$$と表記されることもあります。そこで、$${α_1}$$、$${α_2}$$は 、$${\ddot{\theta}_1}$$、$${\ddot{\theta}_2}$$ と表記することにします。そして、$${\ddot{\theta}_1}$$、$${\ddot{\theta}_2}$$を成分とする行列をまとめて$${\ddot{\theta}}$$と表現することにします(図59)。

次に、左辺左側の行列については、作用したトルクが角加速度へと変換される際の抵抗としての意味を持っています。これは慣性モーメントIと類似の性質と言えるので、Iと省略表記します。(図60)
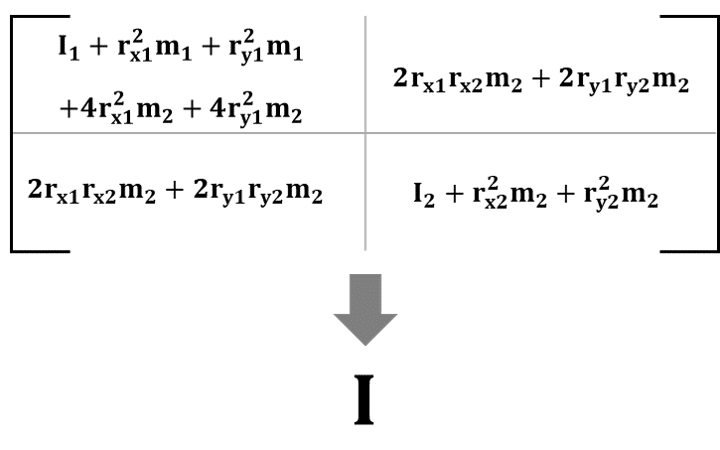
右辺については、図61のように、関節トルクが含まれる項、重力が含まれる項、角速度が含まれる項を分けて書くことができます。これらについてトルク(Torque)、重力(Gravity)、速度(Velocity)の頭文字を採用して省略表記することにします。

以上の省略表記を使用すると、図51で示された式が、図62のような形に書き直されることになります。

最後に、省略表記されているだけで実際には2行2列の行列であるIの逆行列$${I^{-1}}$$を両辺に左から掛けてやることで、冒頭で紹介したIAAの一般式の形になります。このように見ていくと、IAAの一般式として示された謎の記号の連なりの実態が理解可能なものになるのではないかと思います。

9. おわりに
今回は、ある瞬間におけるセグメントの姿勢、関節トルク、重力、角速度が分かっている状態で、セグメント同士やセグメントと地面との連結・拘束関係が表現された形で運動方程式を立ててやり、その連立方程式をなんやかんやして解いてやることで、【関節トルクや重力、角速度】と【関節力や並進加速度、角加速度】との間の因果関係を定量的に評価することができるということをお話してきました。つまり、こうした方法を用いることによって、個別の関節トルク、重力、角速度が存在していることが、個別の剛体セグメントに作用・発生する関節力、並進加速度、角加速度に対してどの程度の貢献をしているかを定量的に比較・評価することが可能になるということです。
特に関節トルクとパフォーマンスとのつながりを定量的に表現できたことによって、身体のどの部位の筋をどのタイミングで活発に活動させることが、パフォーマンス発揮に対してどの程度の重要性を担っているのかをある程度把握できるようになることが期待されます。
今回は、2つのセグメントのみが存在する剛体リンクシステムを例として、かつある一瞬における【関節トルク、重力、角速度】と【関節力、並進加速度、角加速度】との関係性を分析するというところまで紹介しました。実際のバイオメカニクス的動作解析においてこのアプローチを用いるためには、もっと煩雑な作業が必要になりますが、原理的には今回紹介した内容と同じことをしているにすぎません。つまり、拘束条件が組み込まれた形で、より多くのセグメントの動きを表現するための運動方程式を立て、それらを連立して解くということを行えば、全身に作用する関節トルク、重力、角速度の、全身に発生する関節力、並進加速度、角加速度への影響・貢献を定量することができます。
そして、同様の作業を動作を解析する全局面(全フレーム)に対してすべて実行することによって、全動作局面において発生する加速度や関節力に対する、各瞬間に作用する力(関節トルク、重力、角速度が存在することによって作用する力)の貢献をすべて定量することができます。つまり、各瞬間に作用する力がそれぞれ最終的なパフォーマンスにどの程度の影響を及ぼしているのかを定量することができるということです。
この貢献という考え方の妥当性については後々の回で戻ってくることにします。次回は、このIAAの手法を用いて、第1、2回で問題にしてきた、力や行動の目的論的意味を解釈することが可能か否かという点について考察を行っていきたいと思います。
次回
この記事が気に入ったらサポートをしてみませんか?
