
私の幻の博士論文 第5回 力のパフォーマンスへの貢献を定量するという発想-垂直跳び跳躍高を例として-
前回
1. はじめに
前回および前々回では、ある身体の動きを計測し、その情報を基にして、その動きがどのような全身の筋による力(トルク)発揮によって実現されているのかを推定するという作業の概略を紹介しました。そうして得られた解析データと力学についての基本的知識を組み合わせることで、個別の身体セグメントに対して時々刻々に作用した力が、最終的なパフォーマンスにどの程度の貢献をしているのかを定量的に比較・評価が可能になりそうな場合があります。今回は、どのようなロジックに基づいてそうした比較・評価が行なえそうかという点について紹介・考察していきたいと思います。
ところで、上の文章中で私は、「場合がある」「可能になりそう」といった、奥歯にものが挟まっているような表現をしました。「場合がある」という表現をしたのは、今回紹介するアプローチが大きな違和感なく(本当にこのような解析を行って意味があるのだろうかという疑念をあまり抱くことなく)実行できるのは、限られたケースのみだからです。
その「限られたケース」とは、「パフォーマンスの良し悪しを力学的に取り扱いやすい変数で表現できる」という条件が満たされている場合です。このような条件が満たされている場合に限り、その力学的変数(=パフォーマンス)の決定に、個別の身体セグメントに作用する諸々の力がどの程度の貢献をしているのかということを、今回紹介するアプローチによって定量的に比較・評価することが可能になります
また、「可能になりそう」という表現をしたのは、今回紹介するアプローチには、いくつか点で問題(ツッコミどころ)があると私自身は考えているからです。何故問題があると考えているアプローチをわざわざ紹介するのかというと、このアプローチにどのような問題があるのかということを適切に把握するということが、バイオメカニクス的動作解析が上手く行きそうで上手く行かないケースにおいて何が起こっているのかを理解・解明する上で非常に有意義だと考えているからです。そして、問題の所在を突きとめるということは、その状況を打開するためにはどのような手を打つべきなのかを考える上での足掛かりにもなるのではないかと思います。
どのような問題点があるのかということは本連載全体を通じて考察していく予定です。そのための準備として、「そのアプローチが基本的にはどのようなもの(だと私が理解している)か」という点について、読書の皆様との間で共通認識を形成しておくことが、今後の議論を円滑に進める上での助けとなるのではないかと考えています。これが今回の内容の連載全体の中に占める意義ということになります。
パフォーマンスを力学的変数と直接的に結びつけることが容易な運動課題の典型例として垂直跳びが挙げられます。垂直跳びのパフォーマンスとは単純明快に跳躍高であると言って良いでしょう。さらに、詳しくは次節にて紹介しますが、跳躍高の定義の仕方によっては、ある単一の力学的変数のみが、跳躍高(パフォーマンス)の決定に影響していると考えることが可能になります。
そこで次節以降では、スクワットジャンプと呼ばれる、膝を曲げた静止姿勢から開始する反動なしの垂直跳びを題材として、ある運動課題のパフォーマンスを、別の力学的変数と結びつけるという考え方、及びその力学的変数に対する個別の力の貢献を定量的に比較・評価するという考え方について紹介していきたいと思います。
2. 垂直跳び跳躍高と離地時重心上向き速度の関係
本節では、垂直跳びの跳躍高についてのより厳密な定義を導入した上で、その定義に基づくことで、垂直跳びの跳躍高が「離地瞬間における重心の上向き速度」というただ一つの力学的変数のみによって決定されていると考えることが可能になるということをお話しします。
垂直跳びは、跳躍高の大小という極めて単純で明瞭な単一の指標によってパフォーマンスの高低を数量的に比較・評価することが可能です。しかし、跳躍高という一見すると意味の揺らぎがなさそうな概念であっても、実は複数の定義の仕方をする余地があります。一例としては、図1左のように、直立して手を上に挙げたときの指高と空中で腕を上に伸ばしたときの最高到達点の差によって跳躍高を定義するということもできるでしょう(定義A)。それに対して今回採用する跳躍高の定義は、図1右のような、「離地瞬間における重心高と重心の最高到達高の差」というものです(定義B)。

複数の選択肢が存在する
定義Bには、力学的な解析を行う際に取り扱い易いという利点があります。なぜなら、本節冒頭で述べたように、定義Bを採用することで、跳躍高を「離地瞬間における重心の上向き速度」という、単一の力学的変数と結びつけることが可能になるからです。このことは、図2のように力学的エネルギーの保存則から導くことができます。

重心の上向き速度のみとなる理由
定義Bを採用した場合、跳躍高を変化させ得る変数が「離地瞬間における重心の上向き速度」のみとなるということは、身体が地面から離れた後にどのように足掻こうとも、重心の最高到達点(つまり、定義Bにおける跳躍高)は変化させられないということを意味します。そのため、ある力がどの程度垂直跳びのパフォーマンス(跳躍高)に貢献しているのかという問題は、その力が離地瞬間における重心の上向き速度の発生にどの程度貢献しているのかという問題に置き換えることが可能になります。
それに対して、定義Aを採用した場合は、空中でタイミングよく腕を上に伸ばすことができるか否かによって跳躍高が変動してしまいます。そして、このようなタイミングの良し悪しが絡むような問題を力学的な解析においてどのように取り扱えば良いのかというのは、確固たる答えが非常に出しづらいものです。このような理由から、今回は定義Bを採用して話を進めさせていただきます。
3. ターン制マス目移動モデルによるセグメント重心の位置、速度、加速度の表現
前節では、垂直跳びの跳躍高についてのより厳密な定義(跳躍高=離地瞬間における重心高と重心の最高到達点の差)を導入した上で、その定義に従うことで、跳躍高への貢献を評価するということを、「離地瞬間における重心の上向き速度」への貢献を評価するということに置き換えられるということをお話ししました。それを踏まえて、本節以降では、
①「離地瞬間における重心の上向き速度」に対する「離地瞬間における個別セグメント重心の上向き速度」の貢献の定量的評価(4節)
②「離地瞬間における個別セグメント重心の上向き速度」に対する「動作開始から離地までの間において当該セグメント重心に発生した上向き加速度」の貢献の定量的評価(7節)
③「各瞬間において発生した個別セグメント重心の上向き加速度」に対する「当該瞬間において当該セグメントに作用した個別の力」の貢献の定量的評価(8節)
という三つのステップを踏むことで、時々刻々において個別の身体セグメントに対して作用した力の跳躍高(パフォーマンス)への貢献を定量的に比較・評価することが可能になるということをお話ししたいと思います。
本節では、そのための準備として、このような作業手順の概略を直観的に理解することの助けとなるようなモデルを導入したいと思います。このモデルのことを「ターン制マス目移動モデル」と呼ぶことにします。
図3のように、複数のマス目が縦に並んでおり、ターンが来るたびにそのマス目を黒丸が移動していくという状況について考えます。

図4のように、黒丸はある一つのセグメントの重心位置を抽象的に表現したものだと考えてください。マス目が縦一列に並んでいるのは、(垂直跳びにおける跳躍高と直接関係する)上下方向の移動についてのみ考えるということと対応しています。

抽象的に表現している
ターンごとに黒丸が移動するというのは、動作解析を行うフレームごとにセグメント重心位置が移動していくということと対応しています。実際の動作解析においては、数100フレーム分の解析を行うこともしばしばありますが、以下では単純化のため全4ターン(4フレーム)によって運動が完結するという設定で話を進めることにします。
このモデルと実際の動作解析の間には、図5にまとめたような違いがあります。しかし、その違いは要素の数が増えたり、より細かな数値表現を行なったりする場合があるといった点についてのものです。そうした数量的な多さや細かさを取り払った際の、バイオメカニクス的動作解析におけるセグメント重心の挙動を記述するということの本質という点では、このターン制マス目移動モデルによって表現できていると考えてしまって差し支えありません。

現実の動作解析の相違点
次に、この全4ターンからなるターン制マス目移動モデルにおいて、黒丸の速度、加速度を表現するということについて考えてみましょう。図6のように各ターンにおける黒丸の位置が変化していったとしましょう。このとき、各ターンにおいて何マス分の移動(位置の変化)が起こったのかということを考えることができます。

図6のケースでは、1ターン目においては位置0から位置3までの+3の変化、2ターン目においては位置3から位置7までの+4の変化が起きています。この各ターンにおいて何マス分の移動(位置変化)が生じているのかということが、単位時間あたりの移動量(位置変化)である速度と対応していると考えることができます。
さらに、図7のように、あるターンにおいて移動するマス目の数が、前のターンにおいて移動したマス目の数と比較してどの程度増減したのかということを考えることもできます。

おける加速度の表現
例えば、初期状態では黒丸は止まった状態だったとすると、1ターン目における前のターンからの移動マス数の増減は+3となります。さらに、2ターン目以降は、+1,+1、+2といった具合になります。この各ターンにおいて前のターンと比較して移動するマス数がどのように変化しているかということが、単位時間当たりの「位置変化の変化」を意味する加速度と対応していると考えることができます。
このような見方をすることで、ある一つのセグメント重心の上下方向の位置、速度、加速度が解析フレームごとに変化していく様子を単純化した形で捉えることが可能になります。
4. 重心(全体)速度に対するセグメント(部分)速度の貢献
本節では、
①「個別のセグメント重心の上向き速度」から、「身体全体の重心の上向き速度」を算出する手順
について紹介した上で、
②「個別のセグメント重心の離地瞬間における上向き速度」の「身体全体の重心の上向き速度」に対する貢献
を定量的に表現する際の考え方について紹介したいと思います。
ここまで重心速度とは何かということについてぼやかしたまま話を進めてきました。そこで、まずはセグメントの重心速度から身体全体の重心速度を算出する際の手順について確認しておきたいと思います。
重心速度とは、身体を構成している複数のセグメントごとの重心速度をセグメントごとの質量の違いを考慮して平均したものと言えます。具体的には、
①セグメントごとに質量と重心速度を掛け合わせる
②それらをすべて足し合わせる
③全体の質量で割る
という計算手順によって算出することができます。図8は、単純なケースとして、2つのセグメントそれぞれの重心速度から全体として重心速度を算出する手順を示したものです。

全体としての重心速度を算出する手順
さらに、この計算式を図9のように変形してみると、離地瞬間における重心(身体全体としての)の上向き速度に対する、個別のセグメント重心の上向き速度の貢献を分解的に表現することができます。

速度の貢献の定量方法
5. 過去の加速度は現在の速度に影響を及ぼすことができるのか?
7節では、離地瞬間におけるセグメント重心の上向き速度に対する、動作開始から離地瞬間に至るまでの時々刻々(各フレーム、各ターン)においてセグメント重心に発生した加速度の貢献を定量的に評価する際の基本的考え方を紹介します。本節および次節では、その前段階として、ある時点における速度に対する「それ以前の時点において」発生した加速度の貢献というものが存在し得るためには、ある前提条件が必要になるという考察をしたいと思います。
その前提条件とは、「ある時点で発生した加速度の影響は、その後の時点においても速度のレベルで残存し続ける」というものです。この前提条件が成立しているか否かという点が、実は必ずしも明らかではないというのが、本節および次節で考察する内容となります。やや脱線し過ぎの感もありますが、重要かつ知的に面白い論点ではないかと思うので、お付き合いいただけますと幸いです。
まずは、「ある時点における速度に対するそれ以前の時点において発生した加速度の影響」を定量的に評価するというのが、具体的にはどのようなことをしようとしているのかという点について簡単に確認しておきたいと思います。図10は、図6で例示した4ターンを通じた黒丸の移動のうち、2ターン目までを取り出したものです。ここで2ターン目における黒丸の移動マス数(速度)に対する1ターン目と2ターン目の移動マス数の増減(加速度)の貢献について考えてみます。
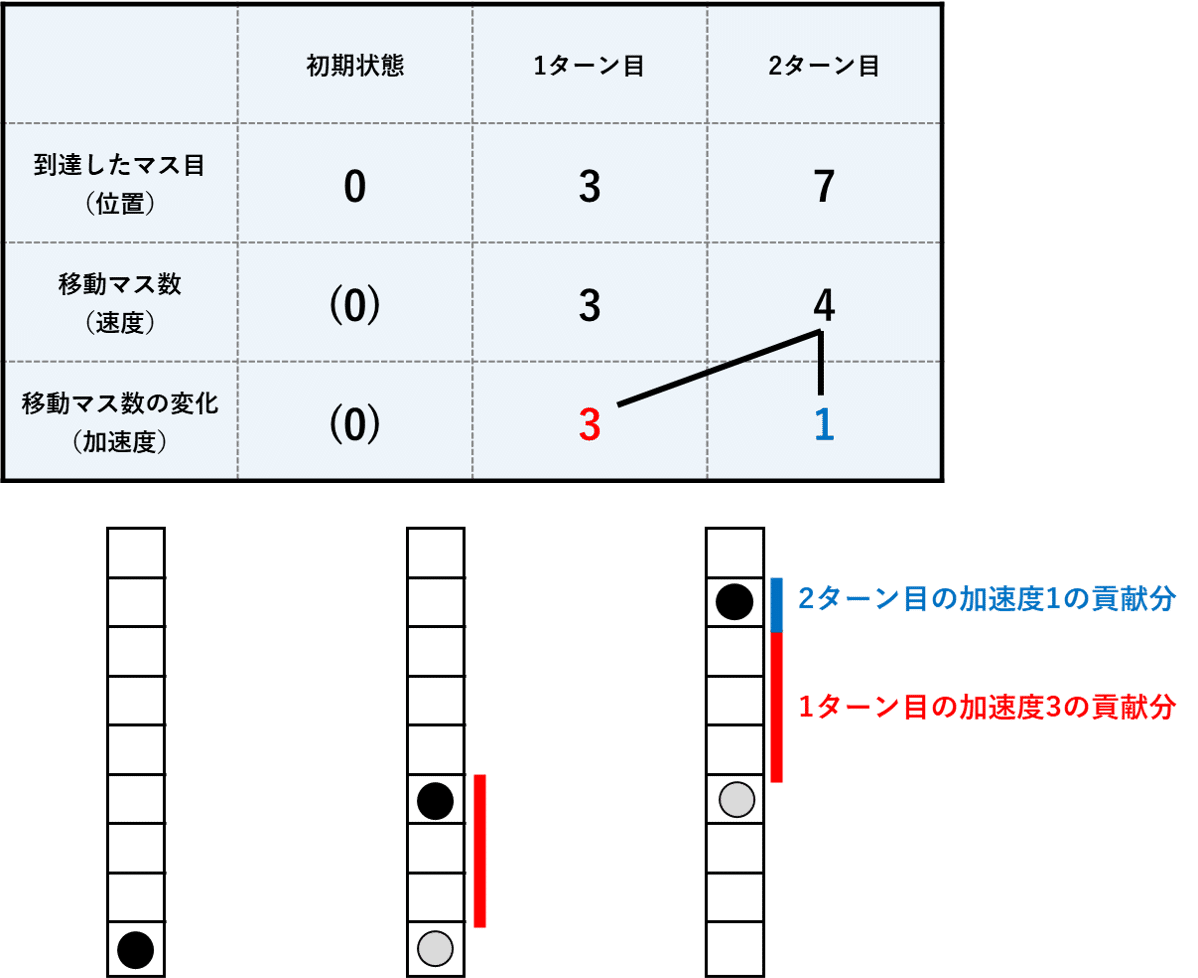
2ターン目の加速度が影響している?
7節で紹介するのは、2ターン目における+4という移動マス数(速度)のうち、75%は1ターン目における移動マス数の変化(加速度)+3の貢献分であり、残りの25%が2ターン目における移動マス数の変化(加速度)+1の貢献分であると解釈するという考え方です。
このような解釈に対しては、妥当なものであると直感的に感じる人もいれば、違和感を持つ人もいるのではないかと思います。この解釈に妥当性を感じるのは、それぞれのターンにおける移動マス数の変化(加速度)を足し合わせたものが、2ターン目における移動マス数(速度)の値とぴったりと一致するからではないかと私は考えています。
他方で、1ターン目に3マス進んだ後は、そこで一旦停止して、2ターン目に再び動き出して4マス進んでいるのだというような見方をしてみると、2ターン目に4マス移動した(+4という速度を持っていた)ことに1ターン目の出来事が貢献(影響)していると解釈するのはおかしいのではないかと主張することもできそうです。
後者の主張に対しては、これは単にターンごとにマス目を移動するというモデルで現実の連続的なセグメントの動きを表現していることに起因する歪みなのではないかという反論が出てくるかもしれません。しかし、私はこのような主張にはそれ以上の重要な意味があると考えています。そこで以下では、この論点についてさらに踏み込んだ考察をしてみたいと思います。
3節においてターン制マス目移動モデルを導入した際には、各ターンにおいて黒丸が移動するマス数について、何も決まり事を設けていませんでした。ここで、各ターンにおける黒丸の移動マス数を決定する規則として、二つの候補(規則A、規則B)を提示してみたいと思います。
2つの規則では共に、各ターンにおいて100円を最小単位としたお金が支払われ、支払われた金額に応じて移動するマス数が決定されます。
規則Aでは、それまでの全てのターンにおいて支払われた総額を基準として、100円あたり1マスの比率で、そのターンにおける移動マス数が決定されるものとします。例えば、2ターン目においてそれまでに(1ターン目と2ターン目で合わせて)支払った総額が100円だったら1マス進み、500円だったら5マス進むといった具合です。
規則Aの下で図10における黒丸の移動パターンが再現されるのは、図11のように、1ターン目に300円が支払われ、2ターン目に100円が支払われた場合ということになります。このケースでは、2ターン目における4マスの移動のうち3マス分は、1ターン目に300円が支払われたことによる効果が2ターン目においても引き続き有効であることによるものだと解釈することができそうです。

影響が後のターンにおいても残存する
これに対して、規則Bでは、そのターンにおいて支払われた金額のみを基準として、100円当たり1マスの比率で、そのターンにおける移動マス数が決定されるものとします。例えば、2ターン目に支払った金額が300円だとしたら、1ターン目にいくら支払ったのかに関わりなく、必ず3マス移動するということになります。
規則Bの下で図10における黒丸の移動パターンが再現されるのは、図12のように、1ターン目に300円が支払われ、2ターン目に400円が支払われた場合ということになります。このケースでは、2ターン目における4マスの移動は、すべて2ターン目に400円が支払われたことによるものだと解釈するべきでしょう。

おける出来事の影響は消失する
6. 運動の第1、第2法則との関係から考える
前節では、ターン制マス目移動モデルにおいて、各ターンにおける黒丸の移動マス数が決定される規則として2つの候補を提示しました。本節では、私たちの住んでいる現実世界の物理法則(物体の運動を決定する規則)が規則A、規則Bのどちらに似ているかということを考えてみたいと思います。ある時点における速度に対して、それ以前の時点において発生した加速度が影響(貢献)しているという解釈が可能になるためには、私たちの住んでいる現実世界の物理法則が規則Aに似ている必要があります。
既に察しがついている方もいるのでないかと思いますが、このモデルにおいてお金が支払われるということは、現実世界においては物体に力が作用するということと対応しています。そこで、お金が支払われる(=物体に力が作用する)ということと、ターンごとの黒丸の挙動(物体の位置、速度、加速度)との間にどのような関係性が成立しているかという観点から、私たちの住む現実世界の物理法則と規則A/Bとの類似性について考えてみたいと思います。
ニュートン力学には運動の3法則と呼ばれるものが存在します。以下では、このうち第1、第2法則と規則A/Bの関係性について考察していきます。
第1法則は慣性の法則とも呼ばれています。慣性の法則とは、物体に外部から力が作用していない場合、止まっている物体は止まり続け、ある速度で動いている物体はその速度で動き続けるというものです。
第2法則は、物体に力が作用すると、その力の大きさに比例した加速度が物体に生じるというものです。この原理を数式によって表現したものが運動方程式F=maであると説明されることもあります。
以上を踏まえて規則A/Bとこれらの物理法則との関係性について考えてみましょう。
まずは第1法則(慣性の法則)との関係性について見ていきましょう。規則Aでは、あるターンにおいて支払われた金額(作用した力)がゼロであったとしても、そのターンにおける移動マス数(速度)はゼロにならず、一つ前のターンにおける移動マス数が維持されます。それに対して、規則Bでは、あるターンにおいて支払われた金額(作用した力)がゼロの場合は、そのターンにおける移動マス数(速度)もゼロになります。このように比較してみると、規則Aは慣性の法則が成立している世界と類似の性質を持っていることが分かります。
次に、第2法則との関係性についても見ていきましょう。規則Aにおいては、あるターンにおいて支払われた金額(作用した力)が直接的に変化させているのは、一つ前のターンからの移動マス数の変化(加速度)であり、それが変化することによってそのターンにおける移動マス数(速度)が間接的に変化するという構造をしています。他方で、規則Bにおいては、あるターンにおいて支払われた金額(作用した力)によって、そのターンにおける移動マス数(速度)が直接的に変化させられるという構造をしています。このように整理してみると、第2法則との関係という観点からも、規則Aは私たちの住んでいる現実世界の物理法則と似た性質を有しているのに対して、規則Bはそうではないということが分かります。
このように私たちの住んでいる現実世界の物理法則は、規則Aと類似の性質を有しています。だからこそ、ある時点において発生した加速度が、それ以後の時点における速度の中に影響を残しているという見方が可能になるのです。
7. 離地瞬間の速度に対するそれ以前の加速度の貢献を定量する
前節における考察から、離地瞬間における重心の上向き速度に対する、それ以前に生じた加速度の貢献(影響)というものが存在すると考えても良さそうだということが確認できました。そこで本節では、ターン制マス目移動モデルを活用して、身体各セグメントに対して時々刻々に発生する上向き加速度の、離地瞬間における重心の上向き速度に対する貢献というものがどのように定量的に比較・評価されるのかという点について、その概略を紹介したいと思います。
図13のように、2つの黒丸が4ターンに渡ってマス目を移動していく状況を例題として考えてみましょう。最終4ターン目における移動マス数を2つの黒丸の質量の違いを考慮して平均したものが、離地瞬間における重心の上向き速度に相当するものと解釈できます。便宜上これを「黒丸全体の最終速度」と呼ぶことにします。

まずは、4節において紹介した方法で、黒丸全体の最終速度に対する、黒丸1、黒丸2それぞれの最終速度(4ターン目の移動マス数)の貢献を定量します。結果としては、図14のように、黒丸全体の最終速度6.8のうち3.2(約47%)分が黒丸1が持っている速度による貢献、3.6(約53%)分が黒丸2が持っている速度による貢献ということになります。

最終速度の貢献分に分解する
次に、各ターン(各時点、各フレーム)における各黒丸の加速度(前のターンからの移動マス数の変化)が、黒丸全体の最終速度にどの程度の貢献をしているのかを定量してみましょう。これは図15のように、各ターンにおける加速度(前のターンからの移動マス数の変化)が、最終ターンにおける速度(移動マス数)のうち何%分を占めているのかを計算し、それと黒丸ごとの全体の最終速度への貢献割合の値を掛け合わせてやることで算出することができます。

全体最終速度に対する貢献割合の算出
さらに、図16のように棒グラフ化することによって、4ターンを通して2つの黒丸それぞれに発生した加速度が、どの程度黒丸全体の最終速度に貢献しているのかを視覚的に表現することもできます。

最終速度への貢献割合の視覚化
8. 加速度に対する力の貢献を定量する
前節では、離地瞬間における重心の上向き速度に対して、動作開始から離地瞬間に至るまでの時々刻々における個別セグメントごとの加速度がどの程度貢献(影響)しているのかを定量する方法について紹介しました。最後に本節では、個別の瞬間(フレーム、ターン)において発生した加速度に対する力の貢献を定量するということについて紹介したいと思います。
セグメントの上向きの加速度と関係するのは、そのセグメントに作用している上下方向の力です。前回の確認になりますが、あるセグメントの上下方向の運動を表現するための運動方程式は、シンプルな形としては図17のようになります。

並進運動を表現するための運動方程式
Fyは、このセグメントに作用する全ての上下方向の力を合算したものです。そして、これも前回の確認になりますが、この合算された力を、複数の力の発生源ごとに分けて捉えることも可能です。典型的には、図18のように、セグメントの両端点に作用している関節力と、セグメントの重心に一括して作用していると考えることが計算上可能な重力の三つの力に分解して考えることが可能です。

力を3つの発生源に分ける
ここで、分解された3つの力が一つずつ作用したとしたら、セグメントにどのような加速度が発生するのかということを考えることができます。例えば、セグメントの質量、作用する力の大きさが図18のような条件では、図19のように、セグメント上端に作用する関節力によって$${−20 m/s^2}$$の加速度が、下端に作用する関節力によって$${+40 m/s^2}$$の加速度が、重力によって$${−10 m/s^2}$$の加速度がそれぞれ発生させられ、それらが合計されることで、その瞬間に実際に目に見える形で発生する加速度($${+10 m/s^2}$$)が発生していると考えることができます。

貢献している加速度の算出
最後にターン制マス目移動モデルでこの点についてまとめてみましょう。実際の身体運動においてセグメントに作用する力には、マイナスの(垂直跳びの場合は下方向への加速度の発生に対する)貢献をしている力というものが不可避的に含まれます。重力は常に下向きの加速度を発生させるような影響を各セグメントに対して及ぼしています。また、作用反作用の法則が存在するため、ある関節で片一方のセグメントに対して上向きの関節力が作用している場合には、もう一方のセグメントに対しては下向きの関節力が作用することになります。
かなり細かい論点になってしまうので、今回は考察しませんが、このようなマイナスの貢献がある場合は、最終パフォーマンスに対する貢献を割合として分かりやすく把握するのが難しくなってしまいます。そこで以下では、各セグメントに対しては、二つの力の発生源(お金の支払元)のみが存在し、それらはプラスの加速度のみを発生させるというように状況を単純化して考えることにします。
図20は、図13の状況に、各ターンにおいて支払われた金額は二つの支払元(α、β)が支払った金額が合算されたものであるという設定を追加したものです。例えば、1ターン目における黒丸1に対する支払総額100円は、支払元αからの60円と支払元βからの40円が合計されたものになります。二つの支払元からの支払いを合算したものが、そのターンにおける各黒丸に対する支払いの総額となるというのは、二つの発生源から作用した力を合算したものが、その瞬間における各セグメントに作用する力の合計になるということと対応しています。

速度への貢献の定量
図20における支払い金額についての分割の設定を踏まえると、各ターンにおいて各黒丸に対して各支払元から支払われた金額(各瞬間・フレームにおいて各セグメントに対して各力発生源から作用した力)が黒丸全体の最終速度(離地瞬間における重心の上向き速度)に対して何%分の貢献をしているのかを計算することが可能になります。
具体的な計算手順としては、図15、16で算出された「各ターンにおいて各黒丸に発生した加速度の、黒丸全体の最終速度に対する貢献割合」と、支払元α、βが支払った金額の全体(α+β)に占める割合を掛け算してやれば良いです。例えば、1ターン目において黒丸1に対して支払元αから60円が支払われたことは、黒丸全体の最終速度のうち10.6%分の発生に貢献しているということになります。
9. おわりに
以上のような考え方をすることによって、時々刻々において身体各セグメントに対して作用する個別の力が、垂直跳びのパフォーマンス(跳躍高)実現に対してどの程度の貢献をしているかという点について、定量的に評価・比較することが可能になります。今回の内容をまとめると図21のようになります。
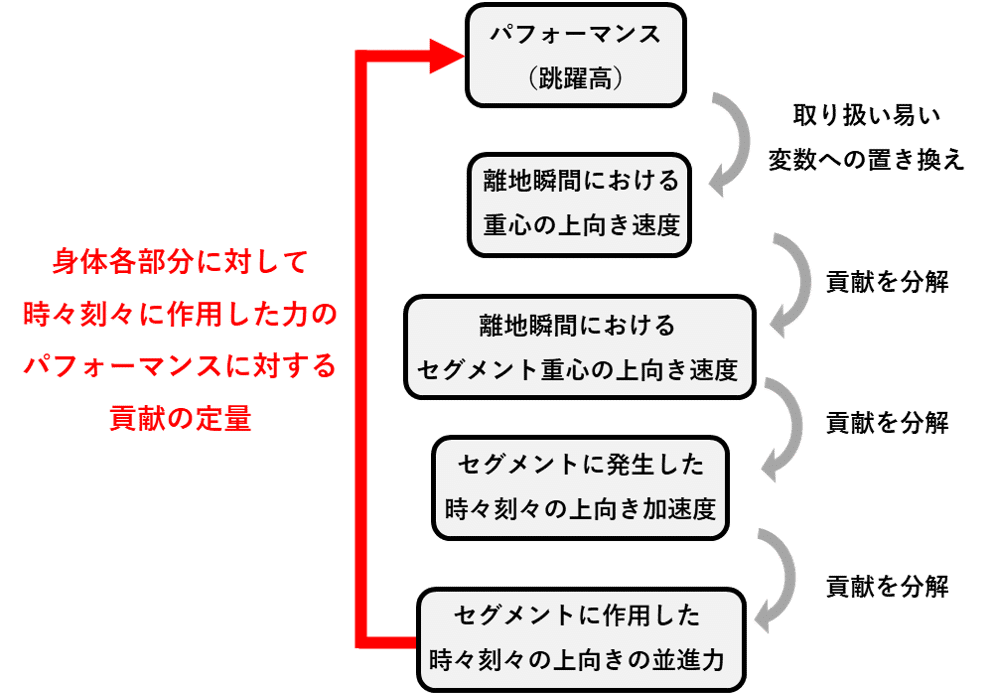
このような解析を行うことによって、どのタイミングでどこに働いている力が、パフォーマンスの実現に対してどの程度の重要性を担っているのかをある程度把握することができます。しかし、実は今回紹介した内容のみでは、ある種の行き詰まりが生じてしまいます。次回は、この行き詰まりとはどのようなものかということについて考察した上で、その問題を解消してくれそうなアプローチとして、ここ20年くらいの間、バイオメカニクス的動作解析研究の領域において注目を浴びてきた研究手法について、その概略を紹介したいと思います。
次回
この記事が気に入ったらサポートをしてみませんか?
