
私の幻の博士論文 第4回 身体の動きを記述する方法:逆動力学的アプローチによる関節トルクの推定
前回
1. はじめに
前回は、モーションキャプチャ―によって取得される、全身に貼りつけられたマーカーの位置情報を基にして、分析対象とする全撮影フレームにおける、重心やセグメント同士の連結点(関節中心)の位置、重心の速度・加速度、セグメントの姿勢角とそれを微分していくことで得られるセグメントの角速度・角加速度などを算出するという作業について、その概略を紹介しました。今回は、これらのうち、加速度、角加速度、関節位置についての情報を用いて、全身の各セグメントに作用している力(並進力)やトルク(回転トルク)を算出する手順について紹介したいと思います。
剛体セグメントに作用する力(並進力)とは、剛体の重心位置の上下左右方向への加速度を発生させる力学的原因と言えるようなものです。それに対して、剛体セグメントに作用するトルク(回転トルク)とは、剛体に角加速度を発生させる力学的原因と言えるようなものです。
※ここで、「と言えるようなもの」というやや曖昧な表現をしているのは、より深く考えていくと、「力は本当に加速度の原因と言えるのか?」や「そもそも力は本当に実在しているものなのか?」といった論点が存在し、そのため、「力=加速度発生の原因」と単純に言い切ってしまうのは語弊があると私自身は考えているからです。ただし、読者の方々は、さしあたりは「力=加速度発生の原因」という認識で読み進めていただいた方が、混乱せずにすむと思います。
力やトルクを算出するためには、力と加速度、トルクと角加速度の関係を表現した数式である運動方程式を立てる必要があります。力・トルクの値が先に特定された後に、そのような力・トルクが作用している場合に発生する加速度を算出することを「順動力学計算」と言います。反対に、加速度・角加速度の値が先に特定された後に、そのような加速度・角加速度が発生している場合に作用している力・トルクを算出することを「逆動力学計算」と言います。
バイオメカニクス的動作解析における標準的(基本的)研究手法として教科書などで広く普及しているのは、後者のように先に加速度・角加速度の値を特定してから、その情報を基に力・トルクを推定するというものです。そのため、こうした研究手法は「逆動力学的アプローチによる力・トルクの推定」などと呼ばれています。
2. 単一剛体の二次元運動方程式 ①並進力と加速度の関係性を表現した式
物体に作用する力と発生する加速度の関係についての方程式F=maというものをご覧になったことがある方も多いと思います。Fは物体に作用する力(Force)、aは物体に生じる加速度(Acceleration)、mは物体の質量(Mass)をそれぞれ意味しています。つまり、F=maとは、物体に作用している力Fの値は、物体の質量mと物体に発生している加速度aを掛け算した値と同じになるということを表現したものなのです。
セグメント重心の加速度aの値は、前回紹介した方法を用いることで推定することができます。したがって、後はセグメント質量mの値が分かれば、セグメントに作用する力Fの値を特定することができます。例えば、mは10 (kg)、aは20 (m/s2) という値だとすると、F=10×20=200 (N:ニュートン) ということになります。
前回、セグメントの重心位置がどのあたりに存在するかは、そうした問題を専門的に扱っている研究論文において記載されている値を根拠として推定するということをお話ししました。実は、セグメントごとの質量や、次節紹介するセグメントごとの「慣性モーメント」と呼ばれるものも、たいていは同じ研究論文内で検討されています。そこでは、セグメントの質量については、体重(全身の総質量)の何%といった形で示されています。
前回参照した阿江通良・藤井範久『バイオメカニクス20講』の41ページに載っている資料には、セグメントごとの体重に対する相対質量もまとめられており、例えば、下腿セグメントは体重の約5%の質量を持つとされています。つまり、例えば、体重70kgの人の場合、片方の下腿セグメントの質量は、3.5kgということになります。
このような研究資料に依拠することによって、個別の動作解析研究の場面においては、モーションキャプチャ―の対象となる各個人ごとの体重のみを測っておけば、その人のセグメントごとの質量の推定値を簡単に決定することができます。
※前回もセグメントの重心位置を推定するということとの関連でお話ししましたが、個人ごとの体型の違いなどによって、個々のセグメントの体重に対する相対質量の値は、厳密には人それぞれ異なります。したがって、セグメント質量の値についても、セグメントの重心位置と同様に、あくまでも大まかな推定値であるということは留意しておく必要があります。
以上のように、バイオメカニクス的動作解析研究においては、セグメントの質量mは、他の研究論文からの情報と個々人の体重から推定値を割り出すことができ、セグメント重心の加速度aは、モーションキャプチャ―によって記録したマーカーの位置座標データに対して二回の微分計算を行うことによって算出できます。つまりこの段階で、F、m、aのうち二つ(mとa)について、その値を特定(推定値を決定)できていることになります。この状態に持ち込むことができれば、残った一つの未知数Fの値を簡単な計算によって特定することができます。これが、バイオメカニクス的動作解析における基本的研究手法である、計測した動作レベルの情報を基にして、運動中の身体各セグメントに作用している力・トルクを推定するという手続きが行っている内容についてのシンプルな説明です。
ここで質量mの力学的意味について考察しておきます。この点についてお話しておくことで、次節で紹介する慣性モーメントと呼ばれるものが何を表現したものなのかが理解しやすくなると思います。
質量mとは、物体に力が作用することによって物体が動かされようとする際に、加速度の発生を妨げる抵抗の大きさを表した量だと言えます。大きな質量を持つ(重い)物体は、加速させづらく(逆に言うと、物体が大きな速度を持っている場合は減速・停止させづらく)、反対に、小さな質量の(軽い)物体は、加速(または減速)されやすいということです。
運動方程式F=maにいくつかの値を試しに入れてみると、このことがよく分かります。例えば、F=100という力をm=1という質量の物体に作用させた場合はa=100という加速度が発生することになります。それに対して、同じF=100という力をm=50という質量の物体に作用させた場合は、a=2という加速度が発生します。このように、作用する力Fの大きさが同じであっても、質量mが大きい方が、発生する加速度aは小さくなります。
一つの剛体セグメントの重心の加速度は、二次元平面の動きのみを考える場合、水平(前後もしくは左右)方向と上下方向の二つの軸に分解して記述・表現する必要があります。したがって、前回同様に水平方向をX軸、上下方向をY軸とすると、下のように、それぞれの方向ごとの力と加速度の関係を記述・表現するための二本の運動方程式を立てることができます。
F_x=ma_x
F_y=ma_y
3. 単一剛体の二次元運動方程式 ②回転トルクと角加速度の関係性を表現した式
前回からしてきた話を踏まえることで既に想像がついている方もいるかもしれませんが、この二つの方程式だけで、二次元平面上での剛体の運動を記述・表現しきれるかというと、これだけでは不十分です。一つの剛体の二次元平面上における動きを記述・表現するためには、重心の並進の動き(加速度)に加えて、姿勢角、つまり回転の動き(角加速度)についても考慮する必要があるからです。
剛体の回転運動の原因となるトルクと、それによって発生する角加速度の間で成立する関係についても、力と加速度の関係と似たような数量的法則性が存在します。それを表現した数式が、回転運動についての運動方程式N=Iαというものです。
Nは剛体に作用しているトルクを、α(アルファ)は剛体の角加速度を、Iは剛体の慣性モーメント(Inertia moment)をそれぞれ意味しています。トルクNは、並進運動についての運動方程式における力Fと似たような意味を持っています。冒頭で言及した内容の繰り返しになりますが、力Fは剛体重心に並進加速度が発生することの原因となる作用であるのに対して、トルクNは剛体に角加速度が発生することの原因となる作用ということになります。
慣性モーメントIは、物体の回転のしづらさ(角加速度発生に対する抵抗の大きさ)を表した量であり、並進運動についての運動方程式における質量mと似たような意味を持っています。つまり、同じ大きさの力Fが作用した場合には、質量mが大きい方が発生する加速度aが小さくなるのと同様に、同じ大きさのトルクNが作用した場合には、慣性モーメントIが大きい方が、発生する角加速度αが小さくなります。
ある剛体の慣性モーメントの値は、その剛体の重心(=剛体が回転運動をする際の回転中心)から、どれだけ離れた位置に、どれだけ大きな質量が分布しているのかという二つの要素によって決定されます。つまり、図1のように、総質量が同じ二つの剛体であっても、重心から遠い部分の質量が大きい方が、慣性モーメントは大きくなります。
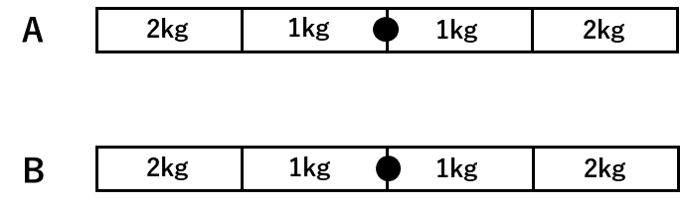
ここで一つ、物体が回転することに対する抵抗の大きさの決定に、質量が重心(回転中心)からどの程度離れた位置に存在しているのかが関係するということを実感できる方法を紹介しておきます。図2のように、ペンや箸などの細長い物体の片方の端を手で握った状態で、中身の入ったペットボトルや缶などの手ごろな重量の物体を押してみてください。このとき、手で握っているのと反対側の端の近くにペットボトルや缶を置いた場合の方が、手の近くの位置に置いた場合よりもずっと重たく(回転させづらく)感じるはずです。

前節でセグメント質量の推定方法についてお話しした際に既に少し言及しましたが、実際の動作解析研究の場面では、セグメントの慣性モーメントについても、いちいち厳密な方法で測るということはせず、人の部位ごとの慣性モーメントについて詳しく検討している論文に記載されている内容に基づき大まかな推定値を求めるということをしています。
4. 並進力と回転トルクを発生源ごとに分けて考える
二次元平面上における一つの剛体の瞬間における「力と加速度」および「トルクと角加速度」の関係性について表現した式として、以下のような三本の方程式を立てることができるというところまでお話ししました。
F_x=ma_x
F_y=ma_y
N=Iα
この式においてFやNが表しているのは、ある一つの剛体セグメントに作用している並進力や回転トルクをすべて一まとめに足し合わせた合計値です。次にしたいことは、この力やトルクを発生源ごとに分けて把握するということです。
前回同様に、下腿セグメントを例として考えていくことにしましょう。図3は人間の片側の下肢を単純化して表現したものです。図に示されているように、下腿セグメントは両端の一点において大腿セグメントおよび足部セグメントと連結しているものとします。前回もお話ししましたが、実際の人間の身体では、膝も足首もなかなかに複雑な関節構造をしているわけですが、現状のバイオメカニクス的動作解析研究においては、膝関節および足関節は、それぞれ大腿セグメントと下腿セグメント、下腿セグメントと足部セグメントが一点で連結したものと単純化してとらえるということを、多くの場合はしています。

まずは、並進力を発生源ごとに分けて考えてみましょう。下腿セグメント重心を上下左右に加速させる並進力の発生源として、膝関節において作用する大腿セグメントによって押されたり引っ張られたりすることによる力、足関節において作用する足部セグメントによって押されたり引っ張られたりすることによる力をまずは考えることができます。これら関節中心を作用点とする力のことをまとめて関節力(Joint force)と呼んだりします。
セグメントの上端および下端において作用する関節力に加えて、忘れてはいけないものとして、重力があります。重力は、セグメントを構成している小部分ごとに作用しているわけですが、その一つ一つを分けて考えるのは大変です。そこで、重心に下腿セグメントの質量全部が存在しており、それに対して重力が作用していると考えることが可能です(前回も言及しましたが、そのように考えても計算上問題が発生しない位置のことを重心と定義しているとも言えます)。
※さらに、実際には空気抵抗によってセグメントに力が作用していることもあり、とくに動作が高速な場合は無視すべきでない場合もあると思いますが、今回は空気抵抗による力の作用は存在しない(ゼロとみなしても計算結果に大きな影響を及ぼさない)ケースについて考えるという想定で話を進めることにします。
関節力については、水平方向の成分と上下方向の成分に分解して考えます。重力については、平らな地面上で運動している場合には、重力が作用する方向とY軸の向きが一致するので、水平方向に作用する力はゼロになります。また、重力の大きさは、セグメントの総質量mと重力加速度gの積によって定まります。重力加速度gとは、地球の重力の影響で物体にどのような落下加速度が生じるのかを表現した量であり、-9.8m/s2という定数になります。※厳密には、重力加速度gの値は、地球が完全な球形ではなく僅かに潰れた形状をしているために緯度によって僅かに変化するのですが、身体運動を分析する上では、この点についてはあまり細かく気にする必要はありません。
以上を踏まえて、並進運動についての二つの運動方程式を図4、5のように書き直すことができます。


回転運動についての運動方程式も同様に、図6のようにトルクを発生源ごとに分けた形に書き直すことができます。トルクの発生源の分け方は、力の分け方よりも少し込み入っていて、「関節力によるトルク」と「関節トルク」の二種類が出てきます。次節以降において、これらが意味している内容について、もう少し詳しく紹介していきます。

5. 並進力によって回転作用が発生する仕組み
まずは、「関節力によるトルク」とは何かということから紹介していきます。関節力によるトルクとは、関節力が並進作用と同時に発生させる回転作用のことです。こう言われてみても、ただちには納得できない人もいるかもしれません。剛体に作用する並進力が回転作用をも発生させるということについては、机に置いた鉛筆やペンを指で押して回転させてみることで、直観的イメージを得ることができるのではないかと思います。
図7のように、鉛筆の片側の端を鉛筆の長軸と垂直の方向に押してみると(=並進力を作用させてみると)、鉛筆の重心位置が移動するとともに、回転も(姿勢角も変化)します。このように、並進力が剛体に作用した場合、剛体には並進作用とともに回転作用も生じる場合があります。関節力(並進力)によってセグメントを回転させる作用(つまりトルク)が発生するのも、これと同じ原理によります。

ただし、剛体に作用する並進力はどんな場合でも回転トルクを発生させるわけでありません。並進力が回転トルクを発生させるか否か、あるいはどの程度の大きさの回転トルクを発生させるかということは、①力の作用点②力の方向③力の大きさ、という三つの要素に左右されます。
まず①力の作用点についてですが、図8のように鉛筆の中心(重心)付近を押してみても、鉛筆は回転せずに単に並進します。このように、並進力の作用点が重心と一致している場合は、並進力による回転作用(トルク)は発生しません。また、他の条件(力の方向と力の大きさ)が同じならば、作用点と重心との距離が大きくなるほどより大きなトルクが発生します。

次に②力の方向について見ていきましょう。図9のように今度は鉛筆の端を鉛筆の長軸方向に押してみます。重心位置と力の作用点に距離があるという条件を満たしているにもかかわらず、この場合も、鉛筆は回転せずに並進のみをします。このように、力の作用点が重心から離れた位置だとしても、力の向きが重心と力の作用点を結んだ直線と一致している場合もトルクは発生しません。また、他の条件(力の作用点と力の大きさ)が同じ場合に最も大きなトルクが発生するのは、重心と力の作用点を結んだ直線と垂直な方向に力が作用する場合になります。

最後に図10のように、③力の大きさについても考えてみましょう。鉛筆の端を長軸と垂直の方向に押すというよりは指ではじくようにしてみましょう。このとき、弱めの力ではじいた場合は、鉛筆は少ししか回転しませんし、強い力ではじけば大きく回転します。このように、他の条件(力の作用点と力の方向)が同じ場合は、力の大きさが大きいほど、発生するトルクも大きくなります。

前節の終わりにおいて示した、トルクを発生源ごとに分けて書き直した回転運動についての運動方程式の中の「関節力によるトルク」に対応する項は、r/F/sinθという三つの要素によって構成されていました。実は図11のように、これら三つの記号によって、並進力の回転トルクへの変換の有無や程度を決定する三つの要素が表現されているのです。

まずr(rankle、rknee)は、セグメント重心と関節力が作用しているセグメント端点までの距離(要素1)を意味しています。前回、セグメント端点(=隣接セグメントとの連結ポイント=関節中心)の位置を算出しておくということについて一節を割いて紹介しました。この情報が運動方程式中で必要になるのは、このrの値を決定するために使われるからなのです。
次に、F(Fankle、Fknee)は力の大きさ(要素3)を意味しています。この力Fは、力の作用点から重心方向に向かう方向の成分と、それと垂直な方向の成分に分解することができます。このうち前者は上で紹介したように、回転作用を発生しません。つまり、関節力のうち後者の成分のみが回転作用を発生することになります。
そして、力Fにsinθ(sinθ1、sinθ2)を掛けた値は、この垂直方向の成分の大きさと一致します。つまり、関節力のトルクを表現した式にsinθという要素が含まれているのは、力Fのうち、回転作用を発生させる成分のみを取り出すためということになります(要素2)。
6. 並進力である筋張力が回転作用に変換される仕組み
次に、回転運動についての運動方程式に含まれているもう一つの要素である、関節トルクとは何かということについて考えていきたいと思います。「関節トルクとは何か?」という問いに対する私なりの回答は、「関節トルクとは、その関節をまたいで付着している筋が力を発揮することによって発生する、関節を構成する二つのセグメントを回転させる『第一次的な』力学的作用のことである」というものです。したがって、例えば股関節トルクとは、「股関節をまたいで付着する筋によって発揮された力によって発生する、骨盤セグメントと大腿セグメントを回転させる第一次的な力学的作用」を意味するということになります。
「第一次的な」と括弧でくくって強調したのは、この部分が私なりの整理の肝となる部分だからです。以下では、筋が力を発揮することによって発生する力学的作用を、
①第一次的な並進作用(力)
②第一次的な回転作用(トルク)
③第二次的な並進作用(力)
④第二次的な回転作用(トルク)
の四つに分けて整理するということを試みたいと思います。
まず、①第一次的な並進作用についてですが、これは二つの並進力が相殺し合うことによってゼロになります。これは、ちょっとしたマジックのような仕組みによって起こります。筋が力を発揮する(収縮する)ことによって発生する出来事としてまず挙げられるのは、図12のように骨(セグメント)との付着部において骨を引っ張るような力(並進力)が発生するということです。
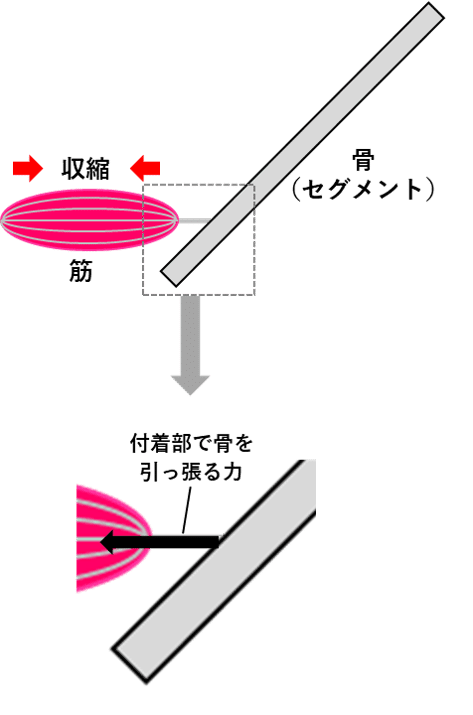
仮にこの力しかセグメント(骨)に作用していないのならば、引っ張られた方向に加速度が発生することになります。しかしここで図13のように、関節において隣のセグメントに押し返されることによって、大きさが同じで向きが正反対の力が発生します。これによって、二つの力を足し合わせた場合の力の大きさはゼロになります。これが、「第一次的な並進作用がゼロになる」基本的原理です。

この二つの並進力による並進加速度を発生させる「効果」は相互に打ち消されてしまうわけですが、力自体が作用しなくなったわけではありません。そして、この二つの並進力が存在することでそれぞれ回転作用が発生し、しかもそれらは並進加速度とは異なり部分的にしか打ち消し合いません。なぜなら、二つの並進力の作用点が異なることによって、セグメント重心から作用点までの距離が二つの力では異なっているからです。
図14に示したように、二つの力のセグメント長軸と垂直方向の成分は、大きさが等しく向きが反対になります。この力の大きさを仮に5としましょう。また、セグメント重心から関節中心までの距離を10、セグメント重心から筋の付着位置までの距離を8としましょう。そうすると、関節中心において作用している並進力によって発生するトルクの大きさは10×5=50であり、筋の付着部において作用している並進力によって発生するトルクの大きさは8×5=40ということになります。
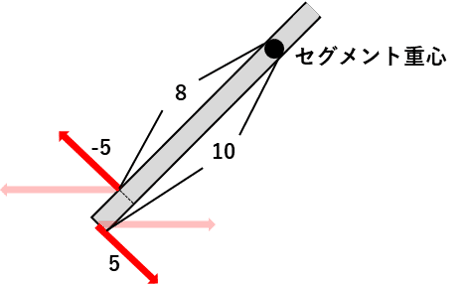
この二つのトルクはセグメントを回転させる向きが、前者は左回転(反時計回り)、後者は右回転(時計回り)と異なります。セグメントを左回転させる50という大きさのトルクのうち、40までは右回転させるトルクと打ち消し合います。したがって、これら二つの並進力によるトルクを合算した値は、左回りを正とする場合、+10という値を持つことになります。
私が、「筋が力を発揮したことによって発生する第一次的な回転作用」という言葉で意味しているのは、この二つの並進力によるトルクを足し合わせたトルク(二つのトルクの回転効果のうち、相殺されきらない部分)のことです。そして、関節トルクとは、この「第一次的な回転作用」のことを意味しています。
ここまでの内容を読まれた方の中には、筋が力を発揮しても、その筋がまたいでいる関節に発生する関節力の大きさには影響しない(第一次的な並進作用は相殺されてゼロになるのだから)と考えてしまうかもしれませんが、実はそうではありません。
図15のように棒の左端点が土台と一点で連結している(これは身体でいうところの関節に相当するものと考えてください)という状況について考えてみましょう。
※なお、ここでは棒に作用する重力は存在しないものと仮定して話を進めます。
この棒は左端点がこの位置から動かせないという拘束条件がある以外は自由に動くことができます。また、筋と同じように、収縮することによって力を発揮する機構が、連結点をまたぐようにして、棒と土台にそれぞれ付着しています。そして、この筋が力を発揮すると棒は、連結点を中心にして弧を描くように動くと考えられます。

もし仮に、ここまで考察してきた作用しか発生していないとするならば、この筋が力を発揮したことによって発生する並進作用はゼロになり、回転作用のみが発生していることになります。したがって、もしこれらの力・トルクのみしかこの棒に対して作用していないのであれば、棒の重心位置は動かず(並進加速度は発生せず)、重心を中心とした回転運動のみが生じなければなりません。
しかし、棒が土台との連結点を中心にして弧を描くように動く場合、図16のように棒の重心位置は変化することになります。つまり、このままでは、棒を並進させる力(を合算した値)はゼロであるにもかかわらず、棒が並進運動をした(棒の重心に並進加速度が発生した)ということになってしまい、力学法則との間に矛盾が生じてしまいます。

この矛盾は、筋が力を発揮することによって発生する力学的作用は実は他にもあるため、解消することができます。仮に棒が重心を中心に回転するならば、棒の左端点は土台との連結ポイントから離れてしまうことになります。このとき、連結ポイントから離れようとする棒の左端点を、その位置から離さないように束縛する力が、土台から棒の左端点に作用することになります。今回のケースでは、棒の左端点は土台を押すように動こうとするのですが、それに抵抗して土台から押し返されるような力を受けることになります。このような並進力が発生しているので、棒の重心位置が並進運動をしたとしても力学的に矛盾はないのです。
実際は、第一次的な回転作用とこの作用は同時に発生するのですが、人間的に納得しやすい解釈として、第一次的(直接的)には重心を中心として棒を回転させるような作用が発生し、それによって生じるはずの加速度がセグメントの拘束条件を破綻させそうになる場合には、それを防ぐような力が二次的(間接的)な作用として発生するというふうに理解しておくと分かりやすいと思います。そこで、この作用のことを、第二次的な並進作用と呼ぶことができるでしょう。
そして、もう既にお気づきの方もいるかもしれませんが、この第二次的な並進作用の作用点は、重心から離れた位置なので、図17のように、「第二次的に発生する並進力によるトルク」というものも発生します。このトルクのことを第二次的に発生する回転作用と呼ぶことができるでしょう。

本節冒頭で述べた内容の確認になりますが、関節トルクとは、筋が力を発揮することによって発生する可能性のある四つの作用のうち、②第一次的に発生する回転作用のことを指しています。そして、①第一次的に発生する並進作用の合計値はゼロになります。また、③第二次的に発生する並進作用については、関節力の中に含まれ、④第二次的に発生する回転作用については、関節力によるトルクの中に含まれているということになります。以上をまとめると図18のようになります。

7. 関節トルクは複数の筋の力発揮によって生じる第一次的な回転作用を合算したものである
関節トルクというのは、その関節をまたいで付着している筋が発揮した力によって生じる、筋が付着しているセグメントに対して働く第一次的な回転作用のことだと述べました。前節では、原理的な説明をするために、ただ一つの筋が力を発揮した場合に生じる力学的作用について考えました。しかし、実際には、一つの関節をまたいで付着している筋は複数存在しています。
ここで注意しておく必要があることは、9節において紹介する手続きを通じて算出される関節トルクの値とは、ある関節をまたぐすべての筋が個別に発揮した力によって生じる、個別の筋ごとの第一次的な回転作用をすべて足し合わせたものだということです。したがって、例えば、ある関節まわりに筋A、筋Bという二つの筋が付着しており、筋Aが+20、筋Bが(筋Aとは反対向きにセグメントを回転させる)-10という第一次的な回転作用を発生させているという場合には、算出される関節トルクの値は、+10ということになります。
個別の筋ごとに発揮された力によって発生する第一次的な回転作用のことを、関節トルクとは区別して「筋トルク」と呼ぶこともあります。個別の筋ごとに発揮された筋トルクの値を推定するためには、今回紹介しているのとは異なる研究手法を用いる必要があります。
※なお、筋トルクの推定は、関節トルクの推定と比較すると、推定値の正しさに疑問が残る部分が多いとされています。
8. 大きさが等しく向きが反対のトルクが発生する仕組み
もう一つ紹介しておく必要がある事柄として、ある一つの筋が力を発揮すると、その筋が付着する二つのセグメントに対して、大きさが同じで回転の向きが反対のトルク(第一次的な回転作用)が発生するということです。したがって、複数の筋が発揮した力によってそれぞれ生じる第一次的な回転作用を足し合わせたものである関節トルクについても、同じく大きさが同じで向きが反対の関節トルクが作用するということになります。この知識を活用することが、次節において紹介する、関節トルクの値を算出する作業の際にとても重要になります。
二つのセグメントに作用する関節トルクの回転方向が反対になるという点については、大きな問題はなさそうですが、発生するトルクの大きさまでが常にまったく同じになるという点については、必ずしも自明なこととは思えない人が多いのではないかと思います。そこで本節の以下では、細かな数学的な話は脇において、二つのセグメントに発生する関節トルクの大きさが同じになることについての定性的な説明を与えてみたいと思います。
ある筋が力を発揮した時に発生する関節トルク(第一次的な回転作用)の大きさは、「関節中心と筋の付着部までの距離」と「筋が発揮した力のうちセグメント長軸と垂直な成分」を掛け算した値となります。「関節中心と筋の付着部までの距離」というのはここで初めて出てきたものです。これが重要な意味を持つのは、図19のように、関節トルクの大きさとは、セグメント重心から、この距離と同じだけ関節中心の方に向かう位置を作用点として、筋が発揮したのと大きさが同じで向きが反対の力が作用した際に生じるトルクの大きさと一致するからです。
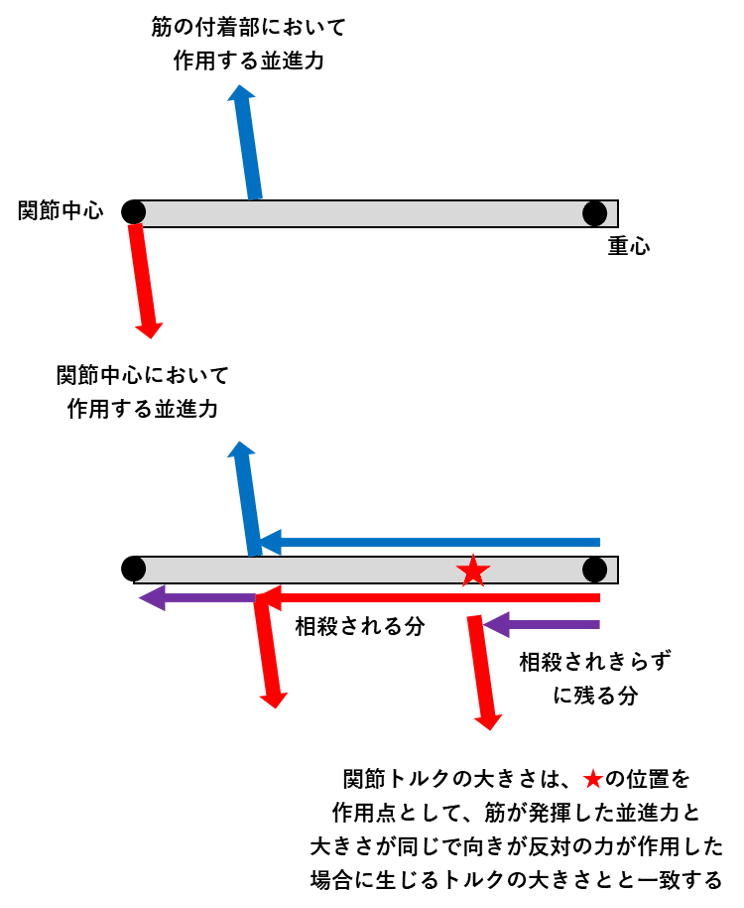
「関節中心と筋の付着部までの距離」と「筋が発揮した力のうちセグメント長軸と垂直な成分」の双方の値が二つのセグメントで同じ場合は、当然のことながら、二つのセグメントに発生する関節トルクの大きさは同じになります。こうなるのは、図20のように、関節中心から筋の付着部までの距離が二つのセグメントで同じになる場合です。

話がややこしくなってくるのは、筋の両端の、関節中心からの距離が異なるという場合です。例えば、セグメント1との付着部よりもセグメント2との付着部の方が関節中心からの距離が大きいというケースについて考えてみましょう。この場合、関節トルクの大きさを規定する二つの要素のうちの一つである、関節中心から筋の付着部までの距離はセグメント2の方が大きいのだから、発生する関節トルクの大きさが同じになるためには、力のセグメント長軸に対する垂直成分については、セグメント1の方が大きくなる必要があります。
ここで、筋のセグメント2との付着部を以下の2通りに変化させてみた場合について考えてみましょう。
①セグメント1よりも関節中心から遠い位置に付着している場合
②セグメント1よりも関節中心に近い位置に付着している場合
図21のように、①セグメント1よりも関節中心から筋の付着部までの距離が長くなることで、筋が発揮する力の作用線はセグメント2の長軸と平行に近くなっていきます。つまり、筋が発揮する力のセグメント2の長軸と垂直な成分の比率は小さくなっていきます。また、このとき力の作用線はセグメント1の長軸との関係では垂直に近くなっており、したがって、筋が発揮する力のセグメント1の長軸と垂直な成分の比率は大きくなります。
反対に、②セグメント1よりも関節中心から筋の付着部までの距離が短くなることで、筋が発揮する力の作用線はセグメント2の長軸と垂直に近くなっていきます。そして、やはりこのとき、力の作用線とセグメント1の長軸との関係は平行に近くなっていきます。

このように、発生する関節トルクの大きさを規定する二つの要素のうちの片方が相対的に大きくなると、もう片方が相対的に小さくなることで、結果的に二つのセグメントに対して同じ大きさ(で向きが反対)のトルクが発生することになるのです。
9. 末端から順繰りに関節力と関節トルクを算出していく
4節では、下腿セグメントを例として、力とトルクをその発生源ごとに分けて表現した運動方程式を立てるというところまでお話ししました。しかし、このままだと下腿セグメントに作用している具体的な力やトルクの値は分かっていないので、具体的な値を知りたいところです。
ここで問題となるのが、立てられた方程式の数に対して、未知数が多すぎるということです。一つのセグメントについて立てられた運動方程式は計3本であるのに対して、以下でお話しするように未知数は6つもあります。
基本的にすべての未知数の値を特定できるためには、値を特定したい変数の数と同じだけの方程式を立てられている必要があります。例えば、y=2xという式だけでは、yの値もxの値も一つに絞り込むことはできません。ここにもう一つ、y=3x+2という式があれば、二つの方程式を連立することで、x=-2、y=-4というように値を一つに絞り込むことができます。
あるいは、別の発想として、未知数の数を立てられている方程式の数の分まで減らすことができれば、そうすることによっても、方程式を使って残りの未知数の値を特定することが可能になります。例えば、y=2xという一本の方程式しか立てられていなくても、x=3であるということを特定する(=未知数を2つから1つに減らす)ことができれば、y=6であるということを導くことができます。本節において紹介するのは、後者の発想に基づいて、末端部から順々に身体に作用している力およびトルクを推定していくという手法です。
下腿セグメントに作用している力やトルクを算出するには、その前段階として足部セグメントに作用している力やトルクを算出する必要があります。そして、足部セグメントに作用している力やトルクを算出する手順については、足部セグメントが地面から離れている場合と、地面に接地している場合に分けて紹介する必要があります。
図22のように、足部セグメントが地面から離れている場合、足部セグメントに対して作用する力・トルクの発生源は、足関節において作用している関節力と足関節をまたぐように付着している筋群によって発生する関節トルクのみです。この場合、未知数は三つだけなので、三本の運動方程式によって、それぞれの値を決定することができます
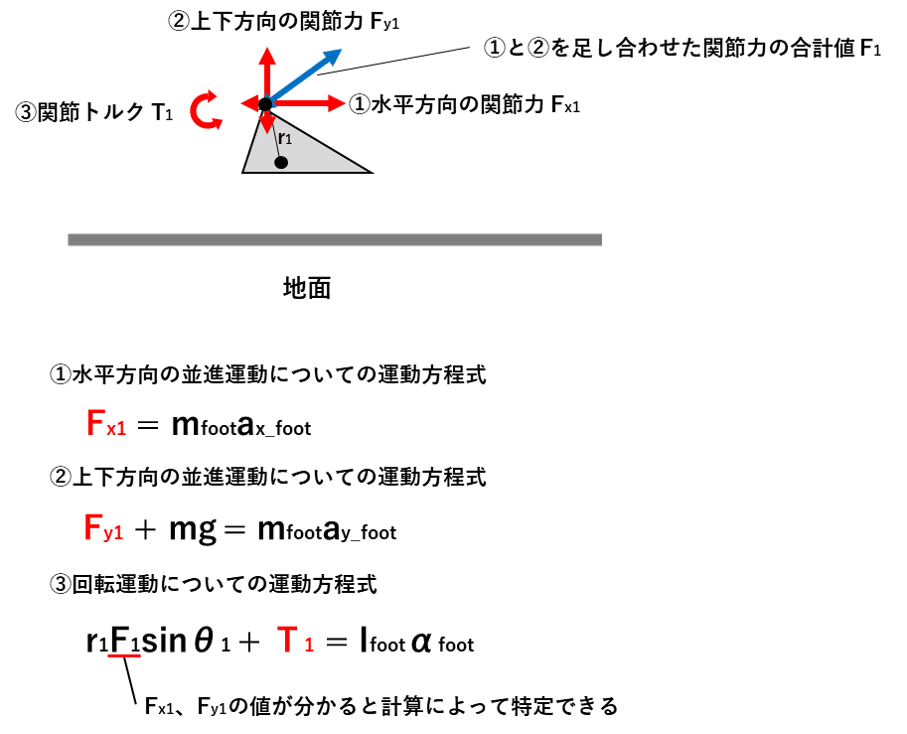
足部セグメントが地面に接地している場合には、地面からの反発力(地面反力)が足圧中心に作用することになります。したがってこの場合は、未知数の数が方程式の数を上回ってしまいます。ここでフォースプレート(地面反力計)という計測機器が活躍します。フォースプレートを用いることで、足部セグメントに作用する地面反力のX軸方向、Y軸方向それぞれについての大きさと、足圧中心(実際は足裏全体に作用している地面反力を一つの作用点に集約して計算する際に、作用点とみなすべき場所)がどこかを計測することができます。

地面反力をフォースプレートで直接計測してしまうことで、図24のように、連立方程式中の未知数を三つに減らすことができ、足関節において作用する関節力および関節トルクの値を特定することが可能になります。なお、三つの式から足関節において作用する関節力および関節トルクを特定する順序としては、以下のようになります。
①水平方向と上下方向の関節力を算出する
②関節力が分かったことで、関節力によるトルクの値が分かる
③関節力によるトルクの値が分かったことで、関節トルクの値を特定することができる

足部セグメントの場合は、地面から離れていることで足裏に作用する力をゼロとみなして良かったり、フォースプレートによる直接計測によって未知数を減らすということが可能でした。次に下腿セグメントに作用している力およびトルクを特定したいわけですが、下腿セグメントの場合は、図25のように、両端に作用する関節力、足関節トルクと膝関節トルクの計6つの未知数が存在しますし、足裏の場合と違って、足関節において下腿セグメントに作用する力を直接計測するということもそう簡単にはできそうにありません。

ここで役に立つのが、前節で紹介した「筋が付着する二つのセグメントに対しては、大きさが同じで向きが反対の関節トルクが作用する」という知識です。この知識を前提にすることで、足部セグメントについて計算を行った際に特定できている、足部セグメントに作用する足関節トルクの値の符号を反対にするだけで、下腿セグメントに作用する足関節トルクの値を決定できます。
また、関節力についても、物体Aが物体Bに力を作用させた場合、物体Bから同じ大きさの反対向きの力を受けることになるという「作用反作用の法則」を利用することで、その値を特定することができます。つまり、足関節において足部セグメントに対して作用していた関節力と大きさが同じで向きが正反対の力が下腿セグメントに作用すると考えれば良いということです。
このように考えることによって、図26のように、未知数は膝関節において作用する関節力と関節トルクのみとなるので、足部セグメントにおいて足関節において作用する関節力と関節トルクを特定したのと同様の手順によって、これらの値を特定することができます。まったく同じ作業を大腿セグメントに対しても実行することによって、股関節に作用する関節力とトルクも算出することができます。さらに、同じことを反対側の足部セグメント、両側の手セグメント、頭部を起点にして実行することで、全身の主だった関節に作用している関節力と関節トルクを推定することができます。

10. おわりに
この関節トルクを算出するというところまでが、バイオメカニクス的動作解析研究においてよく整備されている標準的(基本的)研究手法と言えます。これによって、ある動作を実行している時に、全身の筋がどのように力を発揮しているのかということを、(あくまでも関節ごとにまとめた大まかな形ではありますが)把握することが可能になります。
次回は、力やトルクの、加速度や各加速度への貢献を比較するというアイデアについて紹介した上で、今回紹介した逆動力学的アプローチによる手法だと、このアイデアを完遂する上で、あるところで行き詰まりが生じてしまうということを指摘したいと思います。さらに、この行き詰まりを解消してくれるかもしれないアプローチとして、ここ20年間くらいの間、バイオメカニクス的動作解析研究の領域において注目を浴びてきた研究手法について、その概略を紹介してみたいと思います。
次回
この記事が気に入ったらサポートをしてみませんか?
