世界一わかりにくい算数(小学校4年_データと図形)
1.日本のカリキュラム
日本のカリキュラムは整理すると次のようになります。
(以下のサイトを参考にしています。)
内容を私なりにまとめると以下のようになります。
(B.図形)
・直線の平行や垂直、対角線
・平行四辺形、ひし形、台形
・立方体や直方体について辺や面の垂直と平行、見取り図と展開図
・平面図形の面積(cm ,m ,km ,a ,ha)
・角度を測る
(C.変化と関係)
・変化の様子を表、式、折れ線グラフで表したり、読み取ったりする
・簡単な割合
(D.データの活用)
・2つの観点(日時と場所等)から表データを作成する。
2.米国のカリキュラム
世界大学ランキングで上位を占める大学が多い米国を参考にします。
ソースはカーンアカデミーを参考にしています。
3rd grade 、4th grade、6th gradeを参考にしています。
3rd grade
・ 面積や外周
4th grade
・ 平面図形「三角形、垂直、平行」と角度
・ 長さ、外周、面積の関係
・ 角度の測定
6th grade
・ 3次元図形
データの活用については、米国ではラインプロット位であまり複雑な表はやらないようです。
正直、高校になってからや、社会人になってから「Quality Control:QC」等でさらっと見るだけで習得できるものを、小学生の間に頑張って教えるより、習得が難しく大切な小数や分数にもっと時間を使ったほうがいいと個人的には思います。
また「大人になったらデータを活用する場面があるから、データ活用を学校で教えよう」とか、「コンピュータを使用する際にプログラミングが必要だから学校で教えよう」とか、そういった足し算の発想によってカリキュラムが増えていっているように感じます。
(逆に本当にAI時代に必要な分野(行列)はカットされていると思いますが。)
子供のころから学んでいると、「データを日々の生活に活用しようとする子供」になるという認識も違うのではないかと思います。それは自分がそのように学んでいれば、変わったはずという大人の認識のゆがみではないかと思います。
自分の子供は自分と同じようなことを時代の変化に合わせてやるだけです。
教育への過度な期待をもう少し緩和する必要があると考えています。
私はこれらの考えから教育内容をより高等な学問を理解できるだけの最小限に留めて、その代わり習得状況に併せて早く学習段階を進めるような教育カリキュラムに変える方がよいのではと個人的には考えています。
3.理解と社会的実践
(1)角の大きさの測定
辺と辺の開き具合を角と呼び、線分ABとBCがあるときにできる角を角ABCと表現し、記号で∠ABCと書きます。
角の大きさは角度(数値°)で表され、測定する道具が分度器です。
この角度ですが、以下の図のように赤と青の2通り考えられると思います。

角度の小さい角(赤)と角度の大きい角(青)がありますが、∠ABCは特にことわりがなければ、通常角度の小さい角(赤)を指します。
次にいろいろな角度を見ていきたいと思います。赤線の角に注目します。

直角が90°となり、それより小さい角を鋭角といいます。
真っ直ぐになった場合180°となりますが、90°から180の間の角を鈍角と言います。
180°から90°増えた角は270°となり、さらに90°増えると一周し360°となります。
分度器を使っていろいろな角度を測って角度の感覚を身に着けていくのがよいと思います。
[算数の問題]
(問)
AとBの赤線で描いた角度を計算してください。またAの角を何というか答えてください。
(分かりづらいと思いますが、Bの問題の120°は、青線の全部の角度となっています。)

(答え)
A:1周は360°です。そのため 角A+310=360 となります。
したがって A=360-310=50 となり、角Aは50°となります。
さらに角Aは90°より小さいので鋭角といいます。
B:全体で120°に注目します。角B+20+30=120 となります。
したがって B=120-50=70 となり、角Bは70°となります。
(2)垂直と平行と四角形
〇 平面と空間
直線の関係性を確認するまえに、平面について確認します。
まず重ならない2点を考えます。そうするとどのような2点でも直線を引くことができます。
次に重ならない3点を考えます。この3点は2つの関係性がありえます。
① 2点で直線が引けるので、3点目が同じ直線上にある場合を考えることができます。
② 2点で直線が引けるので、3点目に同じ直線上にない点をとると3角形ができます。この三角形は紙に書くことができますが、この紙を無限に広げたようなものが平面となります。

ちなみに重ならない4点は、同じ直線上にある場合、同じ平面にある場合、同じ平面にない場合があります。

〇 同じ平面にある直線の関係
これから同じ平面にある直線の関係を見ていきたいと思います。
2つの直線があるとき、交わる場合と交わらない場合があります。
交わる場合の中で、直角で交わったとき、垂直といいます。
交わらない場合、2つの直線の関係を平行といいます。

〇 平行四辺形
平行な辺がある四角形についてみてみたいと思います。

台形は1組の向かい合う辺(つながってない辺どうし)が平行な四角形です(辺アと辺イ)。
平行四辺形は2組の向かい合う辺が平行な四角形です(辺アと辺ウ、
辺イと辺ウ)。
平行四辺形はいくつか性質があります。なぜそんな性質があるかということは中学生の図形を学ぶことで示すことができますが、現時点ではこんな性質があるんだなと知っておいてもらえればと思います。
性質1)2組の向かい合う辺の長さが等しい
<辺アの長さ=辺ウの長さ、辺イの長さ=辺ウの長さ>
性質2)2組の向かい合う角度が等しい
<角アの大きさ=角ウの大きさ、角イの大きさ=角ウの大きさ>
平行四辺形の性質1のさらに特別なケースとして、「全ての辺の長さが等しい」平行四辺形を考えてみます。それはひし形になります。
平行四辺形の性質2のさらに特別なケースとして、「全ての角の大きさが等しい」平行四辺形を考えてみます。全ての角が90°(直角)となります。
それは長方形になります。
そして「全ての辺の長さが等しい」、さらに「全ての角の大きさが等しい」平行四辺形を考えます。それは正方形になります。
つまり正方形、長方形、ひし形は平行四辺形の特別なケースと考えることができます。
〇 対角線と平行四辺形
ある図形について隣り合わない点同士を結んだ線を対角線と言います。
(三角形ではすべての点が隣り合うので、三角形では対角線はありません。)
四角形では下の図のように2つの青い線が対角線となります。

この対角線の利用場面として、平行四辺形、ひし形、長方形、正方形を描きたいときに便利です。それぞれ対角線に特徴があるためですが、この特徴がなぜ成り立つかは中学で図形を学んで始めて理解できます。
ここでは対角線の特徴があることを知ることで、平行四辺形、ひし形、長方形、正方形を上手く描くことができるという程度の認識でいいと思います。

① 平行四辺形:2線交わらせて、交わった点から線ごとに同じ長さのところに点を取り、この4点を結ぶと平行四辺形になります。
つまり平行四辺形の対角線は、「それぞれの真ん中の点で交わる」という性質があります。
② ひし形:2線を垂直に交わらせて、交わった点から線ごとに同じ長さのところに点を取り、この4点を結ぶとひし形になります。
つまりひし形の対角線は、「それぞれの真ん中の点で交わり」、さらに「対角線が垂直である」という性質があります。
➂ 長方形:2線交わらせて、交わった点から同じ長さのところに点を取り、この4点を結ぶと長方形になります。
つまり長方形の対角線は、「それぞれの真ん中の点で交わり」、さらに「対角線の長さが同じ」という性質があります。
④ 正方形:2線を垂直に交わらせて、交わった点から同じ長さのところに点を取り、この4点を結ぶと正方形になります。
つまり正方形の対角線は、「それぞれの真ん中の点で交わり」、さらに「対角線が垂直である」、さらに「対角線の長さが同じ」という性質があります。
このあたりの分野は勉強というよりはいろいろな図形を定規、分度器、コンパスを使って描いてみたり、図形の長さや角度を測るという経験を積むことが大切だと思います。
また説明はしましたが、平行四辺形、長方形、ひし形、正方形の対角線をこの段階でここまで細かく教える意味もそこまでないのではないかとも感じます。
中学生で図形を学ぶ際に教える方向性のほうが良いのではと感じました。
それよりも「長方形は平行四辺形である」という問題に対して、
「平行四辺形は2組の向かい合う辺が平行な四角形」のことで長方形も2組の向かい合う辺が平行な四角形だから、この問題の答えは「Yes」だと考えられる論理力を鍛える方がよいのではないかと思いました。
[算数の問題]
(問1)
以下にある図形は平行四辺形と直角三角形です。どの辺とどの辺が平行、または垂直の関係にあるか答えてください。

(問2)
以下の図のように4点とり、四角形を作ったとき、図形A,B,Cは「平行四辺形、長方形、ひし形、正方形、どれでもない四角形」のどれになるか答えてください。(赤く示した部分は90°です。)

(答え)
(問1)
平行四辺形には、辺を伸ばして直線にしても交わらない辺があります。
辺Aと辺Cはどこまで伸ばしても交わらないので、平行の関係にあります。
辺Bと辺Bはどこまで伸ばしても交わらないので、平行の関係にあります。
直角で交わる辺はないので、垂直の関係はありません。
直角三角形は、すべての辺が交わっているので、平行の関係はありません。
辺Eと辺Fは直角に交わっているので、垂直の関係にあります。
(問2)
この交わっている線は対角線となっています。
図形A: 対角線がそれぞれの真ん中の点で交わっています。つまり4点とり、四角形を作ったとき「平行四辺形」になります。
図形B: 対角線が垂直の関係にありますが、それぞれの真ん中の点で交わっていません。そのため「どれでもない四角形」となります。
図形C: 対角線がそれぞれの真ん中の点で交わっていて、さらに対角線の長さが等しいです。そのため図形Cは「長方形」になります。
(3)面積
〇 面積の基本的な考え方と単位
面積とは図形の広さや大きさのことをいいます。面積を比べるためには測って、数字にして比べたいという発想になります。下の図形を見てください。

薄い線で方眼紙や原稿用紙のような線が入っていますが、この1マスが何個あるか数えることでどちらが広いか、または同じか比べることができます。
このマスの数が面積となります。
これから面積を求めるための公式のようなものが出てきますが、基本はこのマスの数を数えるという点にあります。
面積の単位は1マスの縦と横がどれくらいの長さかによって決まります。
例えば縦と横が1cmの時、1マスの面積は1$${cm^2}$$と表されます。そしてこのマスが5個あれば面積は5$${cm^2}$$といいます。
この肩に乗っている小さい数字の2は、1cm×1cmとしてcmが2回かけられていることを表すもので累乗(るいじょう)と呼ばれ、2の場合は2乗といいます。
また2乗のことを平方といい、$${cm^2}$$を平方センチメートルといいます。
他にも体積というものを表す単位で1$${cm^3}$$というものがあるのですが、これは1cm×1cm×1cmとしてcmが3回かけられていることを表します。
この場合は3乗となり、立方というので、$${cm^3}$$を立方センチメートルといいます。
(数学的には〇乗といい、単位などでは平方や立方が使われると思ってください。)
それでは代表的な長方形や正方形の面積を考えてみます。

長方形の面積を求めるために、1cm×1cmのマスがいくつ入るか計算する場合、横の長さだけ横方向にマスがあり、さらに縦の長さだけ縦方向にマスがあることを考えるとかけ算でマスの数が求められます。
(横の長さ)×(縦の長さ)=3×2=6 マス入るので、6$${cm^2}$$と計算できます。
正方形の面積も考え方は同じですが、縦も横も長さが等しくなります。そのため1辺×1辺で面積が求められ、2×2 =4 マス入るので、4$${cm^2}$$と計算できます。
これらは公式のように書かれることはありますが、考え方を理解してもらえればと思います。
最後に面積の単位換算について説明します。
1m×1mを1マスと考えると、面積の単位は1$${m^2}$$となり、平方メートルといいます。
これを$${cm^2}$$に変換するとどうなるか考えます。
1m=100cm です。そのため 1m×1m=100cm×100cm となり、
1$${m^2}$$=10000$${cm^2}$$ となります。
では1平方キロメートルを平方メートルと平方センチメートルで表します。
1km×1km=1,000m×1,000m=100,000cm×100,000cm となるので、
1$${km^2}$$=1,000,000$${m^2}$$=10,000,000,000$${cm^2}$$となります。
長さの単位を合わせたあと、面積なのでかけ算をします。そのため単位変更の影響が2回でてくる点に注意してください。
〇 特定の仕事で使われる面積の単位(a,ha)
面積は歴史的に土地との結びつきが強いです。そのため土地の面積を扱うような業種で使用する単位があります。
a(アール)やha(ヘクタアール)というのも代表的な例です。作付面積と言われる農業で使用する単位など比較的特定のケースで使用されます。
1a=10m×10m=100 $${m^2}$$、1ha=100m×100m=10,000$${m^2}$$です。
1辺の長さが10倍になると面積は100倍になります。
覚える必要がある場合は、何m×何mが1aまたは1haだったか覚えるのがよいとは思います。
小学生のとき何故か覚える必要がありましたが、私は問題にするときは、テスト用紙に単位換算を書いておき、適切に使えるか見ればよい程度の知識ではないかなと考えています。
〇 外周の長さとは
図形のすべての辺の長さを足したものを図形の外周と呼びます。
例えば花だんを作りたいときなどに、周囲をレンガ等で囲むことがありますが、その場合必要なレンガの数を考える場合、図形(花だんの形状)の外周を計算する必要があります。
外周を計算する場合、全ての辺の長さを測る必要がありますが、長方形や正方形はすべての辺の長さが分からなくても計算できます。

長方形は縦の長さと横の長さが一つづつわかれば計算できます。
縦の長さは2辺とも同じで、横の長さも2辺とも同じためです。
したがって図の長方形の外周は(2+3)×2=10 10cm と計算できます。
ちなみに2組の向かい合う辺の長さが等しい平行四辺形も同じ方法で計算できます。
正方形は一辺の長さが分かれば4倍で計算できます。
したがって図の正方形の外周は2×4=8 8cmと計算できます。
ちなみに4つの辺の長さが等しい四角形であるひし形も正方形と同じ方法で外周を計算することができます。
長さを測るということは、すごく大きなものや小さなものになればなるほど大変になります。
したがって測らないといけない辺は少ない方がよいので、その図形の特徴に注目し、測る辺の数を減らすことができないか考えるのもよいでしょう。
[算数の問題]
(問1)
どっちの面積が大きいでしょうか。

(問2)
56$${cm^2}$$の面積である長方形があります。縦の長さが7cmのとき、横の長さは何cmでしょうか。
(問3)
下の図の面積を求めてください。

(問4)
144$${cm^2}$$の面積である正方形があります。1辺の長さは何cmでしょうか。また外周は何cmでしょうか。
(問5)
外周が90cmの長方形があります。縦の長さが27cmのとき、横の長さは何cmでしょうか。また面積は何$${cm^2}$$になりますか。
(問6)
1辺が6cmの正三角形の外周は何cmでしょうか。
また以下の図形の外周が20mの時、?mを求めてください。

(答え)
(問1)
図形Aの面積:4×10=40 40$${cm^2}$$
図形Bの面積:6×8=48 48$${cm^2}$$
図形Bのほうが大きいことがわかります。
(問2)
長方形の面積=(縦の長さ)×(横の長さ)なので、7×(横の長さ)=56となります。(横の長さ)=56÷7=8 横の長さは8cmとなります。
(問3)
このような図形の面積の公式はありません。こういった場合は図形を分割することを考えます。そうすると7cm×4cmの長方形と4cm×9cmの長方形にわけて考えることができます。
したがって面積は、7×4+4×9=28+36=64 64$${cm^2}$$が答えとなります。
(問4)
正方形は一辺の長さが分かれば、面積を求めることができます。
正方形の面積=(一辺の長さ)×(一辺の長さ)で求めることができるので、1辺の長さを10cm位から試してみるとよいと思います。
10×10=100, 11×11=121, 12×12=144 となるので、一辺の長さは12cmです。
また外周は4倍すればよいので、4×12=48 48cmとなります。
(問5)
長方形の外周=2×(縦の長さ)+2×(横の長さ)となるので、
90=2×27+2×(横の長さ) となり、2×(横の長さ)=90-54=36
横の長さ=36÷2=18 18cmとなります。
面積=(縦の長さ)×(横の長さ)=27×18=486 よりこの長方形の面積は、486$${cm^2}$$となります。
(問6)
正方形は全ての辺の長さが等しい三角形です。そのため外周は6×3=18
18 cmとなります。
次に図形の外周は、6+4+1+1+5+?=20 となるので、17+?=20
?=20-17=3 ?mは3mとなります。
[社会実践問題]
あるマンションが坪単価約66万円、総面積坪数が30坪の時、いくら位で購入できるでしょうか。
坪というのは面積の単位で、坪単価とは1坪でいくらの値段になるか示したものです。
(答え)
坪単価約66万円ということで、1坪で66万円の値段になることが分かります。総面積は30坪なので、マンションの価格は坪単価×総面積で求めることができそうだと考えることができます。
660,000×30=19,800,000 より1980万円位だろうと考えることができます。
このように社会に出てからも、面積というものは関りがあることを知っておいても損はないと思います。
(4)直方体と立方体
〇 直方体と立方体
紙にかける図形は縦と横の長さを持つ図形で、ティッシュボックスのような高さを持った図形を表すことはできません。そのため点線等を使って空間上の図形を表現します。この空間の図形を立体図形といいます。
この立体図形の中で、正方形だけでできた箱を立方体、長方形でできた箱を直方体といいます。ちなみに正方形も長方形の特別なケースなので、直方体には正方形が含まれることもあります。

〇 面と辺の関係
垂直や平行について立体図形の場合を見ていきます。
まず面どうしの関係について平行な面や垂直な面を考えます。以下の図形はすべての頂点にアルファベットを振っています。
面ABDCといった場合、頂点A,B,C,Dで囲まれた面を表します。線分ABと言ったら、頂点ABをつないだ線を表します。
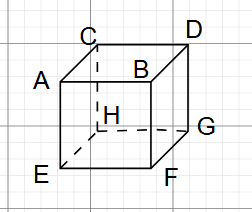
面ABDCに平行な面を考えます。平行とはどこまで伸ばしても交わらない関係なので面の場合は、どこまで広げても交わらない関係となります。
面ABDCと面EFGHはどこまで広げても交わらないので、この2つの面は平行です。
次に面ABDCと垂直な面を考えます。立方体は正方形で作られるので、全ての角が90°になっています。垂直とは直角で交わる関係なので、面EFGH以外の面は面ABDCと垂直に交わっています。
そのため面ABDCと垂直な面は、面ACHE、面ABFE、面BDGF、面CDGHとなります。
立方体や直方体ではある面に注目すると、平行な面は1つ、垂直な面は4つとなります。
次に辺どうしの関係を考えます。
辺ABと平行の関係にあるのは、辺CD、辺EF、辺HGとなります。
辺ABと垂直の関係にあるのは、点Aで交わる辺AC、辺AE、
点Bで交わる辺BD、辺BFがあります。
立方体や直方体ではある辺に注目すると、平行な辺は3つ、垂直な辺は4つとなります。
平行でも垂直でもない辺は、ねじれの位置なんて呼ばれたりしますが、現時点で特に知らなくても問題ないです。
最後に面と辺の関係を考えます。
面ABDCと平行な辺を考えます。すると辺EF、辺FG、辺GH、辺HEが平行となります。
面ABDCと垂直な辺を考えます。すると辺AE、辺BF、辺DG、辺CHが垂直となります。
立方体や直方体ではある面に注目すると、平行な辺は4つ、垂直な辺は4つとなります。
垂直な関係については、実際に分度器を使って測ってみるという経験もよいと思います。
今回一つの面や一つの辺に注目していますが、違う面や違う辺で考えても数
は同じになり、何か同じことをしているような感覚になると思います。
また立体図形の場合、縦と横に加えて高さというものが存在します。頂点の位置を縦、横、高さが何cmの位置にあるかで表すことができます。
下の図形を例に確認します。

頂点Aは横0cm、縦0cm、高さ0cmとなります。頂点Bは横は頂点Aから変わらず、縦に4cm、高さ5cm移動したところにあります。そのため頂点Bは横0cm、縦4cm、高さ5cmとなります。
頂点Cは頂点Aから横6cm、縦4cm移動し、高さは移動しない点なので、
頂点Cは横6cm、縦4cm、高さ0cmとなります。
立体図形の頂点は縦、横、高さという3つの数字で表せると認識してもられればと思います。
〇 展開図と見取り図
これまで立体図形を表すために使ってきた全体の図が分かるように書いた図を見取り図といいます。
それ以外にも立体図形を切り開いた図があり、これを展開図といいます。
段ボールなどの組立られる前の形状といったイメージです。この展開図
を線にしたがって折り、テープ等でくっつけると箱になります。
実際に箱を展開図から作る等して何度か体感してみてほしいです。

見取り図で確認できる面の数と面の形状が、展開図の線に囲まれた図形の数と形状に一致します。
見取り図では面が6つで形状はすべて正方形です。展開図でも正方形が6つあります。
日本の算数はこの分野の問題に妙にこだわって、妙に難しい問題がでることがありますが、代表的な展開図をいくつか見たことがあり、展開図と見取り図の面の数と面の形状に注目することがわかっていれば、その後の理系の学習にはそこまで影響がないのではないかと思います。
(妙に難しい問題とは、展開図のいろいろなパターンを見せて、この中で実際に見取り図の図形を作れるのはどれかや、どの点とどの点が重なるかなどの問題となります。)
ここまで記載する理由は、この分野が苦手な子がいるからです(私もそこまで得意ではなかったです)。
私が実務で役立ったのは、段ボールの組み立てくらいですが、手が覚えるのであんまり実務的にも利用しないことも多く、理系の分野でもそこまで使用した記憶がありません。
もちろんすごく興味を持つ子については、数学の特定分野に進むのも良いと思います。その結果、以下のようなことを思いつくかもしれません。ただ全ての子供が解ける必要性があるほどの重要性は無いように感じています。
どうしても解かないといけない人はこういったコツを紹介しているサイトもあるので、調べてみてほしいと思います。
[算数の問題]
以下の図形の面の形と数を答えてください。また展開図はA,B,Cのどれになるか答えてください。
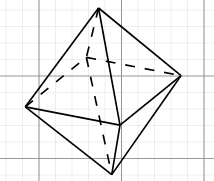

(答え)
この図形は三角形が上側に4つ、下側に4つくっついた形です。
(八面体と言われます。)
中央に四角形があるように見えてしまうのですが、立体図形を紙に書くときに発生してしまうもので、実物を見ると面として存在していないことが分かると思います。
自然界だとミョウバンの結晶は正八面体(面がすべて正三角形の八面体)なので、画像を検索してみるのもよいと思います。
展開図を考えるのは難しいと思いますが、三角形が8個ある展開図を探せばよいので、展開図Cが八面体の展開図と見つけることができます。
この問題は、展開図についてはこれくらいの難易度調整でよいのではないかという提案です。
(5)2つの変化する数量
〇 倍と割合
まず言葉を整理したいと思います。
「倍」という言葉は、同じ数字を重ねることです。使い方としては「3の2倍」などと表現します。そして3の2倍とは3を2回重ねることとなるので、3+3=3×2 となります。つまり「〇の△倍」とは「〇×△」をしたものということとなります。
次に「割合」という言葉について確認します。
割合とは二つの数量を比べた時に、一つがもう一つの何倍にあたるかという関係のことを言います。
例えば、「3の2倍は6です」という文章を見たときに、割合は2倍ということができます。つまり「〇の△倍」と言われたとき、「△倍」が割合ということとなります。
説明していて感じたのは、これは「データと図形」の分野ではなく、「数と計算」の分野ではないかなと思いました。
〇 関りをもちながら変わる数
世の中には「ある数」が変わったら「他の数」も変わるといったように関係性のある数どうしというものがよくあります。
例えばあなたがチケットを売っているとします。
チケットが1枚、400円だとして、売れたチケットの枚数(〇枚)と売り上げ(△円)を下の表にまとめています。この〇と△にはいろいろな数が入りますが、〇と△には適当にいろいろな数字が入るわけではありません。
例えば〇=2ならチケットが2枚売れているということになるので、売り上げ(△円)は800円となり、〇の数が決まれば△の数が決まります。

このケースには (売り上げ:△)=400×(売れた枚数:〇) という関係があります。この関係を〇や△で表すと、△=400×〇 となります。
ちなみに 〇=△÷400 、400=△÷〇 というように書いても、正しいです。(実際に表の中の数を入れて正しいことを確認してみてください。)
他の例としておこづかいが1000円のとき、お菓子に〇円使い、マンガに△円使いたいとします。表にいろいろな数字を入れた場合の結果を書いています。

この場合は、〇円を増やしたら、マンガに使える分は減るので、△円は減ります。そして足したときに1000円で変わらないという関係があります。
(おこづかい)=(お菓子代)+(マンガ代)となるので、1000=〇+△ という関係があります。
ちなみに〇=1000-△、△=1000-〇と書いても正しいです。
このように多くの数どうしは関りを持っています。これらの関係性を見つけることは実社会では難しいものが多いので、算数や数学のように「解けるように設定された問題」の中で訓練していってもらえればと思います。
また関係性を考えるときは、問題に指定がない限り、足し算やかけ算で関係性を探すとよいと考えています。
それは足し算やかけ算は数を逆にしても答えが変わらないのに対し、引き算やわり算は逆にすると答えが変わるため、関係を表す式が多く出てめんどくさいからです。
[算数の問題]
(問1)
ある八百屋で大安売りが行われていました。

① 普段のニンジンの値段は、大安売り中のニンジンの値段の何倍高いですか。
② 普段のダイコンの値段は、大安売り中のダイコンの値段の何倍高いですか。
➂ 大安売り中に値下がりした割合が高いのは、ニンジンとダイコンのどちらですか。
(問2)
1個400円のケーキがあります。買う個数(□個)と必要なお金(〇円)の表は以下の通りです。

黄色になっているところの数字を答え、「買う個数」と「必要なお金」の関係性を〇と□で表してください。
(答え)
(問1)
日本語のわかりづらいと感じる部分なのでコツを話すと、「〇〇はxx」のように書かれているとき、〇〇=xx と考えることができます。
そのため例えば①であれば、「普段のニンジンの値段」=「大安売り中のニンジンの値段を何倍かした値段」となります。
(普段の値段)=(大安売り中の値段)×(何倍)という関係性が見えたら、あとは(何倍)を求めるだけです。
① 50=25×(何倍) (何倍)=50÷25=2 したがって2倍が答えとなります。
② 150=50×(何倍) (何倍)=150÷50=3 したがって3倍が答えとなります。
➂ 割合が高いのは、①の「2倍」と②の「3倍」を比べて②のほうが高いことが分かります。そのため「ダイコン」が答えとなります。
(問2)
400×(買う個数)=(必要なお金) の関係があります。
黄色の場所は、3個買った場合の必要なお金ですから、400×3=1200
1200円となります。
〇と□で式を書くと、買う個数は〇、必要なお金は□なので、
400×〇=□ となります。
(6)折れ線グラフと表
〇 折れ線グラフ
これまでみてきたグラフに加えて、折れ線グラフというものを見てみたいと思います。折れ線グラフとはグラフの横方向の数直線(横軸)と縦方向の数直線(縦軸)にデータをとって、それを線でつないだものののことで、データの変化を見えるようにするために使われます。
2023年の東京で降った雨の量(降水量)を月ごとにまとめた表をもとに、折れ線グラフを作ったものが以下の図となります。


増え方が大きい5月と6月をみると、数値が上がっていて、折れ線の角度が大きいことが分かります。(オレンジ線を山だと考えると、5月から6月の間の線は登っていて、しかも登るのがきつそうに見えると思います。)
逆に減り方が大きい6月と7月をみると、数値が下がっていて折れ線の角度が大きいことが分かります。(オレンジ線を山だと考えると、6月から7月の間の線は下っていて、下るのが怖そうに見えると思います。)
このように折れ線グラフは表で見るよりも、データの変化が見えやすくなります。
(折れ線グラフの作り方)
1月は15.5mm雨が降っていることが分かるので、横軸が1、縦軸が15.5のところに点を描きます。2月は40.5mm雨が降っていることが分かるので、横軸が2、縦軸が40.5のところに点を描きます。それを繰り返して12月まで点をとってそれらを線でつないで折れ線グラフを作ります。
表を見て、点を方眼紙などに書いてみて実際に作ってみる経験をしてみてほしいと思います。ですが社会に出てからは、表計算ソフトなどで作る可能性が高いので、折れ線グラフからデータを読み取ることを重視したほうが良いと思います。
グラフは見やすくするためにあり、グラフを見て何か思った後は数字のデータを確認することが大切です。この「見えやすくすること」はグラフの作成者の考えで私たちの感覚をコントロールされているかもしれないからです。
以下の図は同じデータから作った折れ線グラフです。(縦軸の数字を変えています。)
左のグラフで「6月に雨が多い」ということを言ったり、右のグラフで「年間を通して降水量は安定している」と言ったりすることができそうだと感じると思います。

見える化することでデータ変化が分かりやすくなるのですが、それを利用してデータに関する私たちの感覚を操作できるという例です。
〇 2つの分類項目で整理した表
あなたが商品を考える部署にいるとします。商品A,B,Cがあって、それぞれの商品が男性と女性に対してそれぞれどれだけ売れているか知りたいとします。その場合、売れた個数を一つの項目(商品ごと)に分けた表を見ても分かりません。
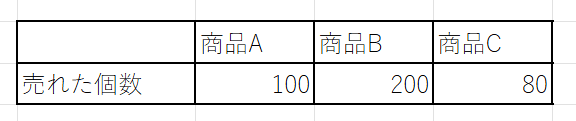
そこで売れた個数について商品と性別でそれぞれ分けた表を作ってみます。商品と性別の2つの項目で分けた表となります。

1項目の表では商品それぞれの売れた個数しかわかりませんでした。
ですが2項目の表では商品A,B,Cがそれぞれ男性にどれだけ売れたか、女性にどれだけ売れたかということが分かります。
男性に注目して横方向(→)に表をみていくと、商品A,B,Cが男性にどれだけ売れたかが分かります。また合計をみると、20+130+50=200 となり、男性に商品A,B,Cが全部でどれだけ売れたかが分かります。
次に商品Aに注目して縦方向(↓)に表を見ていくと、男性と女性にそれぞれいくつ商品Aが売れたかが分かります。そして合計をみると20+80=100となり、商品Aが売れた個数が分かり、これは1項目の表の商品Aの売れた個数と同じことが分かります。
また横方向(→)の合計も縦方向(↓)の合計も380で同じことが分かります。
横方向の合計は、(商品Aの売れた個数)+(商品Bの売れた個数)+(商品Cの売れた個数)となります。
縦方向の合計は、(男性に売れた個数)+(女性に売れた個数)となります。
結局、商品A,B,Cの売れた個数の合計の見方を変えているだけなので同じ個数ということになります。
[算数の問題]
(問1)
以下の表と折れ線グラフはある小学生の身長を学年ごとに記録したものです。
①小1から小6まで何cm身長が伸びたか答えてください。
②一番伸びた1年間は何年生から何年生の間で、何cm伸びたか答えてください。


(問2)
あるクラスで国語と算数について得意か不得意かアンケートを取りました。
(1) 黄色の部分(①、②)に入る数字を答えてください。
(2) 国語も算数も得意な人は何人いますか。また算数が不得意な人は何人いますか。

(答え)
(問1)
①折れ線グラフをみると、1年生から6年生まで身長はずっと伸びていることが分かります。
表データをみると小6の時142cm、小1の時115cmなので、伸びた身長は、
142-115=27cmとなります。
②一番伸びた時期は折れ線グラフを山とすると一番登るのがきつい場所です。そうすると小4から小5の間であることが分かると思います。
分からない場合、小1と小2の差、小2と小3の差のようにすべて表データから計算する方法でもよいです。
小5が138cm、小4が128cmなので10cm伸びたことになります。
(問2)

(1)
①:赤方向に見ると、①も②も数がわからないので、見ても分からなそうです。次に青方向で見ると、
「国語が不得意で算数が得意な人(7)」+「国語が不得意で算数が不得意な人(①)」=「国語が不得意な人(15)」 となっていることが分かります。
7+①=15 なので①は8人であることが分かります。
②:①の数が8だと分かったので、9+8=17 ②は17人だと分かります。
他にも、合計の↓方向に注目して、12+②=29 から②は17人と答えを出す方法もあります。
(2)
「国語も算数も得意な人」は、「国語が得意な人」を↓方向で見ていくと、「算数が得意な人(5)」と「算数が不得意な人(7)」という数字が見えると思います。
この中で国語が得意であり、算数も得意な人なので5人が答えとなります。
また「算数が不得意な人」の中には「国語が得意な人」と「国語が不得意な人」がいます。
そのため「算数が不得意な人」を→方向で見て、合計すれば良いことになります。その数は②なので、17人が答えとなります。
全体として思うこととしては「面積」はもう少し早い段階に持ってきた方が
いいと思います。
カーンアカデミーでも3rd gradeでは面積を説明しており、2ケタどうしのかけ算の計算も面積で説明しています。
私が子供のころはもう少し早く面積を学んだと思うのでカリキュラムが変化したのかなと感じました。
この記事が気に入ったらサポートをしてみませんか?
