
なぜ因数分解を勉強するのだろう? 文系の方向けのお話
なぜ因数分解を学ぶのだろう?
なぜ因数分解のような、将来一部の人にしか使えそうもない知識を学ぶのでしょう?
今回は中学で習う「因数分解」を例にして、なぜこんなことを学ぶのか、具体的に考えてみたいと思います。なお、技術職など理数系の知識を多く使う職をめざすのであれば数学や物理の知識は重要なので、今回は因数分解など使いそうもない方向けの説明です。(最近は分野が融合しており、文系・理系を分けることすらナンセンスですが、対比の意味で記載しています)
いろいろ考えた結果、5つの学びの段階ごとに、因数分解を勉強する意味を説明できるのではないか、と考えました。ちなみに因数分解とは、以下のような左辺→右辺の形にするやつですね。
$$
x^2+5x+6 = (x+2)(x+3)
$$
1)第一段階:棒暗記
公式を使ったりすることで因数分解ができること。また中学では、因数分解ができれば、二次方程式を解くことができるということ。もし因数分解できないなら解の公式を使えばいいということがわかり計算できる段階。
さらに高校では3次以上の方程式も出てきます。より複雑な公式や「たすき掛け」などが理解でき計算ができること。これを第一段階と考えたいと思います。問題を解く手続きやテクニックを知る段階です。
この段階の理解にいたれば、因数分解はテストや受験で、問題を素早く計算するために役に立ちます。
最近の教科書は大きく分厚くなり、非常に詳しくまとめられています。この第一段階の知識は、過去に学んだ知識の理解と、読み取る力さえあれば理解が可能です。
2)第二段階:他の知識とのつながりと利用
因数分解と、以下のような図形の面積を求める問題など、別の学習分野とのつながりが理解できる段階。単なる問題を解くテクニックから、因数分解という知識の利用ができる段階です。
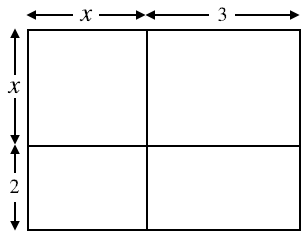
(面積)=(縦)×(横) = (x+2)×(x+3)
図形や関数、方程式などの複合問題は入試でもよく出てきます。2020年からの新しい学習指導要領では教科や単元をこえてさらに連携した問題が出てくるでしょう。
この段階の理解にいたると、因数分解を単なる計算問題としてではなく、他の学習分野に利用するのに役立ちます。
3)第三段階:抽象化と応用
因数分解を利用すれば、問題によっては二次方程式の問題を1次方程式の問題に分解することができるということです。
つまり、
$$
x^2+5x+6=0
$$
という二次方程式を
$$
x+2=0
$$
または
$$
x+3=0
$$
という一次方程式に分解するということです。
これは高次の問題を低次元化するということ、つまり「複雑な問題をそれぞれを構成する要素(の積)に分解して、簡単な問題にすること」と言い換えることができます。
私は塾をやる前は、科学技術計算(コンピュータシミュレーション)に長年たずさわってきました。多次元の非線形微分方程式の計算をそのまま行うと、たとえスーパーコンピュータを用いても膨大な計算時間がかかることがあります。そこで、必要とする計算精度ギリギリの範囲で低次元化して計算時間を短縮するということがよく行われていました。
例として、このことを商売に当てはめてみましょう。
商売でよく出てくる課題は「売上を上げるにはどうするか?」です。私も社会に出て営業として、マネージャーとして働く中で、さんざん考えてきた課題です。
このように複雑な要素のからむ問題をそのまま考えてもよくわからないので、一般には以下のように問題をより簡単な問題に分解して(因数分解して)考えます。
(売上)=(単価)×(個数)
「売上を上げるにはどうすればいいか?」という問題を、「単価を上げるにはどうすればいいか?」という問題と「個数を増やすにはどうすればいいか?」という問題に分けるわけです。
デカルトは「方法序説」の中で、以下のように言っています。
困難は分割せよ
もちろん、実戦ではこれでも大雑把すぎるので、販売のプロセスごと、製品ごと、チャネルごとなど、どんどん分解していきます。もちろん業界や製品により変わる公式です。例えば以下のような。(もちろん、実務ではもっともっと複雑です。)
(売上)=(単価)×{(集客数)×(成約率)}
ここで行なったのは、因数分解という数学で学ぶ知識を「複雑な問題を簡単な問題に分解すること」ととらえ、実際に起きている現実に当てはめて考えてみるということです。単なる計算問題として理解するのではなく、抽象化してとらえるという意味になります。
抽象化すればするほど具体的にイメージしにくくなりますが、本質に近づきます。本質というのは、他の分野に応用可能なので、因数分解という計算問題が、現実に応用できる知識になります。この認知過程をアナロジーといいます。
第二段階から第三段階への壁を超えると、学生時代の勉強が社会で活かせるようになります。
4)第四段階:知の境界を知る
テストや受験では、答えのある問題しか出ませんが、社会ではその知識が使える問題は限られます。上記の第三段階でいたった「複雑な問題を簡単な問題に分解すること」も頭を整理することには役に立ちますが、すべての課題を解決できるものでもありません。
例えば、恋愛がうまくいく法則というのは残念ながらよくわかりません。
(恋愛の成功)=(ルックス)×(性格)×(トーク)
とか、ある程度の因子に分解できるかもしれませんが、ナンパの達人であっても、万人に当てはまる恋愛の法則を知っているわけでもありません。
つまり今回の例でいえば、因数分解が適用できることは限界があることを知るということ、そしてその限界がどこにあるかを知るのが第四段階の理解と考えます。ギリシアの哲学者ソクラテスが「無知の知」といったことは有名です。
ここからさらに発想を広げれば、数学に限らずすべての分野において、人類が到達している現代の知識を総動員してもわかっていない領域があることを認めるということになります。そして、人類のもつ知と森羅万象との境界を知る、ということです。
最先端の研究を行なっている大学の先生、研究者や技術者がそれぞれの専門分野で到達している段階です。学会に行くと、人類が到達している知の境界を広げるために日夜試行錯誤がなされ、この研究ではどこを拡張できたかという会話がなされています。つまりイノベーションが起きています。
もちろん、数多くの先人達が何千年と培ってきた人類のもつ知の量は膨大です。一人の人間が一生の間に全ての分野の専門家になることは不可能です。
しかし、森羅万象はさらに果てしなく広大かつ深遠であり、それに比べれば、まだまだ人類は何も知らないに等しいと言えるのかもしれません。
私が知る大学の先生には謙虚な方が多いです。おそらく人類はここまではわかっている。でも、ここから先は明確にはわからない、という境界を理解されている、つまり人類にはまだまだわからないことがたくさんある、ということを実感されているからではないかと思います。
5)第五段階:暗黙知(タシット・ノウイング)
第四段階までは「頭」で考えることができ、さらに本や論文などの文章、数式などに落とせる領域です。「形式知」と言われたりします。意識の範囲で扱うことのできる領域です。
しかし人類にはさらに、説明できない、証明できない知の領域、経験や勘に基づく知識をもっています。ハートで感じたり、無意識で処理する領域です。
化学者・哲学者・社会学者であるマイケル・ポランニーは「何が正しいか、どこに答えがあるかはわからないが、自分がやっていることが正解に近づいているかどうかをジャッジする知が存在する」とし、それを暗黙知(タシット・ノウイング)と名付けました。(中土井僚さんと西尾泰和さんの対談から一部抜粋)
日本が誇る一橋大学名誉教授であり経営学者の野中郁次郎先生は「暗黙知」を「形式知」と対比させ、知識創造理論を構築され、情報化社会に続く、知識創造社会の礎を築かれました。
暗黙知の身近な例は「自転車に乗ること」です。どうやってバランスをとっているのか明確に説明しにくいですが、乗ることができる。
ベテランの職人や商売人、クリエイター、アーティスト、スポーツ選手などが、それぞれの専門分野においてこの段階の先端にいると考えます。もちろん有名でなくても、接客のプロのような方はたくさんいますよね。
南カリフォルニア大学のリチャード・クラークは「特定の分野に習熟するとその分野のことがいちいち意識にのぼらなくなる、ということが起こりやすい。ひとたび知識を習得すると、その知識について他人に説明するのは難しい。」と言っています。
また教育学者ウィン・ウェンガーによれば、顕在意識の情報処理は1秒間に126ビット。(ビットとは0と1で表せる2進数の桁を表す単位です。)一方、無意識では1000万ビットの情報処理能力を有すると言っています。暗黙知の領域は形式知に比べ、非常に複雑で深いことを示しているのではないでしょうか。
私としてはこの暗黙知までを含めて「人類の叡智」と呼べるのではないかと考えています。
因数分解の例でいえば、この段階では因数分解の限界は知った上で、複雑な問題を分解して考えるということが意識せずに高度に使える状態です。
よく定義や論点を曖昧にしたまま議論している場面に出会います。例えば、5年後のビジョンについてディスカッションをしているのに、「現状ではそんなことはできない。」という意見に終始してしまうとまとまらないことが多いです。論点を分解してディスカッションすれば、このようなことが起きにくいでしょう。
まとめ
「なぜ勉強するのだろう?」という疑問について、因数分解を例にして、教科書の勉強から社会につながる部分を考えてみました。
暗黙知の領域は、もしかしたら第一から第四とは同列ではなく並列的にとらえた方がいいのかもしれません。今回は難易度ではなく領域の広さという観点で記載しました。他に学んだ心理学やU理論などと整合性を整理できていない部分もありますし、もしかしたら第6の段階もあるかもしれません。
しかし一つ言えるのは、因数分解という中学数学で習う知識ですら、とらえ方によっては、意味を見いだすことができるという点です。
またこの暗黙知は、AI時代において別の可能性も感じます。
囲碁など一部はAIが人間を凌駕していますが、AIには越えなければならない技術的な課題があり、その一つはフレーム問題※といわれます。言葉で表せない暗黙の前提を考慮できないため、現在の技術の延長ではAIに到達できない領域といわれております。
人の感情や感性に関わる部分に加え、これからのAI時代に生きるヒントになるのではないでしょうか?
※フレーム問題を解決するニューロコンピュータなどの技術も開発が進められており、それらが解決するとAIが人間を凌駕するという見方もあります。
(本記事は2018年11月7日に書いたものです。Web改定にともない、noteに移植しました。)
もしこの記事が参考になったら、下のほうのハートマークをクリックしてくださいね。
この記事が気に入ったらサポートをしてみませんか?
