算数6年サピックス　デイリーサポート解説［61-19平面図形総合］

今回は角度や面積といった平面図形の復習が中心の回です。
比や相似を使った問題は特に頻出です。

★解説を読んでも分からない、授業中に板書を写せないお子様に。テキスト付属の解説はとても簡易的です。そこで家庭学習でお子様が取り組まれるデイリーサポート［実践編A〜E］について、お子様が1人で取り組めるような補助教材を作成しました。

・確認編全問対応
・豊富なカラー図表
・計算の過程も分かる

★著作権の関係で問題文そのものは掲載しておりません。万一誤字脱字、ご要望などございましたらコメント欄にお願いいたします。対応教材は順次増やしていく予定です。

---

今回学ぶこと

• アプローチ$${\textcircled{\small{1}}}$$面積比→A$${\fbox{3}}$$、面積比(応用)→A$${\fbox{5}}$$

• アプローチ$${\textcircled{\small{2}}}$$等辺と角度→B$${\fbox{1}}$$、おうぎ形の面積→C$${\fbox{1}}$$

• アプローチ$${\textcircled{\small{3}}}$$おりまげたときの重なり→B$${\fbox{3}}$$、長方形の重なり→C$${\fbox{2}}$$

• アプローチ$${\textcircled{\small{4}}}$$複合図形→B$${\fbox{2}}$$、弧の組合わせ→D$${\fbox{1}}$$

• アプローチ$${\textcircled{\small{5}}}$$平面の影→C$${\fbox{3}}$$、平行線の相似→C$${\fbox{4}}$$

• アプローチ$${\textcircled{\small{6}}}$$面積の割合→B$${\fbox{4}}$$、面積の割合(相似形)→D$${\fbox{2}}$$

• アプローチ$${\textcircled{\small{7}}}$$相似の組合わせ→D$${\fbox{4}}$$

• アプローチ$${\textcircled{\small{8}}}$$図形の重なり→E$${\fbox{4}}$$、方眼上の図形の面積→E$${\fbox{3}}$$

復習テキスト

• 41B-02角と角度(1)、H41-02角と角度(2)、41B-07図形のせいしつ、41B-13面積の考え方(1)、41B-14面積の考え方(2)、N41-01平面図形(1)、N41-02平面図形(2)、41B-27円とおうぎ形(1)、41B-28円とおうぎ形(2)、F41-01平面図形(1)、F41-03平面図形(2)

• 510-01平面図形(1)、510-02平面図形(2)、H51-03平面図形、N51-10円と多角形、510-26比と図形(1)、510-27比と図形(2)、F51-02平面図形、510-37平面図形総合

• 61-02平面図形、H61-02平面図形

実践編A

$${\fbox{1}}$$

2つの二等辺三角形に注目します。
赤い二等辺三角形の2つの角(㋑)の和は180°−74°＝106°なので、㋑＝53°です。  

・スリッパの法則：三角形の外角は、隣り合わない2つの内角の和と等しい

ここで、㋐+㋑＝74°であることに注目すると、㋐の大きさを求めることができます。

$${\fbox{2}}$$

面積を求めやすいように等積変形します。

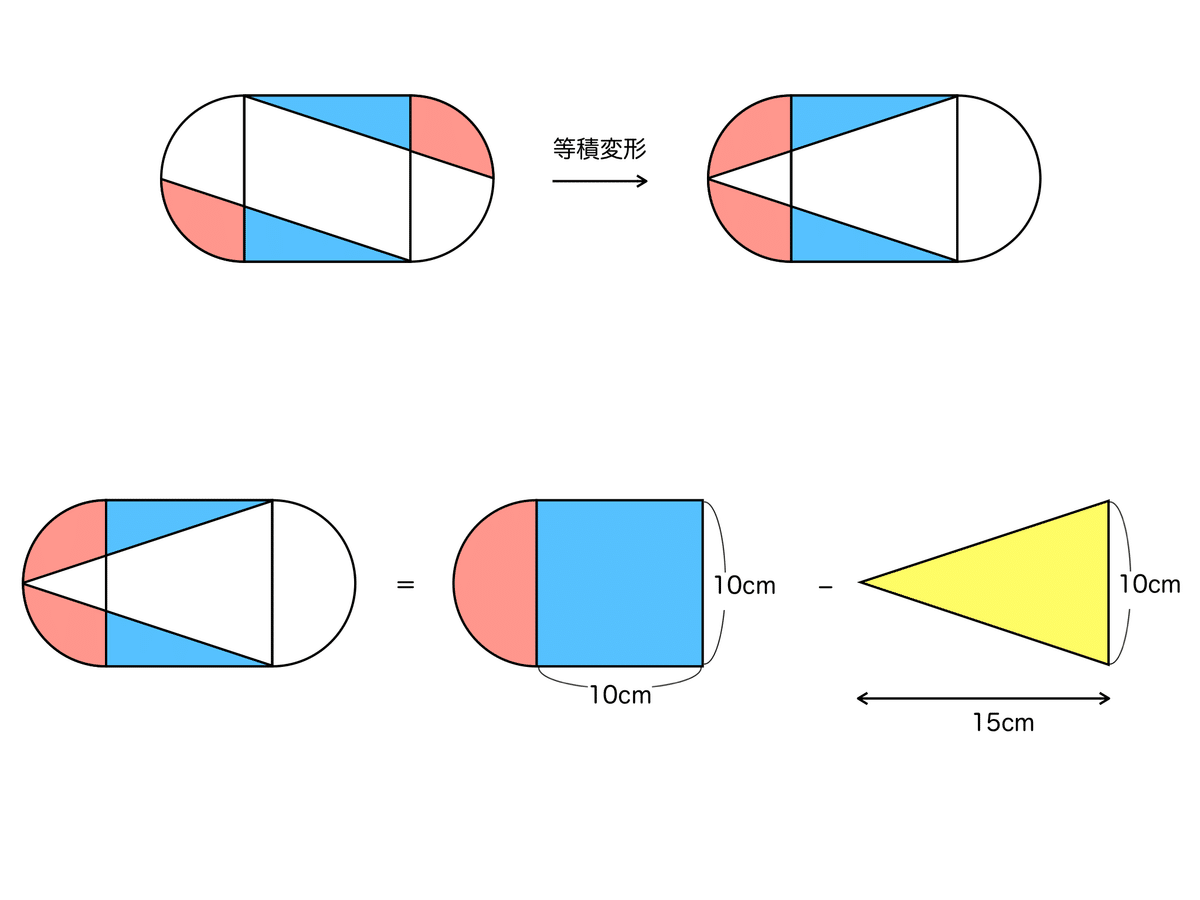
半径5cmの半円と1辺10cmの正方形から、底辺10cm・高さ15cmの三角形を引くことで求められます。

5cm×5cm×3.14×$${\tfrac{1}{2}}$$+10cm×10cm−10cm×15cm÷2

・3.14の計算のポイント
「25×3.14＝78.5」はよく使うので覚えておきましょう
「12.5×3.14」はその半分で、39.25と求められます

$${\fbox{3}}$$面積比

三角形全体の面積を1として、3つの三角形の面積を引いて求めます。

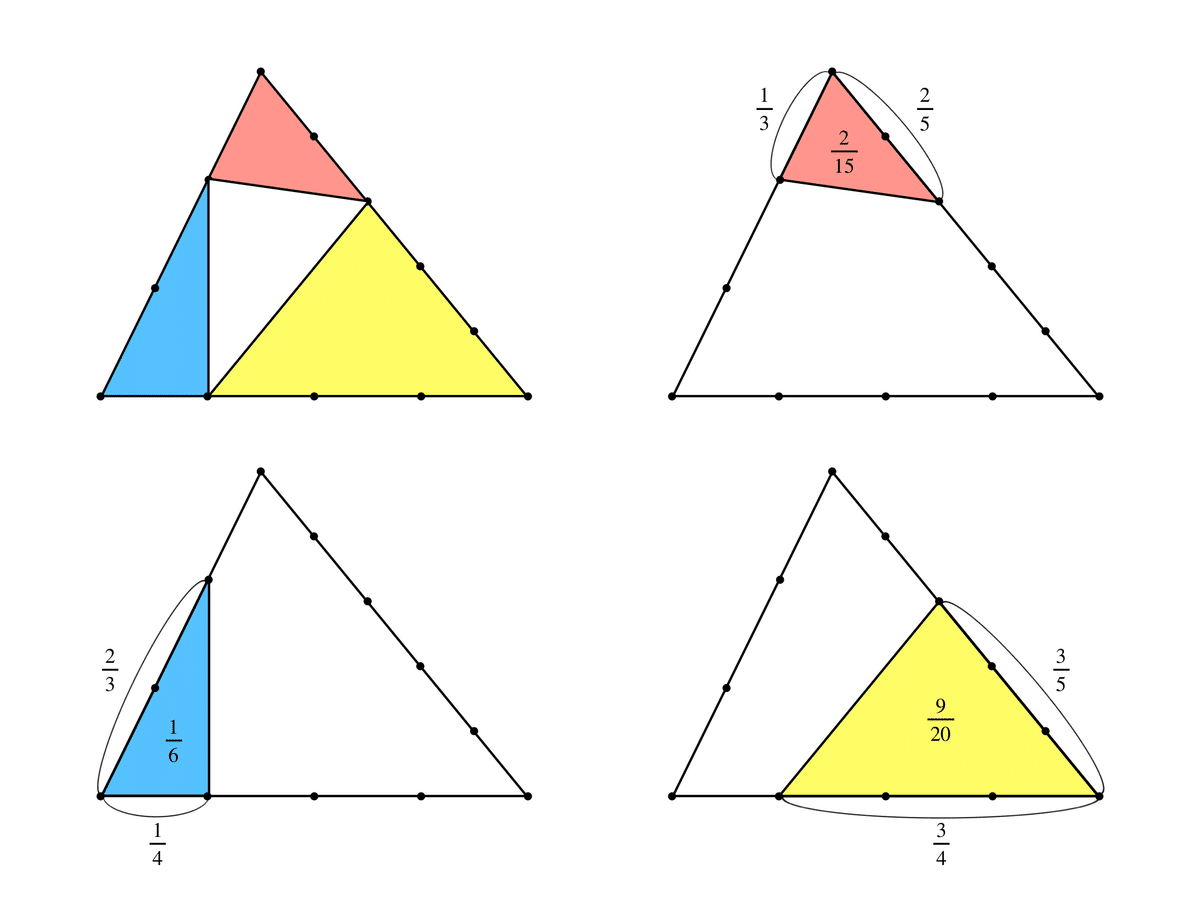
・赤色の三角形
三角形全体の面積の$${\tfrac{1}{3}}$$×$${\tfrac{2}{5}}$$＝$${\tfrac{2}{15}}$$倍なので、面積は$${\tfrac{2}{15}}$$です。

・青色の三角形
三角形全体の面積の$${\tfrac{1}{4}}$$×$${\tfrac{2}{3}}$$＝$${\tfrac{1}{6}}$$倍なので、面積は$${\tfrac{1}{6}}$$です。

・黄色の三角形
三角形全体の面積の$${\tfrac{3}{4}}$$×$${\tfrac{3}{5}}$$＝$${\tfrac{9}{20}}$$倍なので、面積は$${\tfrac{9}{20}}$$です。

3つの三角形の面積の和は、$${\tfrac{2}{15}}$$+$${\tfrac{1}{6}}$$+$${\tfrac{9}{20}}$$＝$${\tfrac{8+10+27}{60}}$$＝$${\tfrac{3}{4}}$$です。

$${\fbox{4}}$$

面積を求めやすいように等積変形します。

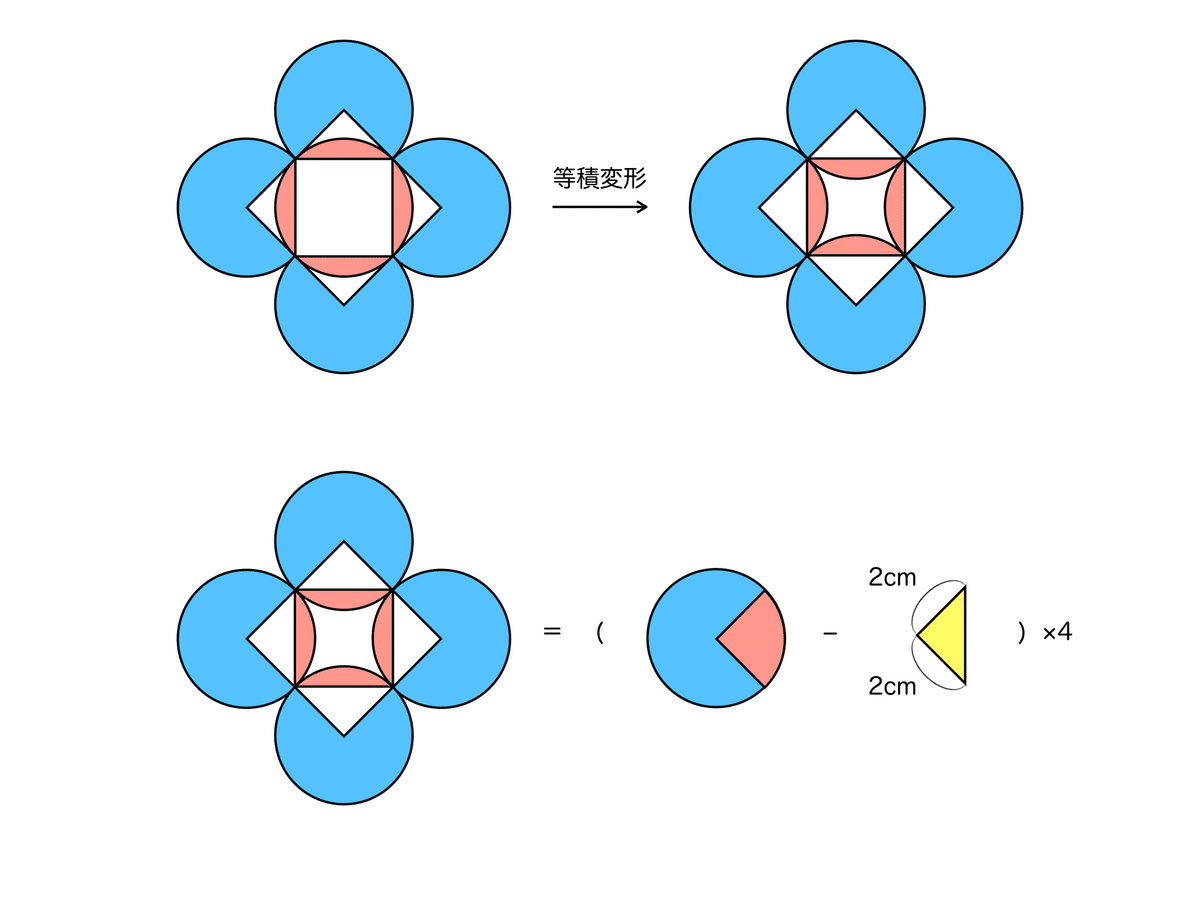
半径2cmの円から1辺2cmの直角三角形を引いた形が4個分です。

(2cm×2cm×3.14−2cm×2cm÷2)×4個＝16×3.14−8

・3.14の計算のポイント
3.14はできるだけまとめて最後に計算しましょう
「16×3.14＝50.24」はよく使うので覚えておきましょう

$${\fbox{5}}$$面積比(応用)

・赤色の三角形
三角形全体の面積の$${\tfrac{3}{4}}$$×$${\tfrac{1}{4}}$$＝$${\tfrac{3}{16}}$$倍です。

・青色の三角形
三角形全体の面積の$${\tfrac{2}{3}}$$×$${\tfrac{1}{4}}$$＝$${\tfrac{1}{6}}$$倍です。

・黄色の三角形
三角形全体の面積の$${\tfrac{3}{4}}$$×$${\tfrac{1}{3}}$$＝$${\tfrac{1}{4}}$$倍です。

(1)青色の三角形の面積は三角形全体の面積の$${\tfrac{1}{6}}$$倍なので、2880㎠×$${\tfrac{1}{6}}$$倍で求められます。

(2)3つの三角形の面積の和は、三角形全体の面積の$${\tfrac{3}{16}}$$+$${\tfrac{1}{6}}$$+$${\tfrac{1}{4}}$$＝$${\tfrac{9+8+12}{48}}$$＝$${\tfrac{29}{48}}$$倍です。

よって、真ん中の三角形の面積は、三角形全体の面積の1−$${\tfrac{29}{48}}$$＝$${\tfrac{19}{48}}$$倍です。

内側の三角形でも同じように考えることができます。

よって、真ん中の白い三角形の面積は、三角形全体の面積の$${\tfrac{19}{48}}$$倍のさらに$${\tfrac{19}{48}}$$倍です。

2880㎠×$${\tfrac{19}{48}}$$倍×$${\tfrac{19}{48}}$$倍

★実践編B以降は有料(500円)でご覧いただけます。