SIRモデル・SZRモデルの数的解析 ある時点におけるゾンビの感染拡大可能性を調べる(前編)
前回の記事
前回の記事では、SIRモデルとSZRモデルを方程式に落とし込み、式変形を行うことによってゾンビパンデミックが起こりうるかどうかを議論した。しかし使用した解析手法は高校数学レベルであったので、初期状態からゾンビパンデミックが起こるかどうかを予想することが精々だったうえに、ごく単純なモデルにしか使えない(同じようにSIZRモデルを式変形で解析しようとしたが、全く芳しくなかった)。
今回の記事では前後編にわけて、少々難しい数学を用いて解析を行い、ある時点において人間やゾンビが増えるか減るかを議論できるようにしたい。
結論を言っておくと、SZRモデルからヤコビ行列を作り、その固有値にS、Z、Rの各値を代入することで、安定性を調べる、ということだ。
連立微分方程式
前回の記事ではSZRモデルを次のような方程式で表した。
S'=-βSZ
Z'=βSZ-αSZ
R'=αSZ
この三式は上から人間、ゾンビ、死体の一日当たりの増加量を表す方程式だった。この式を次のような式に書き直す。
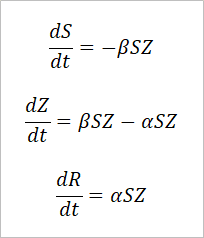
それぞれの左辺に(d/dt)という文字を追加した。これはわかりやすい言葉に直せば「tで微分した」ということだ。微分は高校数学に出てくるので馴染みの人も多いと思うが、一応日本語で丁寧に説明しておくと「tがちょっと増えたときにSやZ、Rはどれだけ増えるのか」という意味である。「素人質問なのですが、『ちょっと』とはどのくらいなのでしょうか」という声が聞こえてきそうだ。
また、tは経過時間を意味する(timeの頭文字)。したがって、(d/dt)とは「時間がちょっと経ったときの対象の増加した量」を表すのである。上記式のケースでいえば対象とはSやZ、Rのこと。専門的な言い方をすると、「単位時間当たりの〇〇の増加量」となる。
前回の記事では左辺を「一日あたりの~の増加量」などと言葉で表記したが、数式を使えば上記のように端的に表せる。数学は便利だ。
さて、上記式は方程式だった。微分を含む方程式は微分方程式と呼ばれる。さらに言えば方程式が複数並んでいるので、連立方程式と呼ばれるべきだろう。したがって、SZRモデルを表す式は連立微分方程式ということになるだろう。
中学で習う方程式は、謎の文字xやyの正体はどんな数字か暴く(解を求める)ことが目的だった。しかし微分方程式の場合、解を求めるというのは数字ではなく関数を求めることだ。SZRモデルでいえば、tを使った式でS、Z、Rを表すというのが解を求めることに相当する。
ただし、tを使ったひとつの関数でSZRモデルを表すことはできない。右辺が複雑すぎるからだ。ZがSに比べて無視できるほど小さい場合や、その逆の場合など、条件を限定すれば可能なのだが…。
ということで、関数を作らずにSZRモデルの連立微分方程式を解析していこう。
連立微分方程式の行列表記 ヤコビ行列の導入
まず、中学校で習う一般的な連立方程式はベクトルと行列の積で表せる。具体例をひとつ見せよう。下記式は簡単な連立方程式をベクトルと行列で書き直したものである。
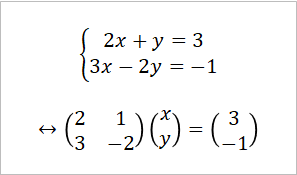
上記の式にはかっこが3つ出てきている。そのうちx, yと3, -1が縦に並んでいる2つがベクトルで、2x2の合計4つのいろいろ数字が入っているのが行列である。ベクトルである(x, y)を行列で変換すると、(3, -1)というベクトルになりますよ。(x, y)の正体は何ですか?というのが上記式の意味だ。
ここでいうベクトルとは要素のセットのことだ。連立方程式の解はxとyのセットで書くので、であれば最初からセットで表記しておこうと。そういうことだ。ほかでは座標内の点(x, y)などがセットとしてなじみ深いだろうか。実はこいつら、すべてベクトルだったのだ。
次に行列だが…今回はひとまず行列とはベクトルを変換するものなのだと説明させてほしい。上記式では、ベクトルの(x, y)を(3, -1)に変換しているが、ほかにも、ベクトルの中身をすべてあるいはひとつだけを選んで2倍3倍にするといった単純なものから、ベクトルの内容数を増やしたりセット内容の単位を変えたり(たとえば人口から人口密度へ)といった多少難しいものまでいろいろなものを含む。
では次は、前節で連立微分方程式にしたSZRモデルを行列とベクトルで表そう。何をベクトルにすべきか。ここはS、Z、Rのセットをベクトルとしてひとまとまりにするべきだろう。
左辺のS、Z、Rはtで微分されているので、ベクトルを使えば下記式のように書き換えられる。最後の式が(S, Z, R)からxにまとめられているのは、その方がしゅっとしていて見やすいからだ。
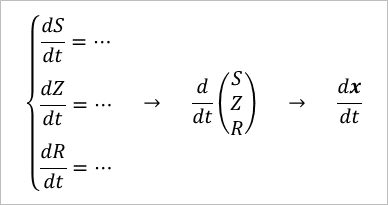
次は右辺だ。右辺もやはり(S, Z, R)をまとめたxベクトルを使って表したい。ベクトルと行列を使って右辺を表したい。この場合、行列の役割は「xベクトル」を「時間微分されたxベクトル」へ変換することになる。
役割がわかればあとは作るだけだ。導入したxベクトルはS、Z、Rの3要素なので、上述した連立方程式の具体例とは違って、SZRモデルの行列は3x3の9要素で構成されるべきだ。さくっと作ろう。
と、言いたいところだが…SZRモデルの連立微分方程式をベクトル表記にすることはできない。右辺を見るとSとZの積が並んでいる。なんと、(S, Z, R)ベクトルを使ってS×Zを表すことはできないのだ。SとZが分離していれば可能なのだが…。
しかし、行列の役割…すなわち(S, Z, R)にどのような変換を行えば(dS/dt)や(dZ/dt), (dZ/dt)が出てくるのか考えることはできる。
たとえば、S、Z、Rに何をかければ(dS/dt)になるだろうか。SZRモデルから作った方程式によると、(dS/dt)=-βSZなので、Sには-βZ、Zには-βSをかけてやればよい。残念だがRには何をかけても(dS/dt)にならないので、無関係のしるしにゼロをかけることにしよう。
S ×(-βZ) → (dS/dt)
Z ×(-βS) → (dS/dt)
R ×0 ((dS/dt)とは無関係なので)
また、(dZ/dt)や(dR/dt)についても、S、Z、Rに何をかければよいのか?を考えれば行列の内容を決められる。このようにして決めた行列を下に示す。
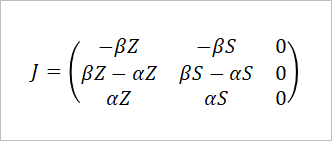
一番上の行が左からS、Z、Rを(dS/dt)に変換するための要素で、真ん中の行がやはり左からS、Z、Rを(dZ/dt)に変換するための要素、となれば一番下の行は…?そう、一番下にあるのはS、Z、Rを(dR/dt)に変換するための要素だ。
これが(S, Z, R)のセットであるxベクトルを(dx/dt)へ変換する行列だ。行列とベクトルの計算法を知っているならば挑戦してほしいが、この行列とxベクトルを計算してもSZRモデルの連立微分方程式を再現することはできない。しかし、「どういう変換をしたのか?」のエッセンスは詰まっている。このような行列をヤコビ行列という。上でヤコビ行列をJで表しているのは英語でヤコビ行列はJacobianと書くからだ。
以上、SとZとRをベクトルとしてひとつにまとめ、行列を使って連立微分方程式をベクトルと行列で表せるようにした。
SZRモデルを感染期をはさむSZRモデル(SIZRモデル)や隔離あり・治療ありSIZRモデルへ変更する場合はベクトルにIやQを追加し、モデルの連立微分方程式に合わせてヤコビ行列の内容を変更すればよい。
この時点で、ヤコビ行列を用いた手法は前回の記事で紹介した式変形を用いた解析よりも優れていることが確定した。式変形では隔離ありSIZRモデルや治療ありSIZRモデルはおろかただのSIZRモデルすら解析困難を極めたからだ。
後編へ続く。が…
結構な文量になったし、高校あたりで数学を勉強しなくなった人を想定して記事を書いているので、ここまでを前編として残りの解析内容は後編に続くこととする。
後編ではヤコビ行列の解析法を具体例を交えて紹介する予定だ。行列の固有値を説明し、固有値を用いた解析法を具体的に紹介しよう。
ちなみにだが…高校どころか大学に行っても数学を勉強し続けた方にお聞きしたい。ヤコビ行列もといヤコビアンは線形代数と微積分どちらに属するのだろうか。私の記憶しているヤコビアンはdxdydz=r^2sinΘdrdΘdφなので、SZRモデルの論文を読んだ際に行列で出てきたヤコビアンを見てとても驚いてしまった。
そもそもヤコビアンとは何なのか。出自は線形代数?それとも微積分?年収は?結婚はしてるの?調べてみましたがわかりませんでした。勉強中なので、コメントいただけるとうれしいです。
参考
この記事を書くにあたって参考にした本を2冊紹介する。前者の読破には大学1年生修了レベルの数学の知識が必要だが、後者は数学アレルギーさえなければどうにか読める(ほんと?)。
後編
この記事が気に入ったらサポートをしてみませんか?
