
コラッツ予想を無限公理と背理法で証明(preprint)
前は、ペアノ公理でコラッツ予想の証明をしたが、帰納法では無限に続く任意の自然数に対して満足しないので、無限公理と背理法を用いて一般教養レベルで解るように証明してみる。証明の各段落は、正の整数の集合から始まり、奇数の2倍数列の分類、奇数の型式、数列の関連性、そしてボトムアップのプロセスを経て、最終的にコラッツ予想の成立を結論づけます。
1,正の整数の無限集合
前提として正の整数の無限集合があり、部分集合を定義することで空集合{}が空であることにより、無限と0の対比できる集合ですね。
{},1,2,3・・・
正の整数の無限集合に関する前提は、無限公理を用いて以下のように述べることができます。
無限の公理(Infinity Axiom): ある集合 x が存在して、空集合 ∅ が x の要素であり、かつ任意の y が x の要素ならば、S(y) も x の要素となる。
2,奇数の2倍数列
奇数と偶数の部分集合の分け方として、奇数の2倍数列でわけます。
{1,2,4,8,16・・・}
{3,6,12,24,32・・・}
{5,10,20,40,80・・・}
※これにより偶数なら1/2するコラッツ計算をすべて含み、残る奇数の2倍数列間のつながりはコラッツ計算による3x+1しかないことになる。
3,奇数には4n+1型式と4m+3型式の奇数がある
4n+1型:1,5,9,13,17・・・
4m+3型:3,7,11,15,19・・・
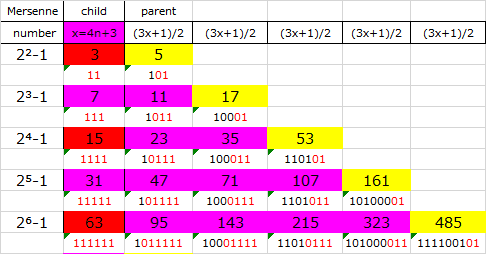
4,4m+3の2倍数列を4n+1の2倍数列別に集合化
x=4m₁+3型の奇数は、3x+1=12m₁+10→6m₁+5の奇数になり、
m₁が奇数なら、6m₁+5=4m₂+3型の奇数になり、7=4(1)+3→11=4(2)+3、
m₁が偶数なら、6m₁+5=4n+1型の奇数になり、11=4(2)+3→17=4(4)+1、
結果、4m₁+3型の奇数<4m₂+3型の奇数<4n+1型の奇数にリンクするので、すべての4m+3型の奇数は、最終的により大きい4n+1型の奇数(m=[n-1]/3が整数)の2倍の元へ単射する。
※これにより、4n+1型式の奇数の2倍数列にすべての4m+3型式の奇数の2倍数列が紐づき、残る4n+1の奇数の2倍数列間のつながりはコラッツ計算による3x+1しかないことになる。
5,4(0)+1=1の2倍数列を0世代と定義
{1, 2, (4), 8, (16), 32, (64), 128, (256), …}
※ ()は4(3n+1)=12n+4形式の元
6,0世代の12n+4形式の偶数は1世代の4n+1型式の奇数と単射
12n+4の偶数を、-1して3で割ると4n+1の奇数になる。
12(1)+4→(16-1)/3=5=4(1)+1
この4n+1型式(n=0を除く)の奇数5や21や85・・・を1世代とする。
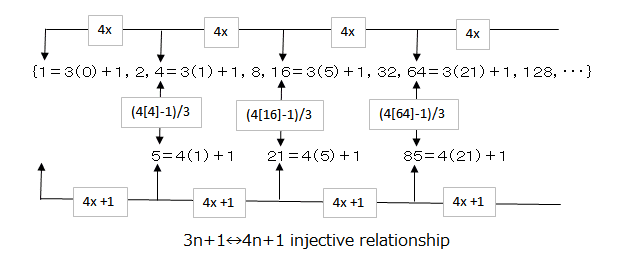
一つの奇数の2倍数列から次の世代の奇数の2倍数列へ3n+1→4n+1の単射関係があることと、次の世代の奇数の2倍数列同士に4n₂+1=4(4n₁+1)+1の関係があるのは、どの世代にも共通するルールです。
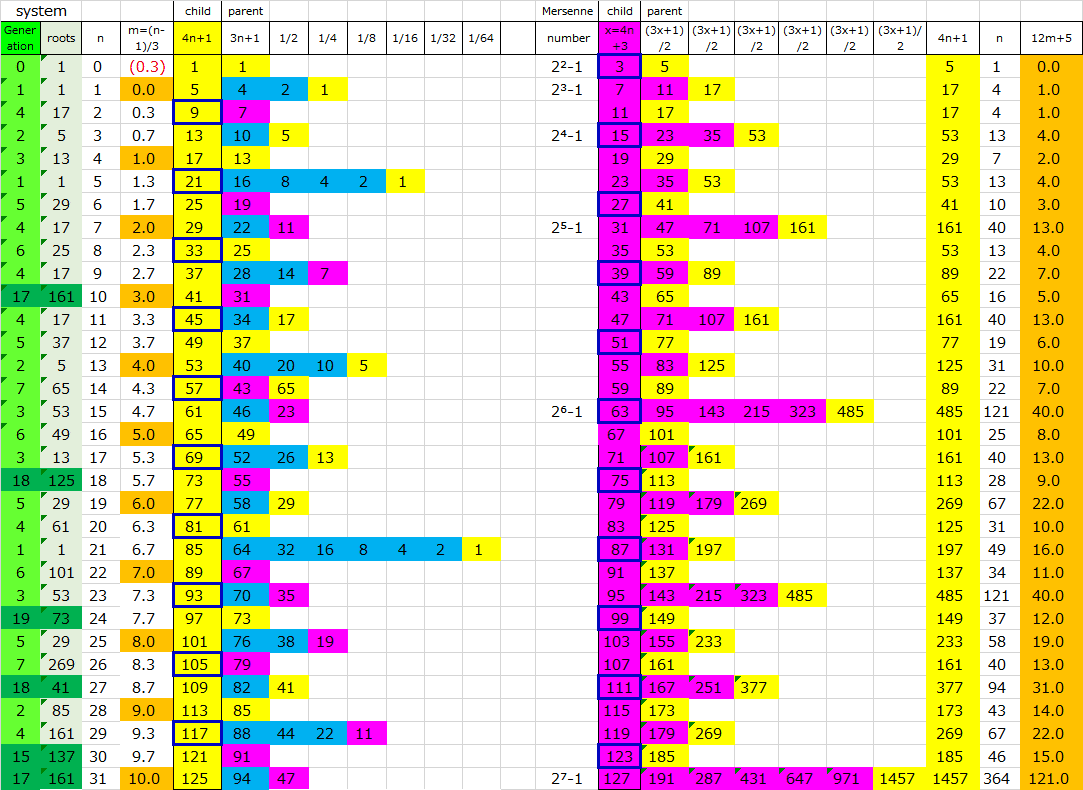
7,0→1→2世代へボトムアップを繰り返すと、すべての4n+1の奇数別の部分集合は0世代にツリー構造でつながる。
したがって、任意の正の整数をコラッツ演算すると1世代1つの4n+1の奇数がつながり、この4n+1の奇数をラベルとする部分集合のツリー構造により0世代のn=0の4(0)+1=1,2,4のループになる。

結論
以上により、コラッツ演算で4n+1と3n+1が縮小方向へ単射関係があることと、コラッツ逆演算で1からボトムアップすると4n+1の部分集合の入り口は4n+1だけなので、常に新しい4n+1の部分集合にしかつながらないので、ループがなく無限方向に発散する。この2つの関係を背理法を用いて考えると、1の2倍数列を無限方向に展開した場合、すべての4n+1型の奇数と別の4n+1型の奇数がツリー構造でつながらないのは矛盾するので、コラッツ予想は正しく無限公理と正の整数の性質から説明可能であることが示される。
追加情報
この証明では、すべての自然数は有限回の演算を通じて 1 の値に到達すると主張する弱いコラッツ予想の妥当性を実証しました。 ただし、強力なコラッツ予想によって提案されている、1 に到達するために必要な正確なステップ数と世代数に関する具体的な詳細は、この証明では取り上げられていません。
非常に複雑な数学的問題である強力なコラッツ予想は依然として証明されておらず、現在の数学的知識の領域における課題であることに注意することが重要です。 この長年の疑問を解決するために、現在進行中の研究が進められています。 この証明により、弱いコラッツ予想についての理解が大きく前進しましたが、強いコラッツ予想を追求するにはさらなる調査が必要です。
参考:
査読ジャーナルへの投稿の推薦状お願いします。
重大な未解決の問題を解決すると主張する提出物(例: ゴールドバッハの予想;ギルブレスの推測; ビールの推測;無限に多くの双子素数。 リーマン仮説;3x + 1または「コラッツ」問題) または、フェルマーの最後の定理などの主要な結果の前に、物理的な手紙(電子メールではない)を書面にする必要があります 関連する専門知識を持つ博士号の数学者によって署名され、 著者の一人以外、 大学での予定、そのレターヘッドに 大学、および通常の郵便で送られ、 彼/彼女が論文を読んだと述べて、すべてを理解しています その中に提示された議論、そしてその正しさを証明します。 https://cs.uwaterloo.ca/journals/JIS/
知恵袋でのやり取り
この記事が気に入ったらサポートをしてみませんか?
