
待ち時間について考える方法
基本情報技術者試験では、午前試験のテクノロジ系で応用数学も問われます。
今日、その応用数学の勉強に入ったのですが、その中で出てきた
「待ち行列理論」
をきちんと理解しようという目的でnoteを書こうと思います。
せっかくなので、薬局を舞台にしてみようと思いますが、そこ違うよってところがあれば、教えてくださいませ。
ただし、ポアソン分布とか指数分布についてまでは言及しませんので悪しからず。
待ち行列理論とは?
待ち行列理論(まちぎょうれつりろん 英語: Queueing Theory)とは、顧客がサービスを受けるために行列に並ぶような確率的に挙動するシステムの混雑現象を数理モデルを用いて解析することを目的とした理論である。応用数学のオペレーションズ・リサーチにおける分野の一つに数えられる。
電話交換機や情報ネットワーク、生産システム、空港や病院などの設計や性能評価に応用される。
まず、この言葉を聞いて思ったのは、そのまんまやなってことですね。こういう理論めいたのって、結構難しい言葉を使っていて、いざ勉強してみたら、そんな難しい名前にせんでもええのにっていう理論も多いのですが、こと「待ち行列理論」に関しては、そのままだなっていう印象を持ちました。
なので、この理論は好きです。
待ち行列とは、そのまんま「待っている人の行列」のことです。
で、ここで思いますよね。
「えっ?基本情報技術者試験ってIT系の試験じゃないの?」って。
そうなんです。僕が受けようとしているのは、基本情報技術者試験。
ゴリゴリのIT関連の資格試験です。
ですが、この「待ち行列理論」。IT系の資格で結構大事な理論のようで、基本情報技術者試験だけでなく、その後に挑もうと思っている応用情報技術者試験でも頻出されるらしいです。
M/M/1モデル
「待ち行列理論」については、先人達が色々なモデルを考えたためちょっとわかりにくくなっていた時期もあったようです。そこで、多くのモデルをわかりやすく表現しようとしたのが、D.G.ケンドールさんという方です。
で、その表示方法を「ケンドールの記号」と呼びます。
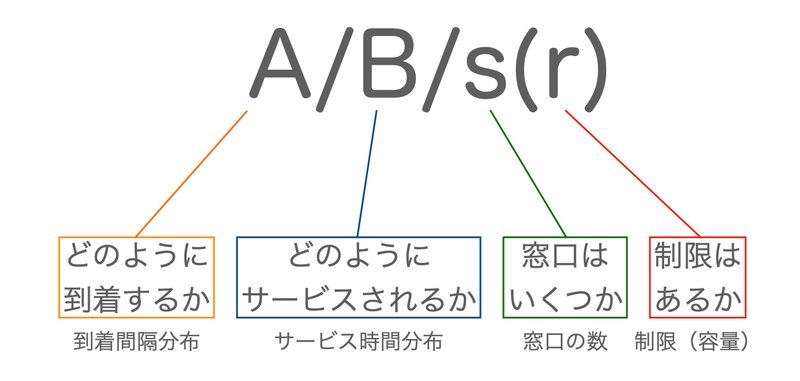
その中で一番シンプルなモデルが、M/M/1モデルと言われるものです。
(MはMarkovianの頭文字,1は窓口の数を表します。)
他にもM/M/2モデルとかD/M/1モデル、M/E/1モデルなどもあるらしいのですが、その辺の詳細は割愛させていただきます。(ただ単にまだそこまで必要なさそうなのです。)
M/M/1モデルは、イベントが完全にランダムに起こる状況について考えているモデルで、病院や薬局の待合室で、どれくらい待つんだろう?という状況や切符売り場や銀行のATMでどうすれば待ち時間が少ない効率の良くできるのかを理論的に考える状況が例に挙げられます。
薬局薬剤師にとっては、患者さんの待ち時間をどうやったら短縮でき、患者さんの大切な時間を奪わないで済むか?というのは、非常に大事な課題です。
正直なところ、単純に確率論では考えられない部分は大いにありますが、今回は、待ち行列理論を理解するために、シンプルに考えてみようと思います。
待ち行列理論(M/M/1モデル)で分かること
では、M/M/1モデルで一体何が分かるのでしょう。僕が病院や薬局、人気のラーメン屋さん、給料日のATMなど様々な行列に並ぶ時に知りたいのは、
「どれくらい待つのか?」
です。
で、M/M/1モデルでわかるのは、「平均何人分待つのか?」で、それさえ分かれば、「平均どれくらい待つのか?」が分かるんです!(って今日知ったところです。)
その式が、こちら
待ち時間 = ρ / (1 - ρ) (人分)
です。
これは、自分の前にはすでにρ/(1-ρ)人が並んで待っているということで、これに、後で出てきますが、「平均サービス時間Ts」をかけると、平均待ち時間が分かります。
平均待ち時間 = ρ / (1 - ρ) × Ts
ρって何?
ちょっと待ってください。
さっき、急に出てきましたが、このρって一体何だって話ですよね。
この急に現れたρ。これは、「混み具合」を表しています。僕が勉強させていただいているスタディングでは、「利用率」と表現されていました。他のサイトでは、「平均稼働率」と表現されている方もいらっしゃいました。
では、この「混み具合(利用率・平均稼働率)」について考えたいと思います。
そのためには、もう少しだけ用語を知らないといけませんが、言葉そのものは全然難しくはありません。
◯ 平均到着率 = λ [人/時間]
◯ 平均サービス率 = μ [人/時間]
◯ 利用率・平均稼働率 = ρ = λ / μ
まずは、平均到着率(λ)です。
平均到着率(λ)は、単位時間あたりに到着する人数のことで、簡単に考えると「1時間に何人患者がくるか」という量です。
薬局の場合、午前の開局中(9:00〜13:00)に40人患者さんが来られれば、その平均到着率(λ)は、
平均到着率 = λ [人/時間] = 40人 / 4時間 = 10人/時間
となります。ちなみにこの逆数のことをTa = 平均到着時間といい、「何時間ごとに患者さんが来るか」という量になります。
(この場合だと、Ta = 1 / 10 = 0.1(時間/人)= 6(分/人)ということになります。)
次に、平均サービス率(μ)です。
平均サービス率(μ)は、単位時間あたりにサービスを受けることのできる人数のことで、単純化すると「1時間に何人の患者さんに投薬できるか」という量です。
薬局の場合、午前の開局中(9:00〜13:00)に48人投薬できれば、その平均サービス率(μ)は、
平均サービス率 = μ [人/時間] = 48人 / 4時間 = 12人/時間
ですね。
そして、こちらの逆数のことをTs = 平均サービス時間といい、「1人あたり何時間掛かるか」という量になります。
(この場合は、Ts = 1 / 12 (時間/人)= 5(分/人)となります。)
そうするとρを求める計算は、
利用率・平均稼働率 = ρ = λ / μ = 10 / 12 = 5/6 ≒ 0.833
となり、利用率・平均稼働率(ρ)は、0.833ということになりますね。つまり混み具合は、約83.3%ということです。
待ち時間はどれくらい?
ρの計算ができたので、次は、待ち時間(人分)の計算です。
先程の式に代入しますと、
待ち時間 = ρ / (1 - ρ) = 5/6 / (1-5/6) = 5(人分)
で、待ち時間は5人分ということになります。
そして、この薬局の平均サービス時間Tsが5分/人ですので、結果、平均待ち時間は、
平均待ち時間 = ρ / (1 - ρ) × Ts = 5 × 5 = 25分
となります。
この薬局にある患者さんが入って来て、処方せんを受け取った後、その患者さんの名前を呼ぶまでに平均して25分かかるという結果になりました。
また、投薬を受け終わるまでの時間のことを「ターンアラウンド」タイムと言うのですが、そこまで含めると
ターンアラウンドタイム = 25分 + 5分 = 30分
ということになります。
つまり、この薬局にある患者さんが入って来て、処方せんを受け取った後、その患者さんにお薬を渡し終わるまでに平均して30分かかるということですね。
実際は、もうちょっと早めにお薬をお渡しできた方がいいですね。
ポアソン分布と指数分布
本当は、この類の問題には、但し書きが必要なんですが、その辺は、今回は触れません。その但し書きは、来局患者数はポアソン分布,投薬数は指数分布に従うというもので、このポアソン分布はめちゃくちゃ大事な離散確率変数です。(指数分布は連続確率変数でした。)
今後、ITストラテジストに向けて勉強を進めていく中で、より理解を深めていければなど思っているところですが、今は、ご説明できるほどには理解できておりません。。。
先はまだまだ長いですね。
今日もお付き合いいただきましてありがとうございました。
また、明日。
この記事が気に入ったらサポートをしてみませんか?
