物理量が作用素になるのは、古典力学でも同じ。

「物理量を演算子にする」という考え方は量子力学固有のものではありません。その背景には「状態変換の生成子」という普遍的な思考法があります。そして正準形式の古典力学の範疇だけでも、それはしっかり見てとれるのです。

古典力学の正準理論では、粒子の運動量pとその位置座標qの関数である物理量AとBに対して、ポアソン括弧というとても便利なものが定義されています。

エネルギーという物理量は、正準理論ではpとqの2変数の関数と見なされ、ハミルトニアンH(p,q)と呼ばれています。

これを使うと、系の基礎的な運動方程式となる正準方程式は、以下のように簡単に書けます。

ある時刻でpとqの値を決めて、この方程式を解くことによって、未来（と過去）のp(t)とq(t)が一意に定まるのです。

この古典力学でも物理量に対して演算子を考えることは、とても自然なのです。例えばエネルギーには、下記のハミルトニアン演算子という微分演算子を対応させられます。

すると先の正準運動方程式は簡単に下記のように書き換えられるのです。ただしこの右辺では、まずpやqを独立変数だと思って演算子の中の微分を計算し、その後で時間の関数であるp(t)とq(t)をpやqに代入しています。

エネルギーだけでなく、pとqの関数である任意の物理量A(p,q)に対しても、同様の演算子は下記のように定義できます。

例えば運動量演算子と位置座標演算子は、下記のようになっています。

また運動量演算子を定数倍して指数関数の肩に乗せると、その演算子は粒子の位置と運動量に関する確率分布関数ρ(p,q)に対して、下記のように位置座標の値に定数を加える作用を与えます。つまり運動量演算子は、古典力学でも位置座標の推進演算子なのです。同様に位置座標演算子から作られる演算子は、運動量の値に対する推進演算子になっています。このような変換の生成子として、位置演算子と運動量演算子は理解できます。

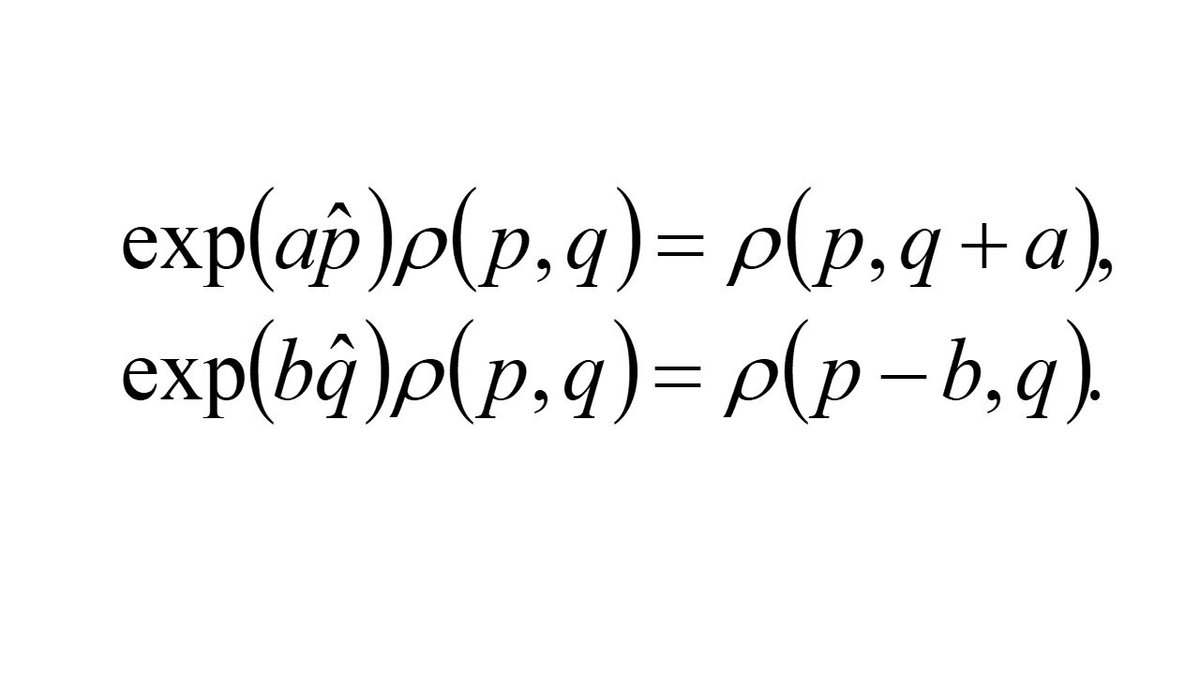
このように古典力学でも指数関数exp(・)を通じて、この物理量の演算子は状態変化を生み出す「生成子」であると理解できるのです。また状態変化の生成子という見方から、対称性に関する有名な「ネーターの定理」というものも証明できます。つまり対称性がある場合には、その生成子の物理量が時間的に変化しないという保存則が自動的に出てくるのです。演算子という表記を使えば、古典力学や量子力学、更にその２つとも異なる一般的な確率理論に対してさえも、この生成子と対称性の関係は普遍的な形で論じることが可能です。

量子力学を学ぶとき、しばしば物理量が「演算子」になるということが強調され過ぎて、学ぶ人はそこにある種の神秘性を感じてしまうかもしれません。でもここで述べたように、実はそれは古典力学でも普通に起きていることであり、特に不思議でも何でもないのです。

なおこのような枠組みから、量子力学を操作論的な情報理論として正しく扱う下記の教科書を書いております。ご参考にして頂ければ幸いです。