
【コンピュータの内側】第2回 「数理論理学の世界」
今回は、コンピュータの動作原理の基礎となっている、数理論理学に焦点を当てます。機械がどうやって計算を行うのか、その秘密はここに隠されています!
ただし、数理論理学がコンピュータでどのように利用されているかについては、次回以降に説明を持ち越そうと思います。少しモヤモヤするかもしれませんが、まずは基本的な部分から、確実にステップアップしていく形式を取りました。
是非、最後までお付き合いください。
論理学から数理論理学へ
論理学という言葉を聞いたことがあるでしょうか。
古代ギリシアやインドで発展した学問で、非常に古い歴史を持っているそうです。論理(Logic)の名の通り、物事について正しく認識するためにはどのような道筋で思考・論証すればよいのかを研究する分野です。
長らく「思考法」としての側面が強調されていた論理学ですが、数学との出会いによって「数理論理学」という新たな道へ発展しました。今回紹介するのは、数理論理学の中でも「命題論理」とよばれる分野です。
論理学とは、ある事柄について、前提条件から推論を導き出す手法であると言えます。前提条件や推論は「命題」と呼ばれる文章で記述されます。命題は、「正しい」か「間違い」かのどちらかの状態をとる文章でなくてはなりません。「正しいけれど間違っている」という状態はありえないものとみなされるのです。
命題が正しいことを「真」、間違っていることを「偽」と呼びます。
下の例を見てみましょう。
命題1:すべての哺乳類は生物である
命題2:人類は哺乳類である
→ ゆえに人類は生物である
2つの命題は明らかに真ですので、この推論は成り立ちます。しかし、次の場合はどうでしょう。
命題1:人類は生物である
命題2:人類は哺乳類である
→ ゆえにすべての哺乳類は生物である
これは成り立ちそうにありません。
より正確には、与えられた2つの命題からこの推論を導くことはできません。なぜならば、これらの命題の中では、すべての哺乳類が生物かどうかに関して言及していないためです。
これは、単なる言葉遊びではありません。一見複雑な事象も、このように単純化して考えることで確実に論証できるという、論理学の真髄です。
命題の記号化
数理論理学では、命題や推論を記号化して考えます。代数学的な手法によって、命題同士の本質的な関係を調べようとしたのです。
たとえば、下の命題を「A」と記号化します。
A:すべての哺乳類は生物である
さらに、命題の真偽をそれぞれ「1」「0」という数値で表します。このとき、命題の真偽を表す数値を「真理値」と呼びます。かっこいいですね。
以上に則ると、命題Aが真であることを「Aの真理値は1」、偽であることを「Aの真理値は0」と表せます。少しずつ数学感が出てきましたが、言っていることは何ら変わりありません。
命題同士の関係
次に、3つの命題の関係性を見てみましょう。
A:すべての哺乳類は生物である
B:人類は哺乳類である
C:人類は生物である
このとき、「AとBの真理値が1であれば、Cの真理値も1」という論理が成り立ちます。「すべての哺乳類が生物であり、かつ人類が哺乳類であるならば、人類は生物である」ということです。
言い換えれば、「AかつBならばC」。なんとなく、3つの命題同士の関係の本質を表していそうです。
ここで、新たな記号を紹介します。
∧:かつ (AND)(A∧B:AとBがともに真である場合のみ真となる)
∨:または(OR)(A∨B:AとBどちらか一方でも真であれば真となる)
¬:否定 (NOT)(¬A:A が偽の場合に真となる)
これらは論理記号と呼ばれます。数学の計算式で + - × ÷ が使われるように、数理論理学の論理式では ∧ ∨ ¬ が使用されるのです。(これ以外にも分野によって様々な記号があてがわれていますが、意味は同じです)
「AかつB」は、論理記号を使って次のように表せます。
A∧B
すごく数学感があります!
以下の表にまとめた通り、AとBの真偽の組み合わせは4通りあります。A∧Bが真となるのは、AとBがともに真の場合のみです。このように、ある論理式について考えられるすべての状態と結果を表す表を「真理値表」と呼びます。
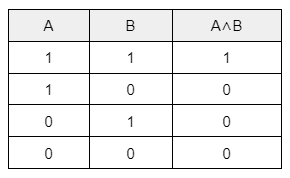
論理演算の主要な法則
さらに数学っぽいことを言いましょう。
論理式として命題を扱える最大の利点は、代数学のように式を変形できることにあります。たとえば、論理演算では四則演算と同様、交換法則、分配法則、結合法則が成り立ちます。
交換法則:A∧B = B∧A、A∨B = B∨A
分配法則:A∧(B∨C) = (A∧B)∨(A∧C)
A∨(B∧C) = (A∨B)∧(A∨C)
結合法則:(A∧B)∧C = A∧(B∧C)
(A∨B)∨C = A∨(B∨C)
また、二重否定、つまり否定の否定は元の命題に戻るという性質があります。さらに、これらの発展型として、ド・モルガンの法則という便利な法則がよく利用されます。
復元法則 (二重否定):¬(¬A)=A
ドモルガンの法則:¬(A∧B) = ¬A∨¬B
¬(A∨B) = ¬A∧¬B
ベン図
ドモルガンの法則のように複雑な式は、「ベン図」で表すと関係性がわかりやすくなり、便利です。早速試してみましょう。
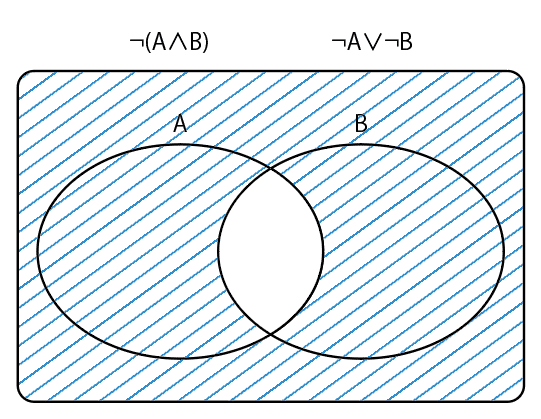
どうでしょうか。
¬(A∧B)とは、AかつB(AとBの円が重なった部分)以外の全てです。
¬A∨¬Bとは、A以外の全てまたはB以外の全て、どちらか1方でも該当する部分を指しており、両者は全く同義であることがわかります。
ベン図を用いることで、ドモルガンの法則が正しいことを簡単に示せるのです。
まとめ
今回は、コンピュータの動作原理の基礎である数理論理学について学びました。命題論理では、命題を記号化することで、代数学のように式を変形させながら命題同士の関係性を見ることができたと思います。
ところで、命題の真理値0、1と、コンピュータがデジタル信号で表現する0、1。いかにも親和性がありそうではないですか?
もしも、電子回路でAND、OR、NOTのような単純な論理演算を表現できたとして、さらに論理演算を使って四則演算を行えるとしたら、コンピュータが「計算」をするための仕組みとして利用できそうです。
ということで次回は、論理演算によって四則演算が可能かどうか検証していきましょう!
この記事が気に入ったらサポートをしてみませんか?
