【統計学】正規分布はサイコロ(の断面)〜二次関数と三次関数による正規分布の近似
要約
正規分布は、サイコロ(立方体・超立方体)を偏差平面($${x_1+x_2+ \cdots +x_n =k}$$)でスライスした時の断面上の格子点数の函数グラフとほぼ一致した。当然か。2回勝負より3回勝負の方がより一致したので間違いないと思われる。
両者は無限次元の超立方体で一致すると思われるが難しくて先送り。
発想
統計学の解説書等では「二項分布は極限で正規分布に一致し、その証明はスターリングの公式による」と大体書いてありますが、このスターリングの公式というのがゴリゴリの数式で感覚的に掴むのに骨が折れそうだし素人さんはこれを読んでもケムに巻かれるだけだろうな、何かないかなあ、と考えていました。
試しに、1-6のサイコロで(多分これは多項分布という奴だろうなと思いつつ)計算してみて、出目を大きくするか、サイコロを振る回数を増やせば正規分布に近づくのだろうと見当をつけて計算してみました。
サイコロ3回勝負
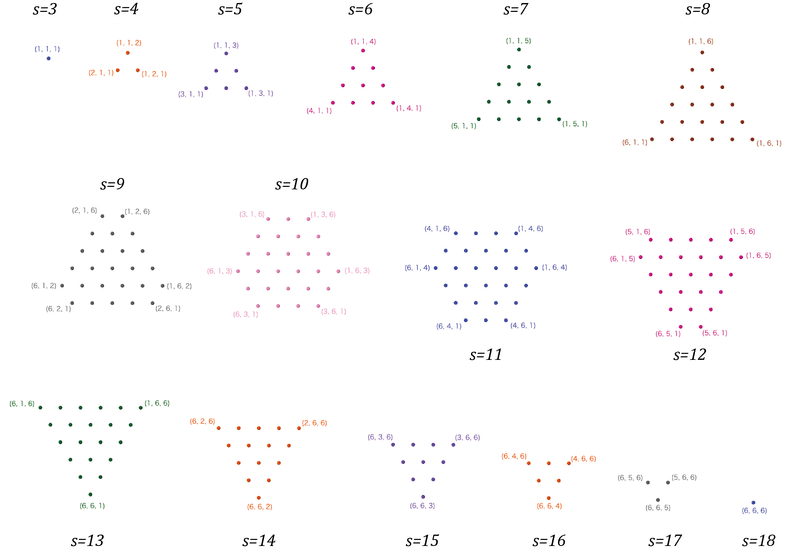
まずは、1~6全て出る確率は同じ(としないと面倒)として、サイコロを$${n=3}$$回振り、出目の合計$${s}$$の分布、つまりは組み合わせ数を気合いで調べてみます。
組み合わせ数え上げ
最小は$${1+1+1=3}$$、最大は$${6+6+6=18}$$ですね。組み合わせ総数は、$${6^3=216}$$にもなります。
多分、数値の組み合わせの右の方は隠れていると思いますのでスクロールして見て下さい。せっかく216通りも頑張って書いたので。
$$
\begin{align*}
s&=3 \quad & \Rightarrow 1 \qquad &111 \\
s&=4 \quad & \Rightarrow 3 \qquad &112 121 211\\
s&=5 \quad & \Rightarrow 6 \qquad &113 122 131 212 221 311\\
s&=6 \quad & \Rightarrow 10 \qquad &114 123 132 141 213 222 231 312 321 411 \\
s&=7 \quad & \Rightarrow 15 \qquad &115 124 133 142 151 214 223 232 241 313 322 331 412 421 511\\
s&=8 \quad & \Rightarrow 21 \qquad &116 125 134 143 152 161 215 224 233 242 251 314 323 332 341 413 422 431 512 521 611\\
s&=9 \quad & \Rightarrow 25 \qquad &126 135 144 153 162 216 225 234 243 252 261 315 324 333 342 351 414 423 432 441 513 522 531 612 621\\
s&=10 \quad & \Rightarrow 27 \qquad &136 145 154 163 226 235 244 253 262 316 325 334 343 352 361 415 424 433 442 451 514 523 532 541 613 622 631\\
s&=11 \quad & \Rightarrow 27 \qquad &146 155 164 236 245 254 263 326 335 344 353 362 416 425 434 443 452 461 515 524 533 542 551 614 623 632 641\\
s&=12 \quad & \Rightarrow 25 \qquad &156 165 246 255 264 336 345 354 363 426 435 444 453 462 516 525 534 543 552 561 615 624 633 642 651\\
s&=13 \quad & \Rightarrow 21 \qquad &166 256 265 346 355 364 436 445 454 463 526 535 544 553 562 616 625 634 643 652 661\\
s&=14 \quad & \Rightarrow 15 \qquad &266 356 365 446 455 464 536 545 554 563 626 635 644 653 662\\
s&=15 \quad & \Rightarrow 10 \qquad &366 456 465 546 555 564 636 645 654 663\\
s&=16 \quad & \Rightarrow 6 \qquad &466 556 565 646 655 664\\
s&=17 \quad & \Rightarrow 3 \qquad &566 656 665\\
s&=18 \quad & \Rightarrow 1 \qquad &666\\
\end{align*}
$$
あれ?$${s=3}$$から$${s=8}$$までの組み合わせ数、$${1,3,6,10,15,21}$$という数の並びは、どこかで見たことが…
あれですね。高校数学でもお馴染みの、$${1+2+3+ \cdots +n}$$の式
$$
\sum_{k=1}^{n}k =\dfrac{1}{2}n(n+1)\\
$$
です。$${s=9}$$から$${s=10}$$までは増加するが$${27}$$で頭打ち、$${s=11}$$の同じ$${27}$$から折り返して逆の経過を辿って$${666}$$で完結、となっています。これはどういうことだろう。
組み合わせの構造
上の出目の組み合わせ$${(111,323)}$$等を3次元の座標に落とし込んで構造を見て見ましょうか。

ごちゃごちゃしているように見えますが、当然、この立方体の中に、綺麗に格子状に並んでいます。このような整数だけの点を格子点と呼びます。
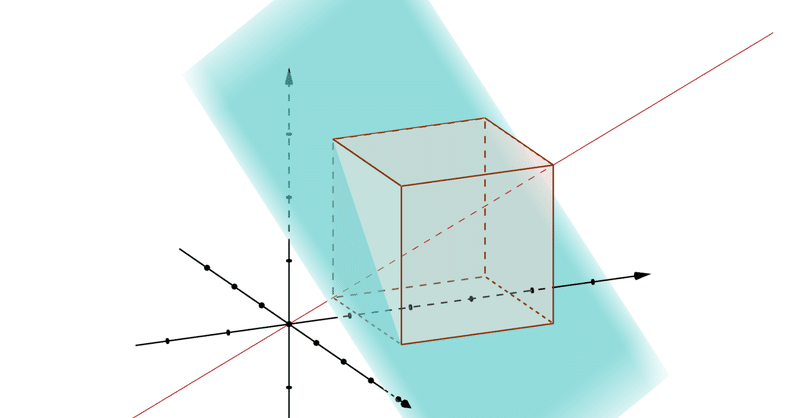
ここで、同じ出目の合計$${s}$$となる点は、この立方体をこんな風に斜めの面で切り取った上に並びます。この面を「偏差平面」と仮に呼びましょう(分散や偏差ベクトルは必ずこの面上で展開するから)。
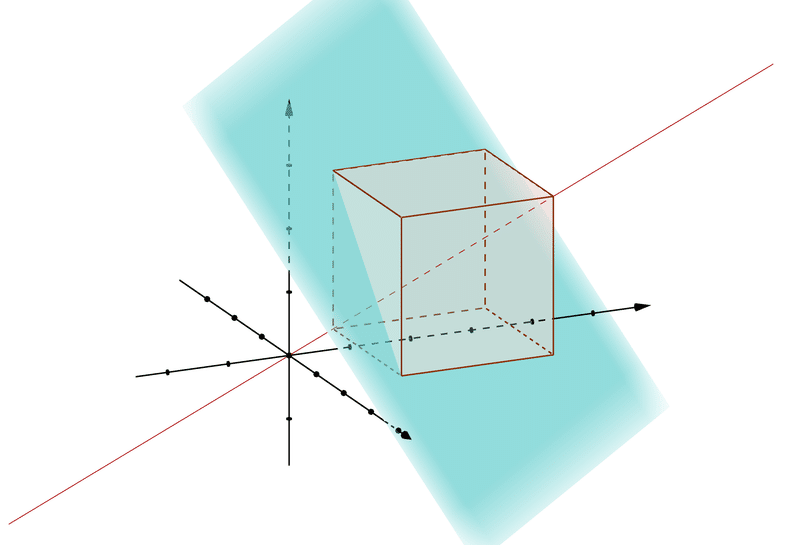
この偏差平面は、普通の方程式で書くと$${x+y+z=s}$$となります。合計が$${s}$$となる点がこの上にあるのは当然ですね。
また、この偏差平面は$${s}$$の値に関わらず常に直線$${x=y=z}$$に垂直です。この直線を「平均値直線」と呼びます。「ゾロ目直線」でもいいかも知れません。この直線上の点は全て$${(1,1,1) (4,4,4)}$$のようにゾロ目になるからです。偏差平面と平均値直線が常に垂直であるのは平面の方程式の定義や内積で簡単に示せます。
中を覗くと、こんな感じです。今度は偏差平面$${s=6}$$で切って見ました。
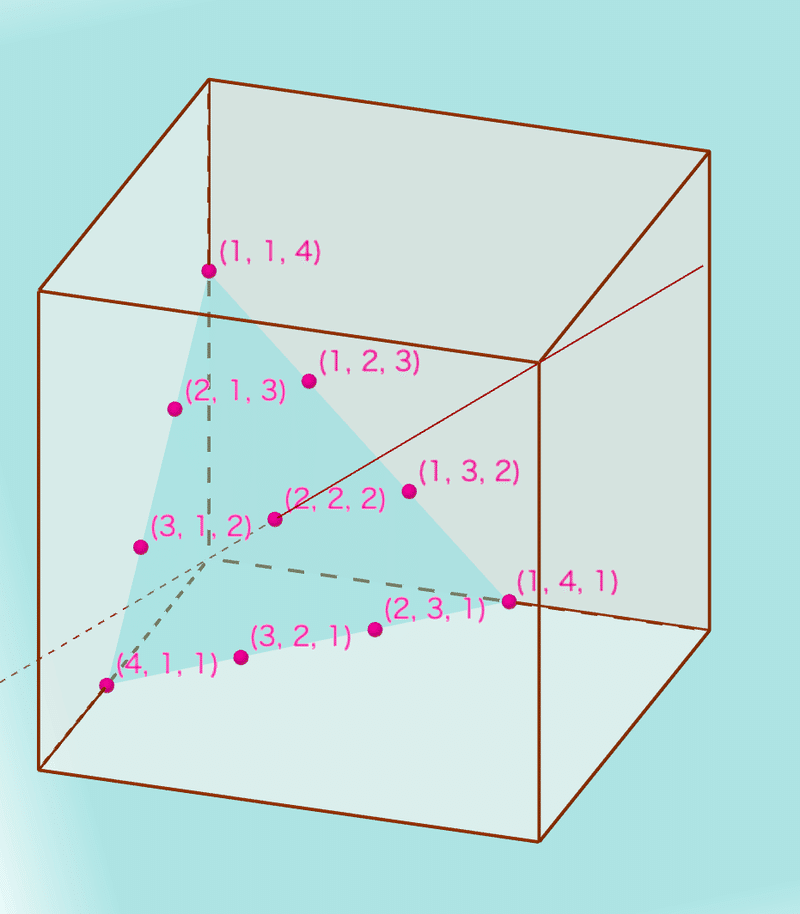
ここでは明らかに切断面は正三角形ですね。$${s=8}$$まで正三角形になりそうですが、それ以降は三角形の角が取れます。出目が6までなので、$${(1,1,7)}$$のようなあり得ない点が削れていく感じです。確認しましょう。今度は平均値直線方向から垂直に切断面を見ます。
結局、予想通り、$${s=9}$$からは、3つの角からはみ出た分を削いでいくことになります。
格子点函数でグラフを描画
さて、格子点数を、出目の合計$${s}$$の函数$${L_i(s)}$$とすると、こう書けば辻褄が合います。
$$
\begin{align*}
L_1(s)&=\dfrac{1}{2}(s-2)(s-1) , &\quad 3\leq s \leq 8\\
L_2(s)&=\dfrac{1}{2}(s-2)(s-1)-3 \cdot \dfrac{1}{2}(8-s)(7-s) , &\quad 9\leq s \leq 12\\
L_3(s)&=\dfrac{1}{2}(20-s)(19-s) , &\quad 13\leq s \leq 18\\
\end{align*}
$$
$${L_2(s)}$$の右辺第2項$${-3 \cdot \dfrac{1}{2}(8-s)(7-s)}$$で、3つの角から正三角形を取り除いています。
ここで考察。
仮に、出目が1~12のサイコロで同じことをしても、単に立方体が2倍の大きさ(体積は8倍)になるだけで構造は同じ、やはり13を超えると角から正三角形を取り除くだけである。つまり、数字が大きくなるだけである。
これは、サイコロの出目を0.5, 1, 1.5, … 5.5, 6.0 として同じ大きさの立方体の中に2倍の格子点を詰め込んでも同じことになる。出目をもっと細かく0.1とか0.0001とかにしても本質的には同じこと。
ならば、この格子点函数は離散的(飛び飛びの値をとる)ではあるが、限りなく細かい出目を設定すれば、限りなく格子点がぎゅうぎゅうに詰まり、しまいには連続関数と見做しても良いのではないか。
その厳密な証明は保留して、とりあえずグラフを描いて確認してみましょう。
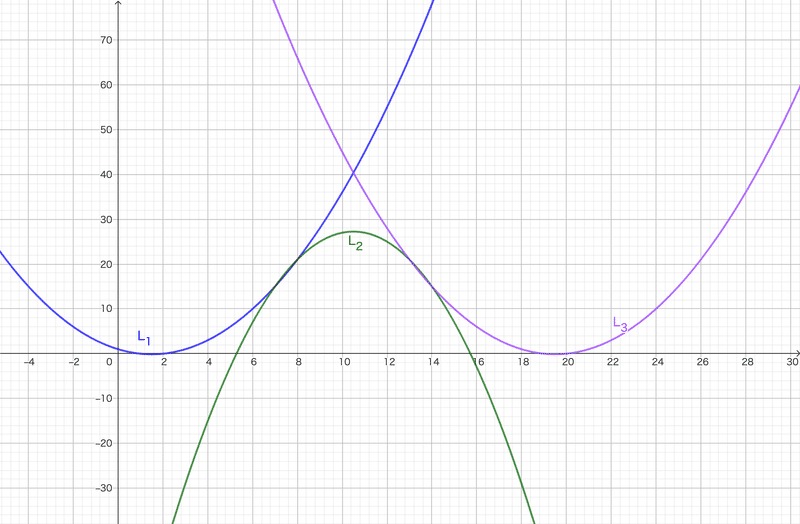
$${L_1(s)}$$は、$${s=8}$$で$${L_2(s)}$$に、$${L_2(s)}$$は、$${s=13}$$で$${L_3(s)}$$にバトンタッチします。
正規分布との比較
ここで、今回の出目の平均$${\mu }$$と分散$${\sigma^2}$$は(算出は略)、$${\mu =10.5, \sigma^2=8.75}$$なので、正規分布は
$${ N(10.5, 9.716)=\dfrac{1}{2 \cdot \pi (8.75)^2} exp\left( -\dfrac{(x-10.5)^2}{2 \cdot (8.75)^2} \right)}$$
格子点函数$${L(s)}$$は規格化されておらず、このままでは比較できないので、$${L(s)}$$を(正の値の内側範囲である)2から19まで積分して面積を出します(詳細は略。まあまあ面倒くさい)。
$${\int _2^8 L_1(s)ds +\int _8^{13} L_2(s)ds + \int _{13}^{18} L_3(s)ds =216.5}$$
最終的に、比較のために上の面積を正規分布に掛けた函数$${G(s)}$$を用意して、重ねて描画してみましょう。
$${ G(s)=216.5 \cdot N(10.5, 9.716)=\dfrac{216.5}{2 \cdot \pi (8.75)^2} exp\left( -\dfrac{(x-10.5)^2}{2 \cdot (8.75)^2} \right)}$$
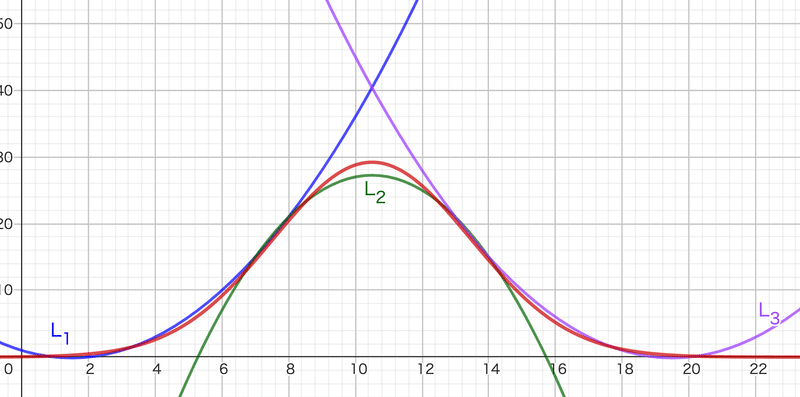
赤い線が、面積合わせ正規分布$${G(s)}$$のグラフです。
いかがでしょう。文字通り、結構いい線ではないでしょうか?
サイコロ4回勝負
四次元の世界へ
人間、こうなれば欲が出るもので、サイコロ4回勝負で勝負してみたくなりますよね。もっといい線を出してガッツポーズ出したいですよね。
しかし今回は、流石に3回勝負の時のように全部書き出すのは余りに面倒くさい。類推からなんとかならないか。
今回扱うのは、4次元超立方体。頂点は16。全ての格子点の座標は書けるが人類に絵は描けない。
但し、4次元超立方体の断面は我らが3次元の正四面体になるはず。なぜなら、原点に一番近い角の座標は$${(1,1,1,1)}$$、$${s=4}$$、次の(超)断面$${x+y+z+w=s: s=5}$$は、$${(1,1,1,2)(1,1,2,1)(1,2,1,1)(2,1,1,1)}$$の4つの頂点を持つからです。
尚、このままでは絵は描けませんが、この(超)断面上の点は$${x+y+z+w=5}$$という三次元断面に拘束されており(3次元の断面$${x+y+z=5}$$上の点$${x,y,z}$$が平面上に拘束されているのと同様)、正四面体であることは明らかです。
立式
さて、結論からいうと、今回の式は以下のようになります。格子点的には$${4 \leq s \leq 24}$$ですが、連続函数とした場合に正となる$${3 \leq s \leq 25}$$で定義します。
$$
\begin{align*}
L_1(s)&=\dfrac{1}{6}(s-3)(s-2)(s-1) , &\quad 3\leq s \leq 9\\
L_2(s)&=\dfrac{1}{6}(s-3)(s-2)(s-1)-4 \cdot \dfrac{1}{6}(s-9)(s-8)(s-7) , &\quad 9\leq s \leq 14\\
L_3(s)&=\dfrac{1}{6}(27-s)(26-s)(25-s)-4 \cdot \dfrac{1}{6}(19-s)(18-s)(17-s) , &\quad 14\leq s \leq 19\\
L_4(s)&=\dfrac{1}{6}(27-s)(26-s)(25-s) , &\quad 19\leq s \leq 25\\
\end{align*}
$$
要領は3回勝負の時と同じ。変わり目が9,14,19なので、そのタイミングで正四面体の個数をさっ引くことになります。
実は4回勝負の$${L_1(s)}$$は、kの和の式の和、
$$
\sum_{l=1}^n \sum_{k=1}^{l}k =\sum_{l=1}^n \dfrac{1}{2}l(l+1)=\dfrac{1}{12} n(n+1)(2n+1)+\dfrac{1}{4}n(n+1)=\dfrac{1}{6}n(n+1)(n+2)\\
$$
と同じものです。また、これは組み合わせ$${_n C_3}$$そのものでもあります。今回登場する式は、色々な解釈が可能ですが本論から外れるのでここまで。
正規分布との比較
さて、3次元の時と同じく面積を出すと(今回は積分マシンのお世話になりました)、
$${\int _2^9 L_1(s)ds +\int _9^{14} L_2(s)ds + \int _{14}^{19} L_3(s)ds+ \int _{19}^{25} L_4(s)ds =1295.75}$$
ここで、今回の出目の平均$${\mu=14 }$$と分散$${\sigma^2}$$は(算出は略)、$${\mu =10.5, \sigma^2=12.5}$$なので、面積合わせ正規分布$${G(s)}$$は、
$${ G(s)=1295.75 \cdot N(14, 12.5)=\dfrac{1295.7}{2 \cdot \pi (12.5)^2} exp\left( -\dfrac{(x-14)^2}{2 \cdot (12.5)^2} \right)}$$
さて描画して見ましょう。まず$${L(s)}$$のみ。
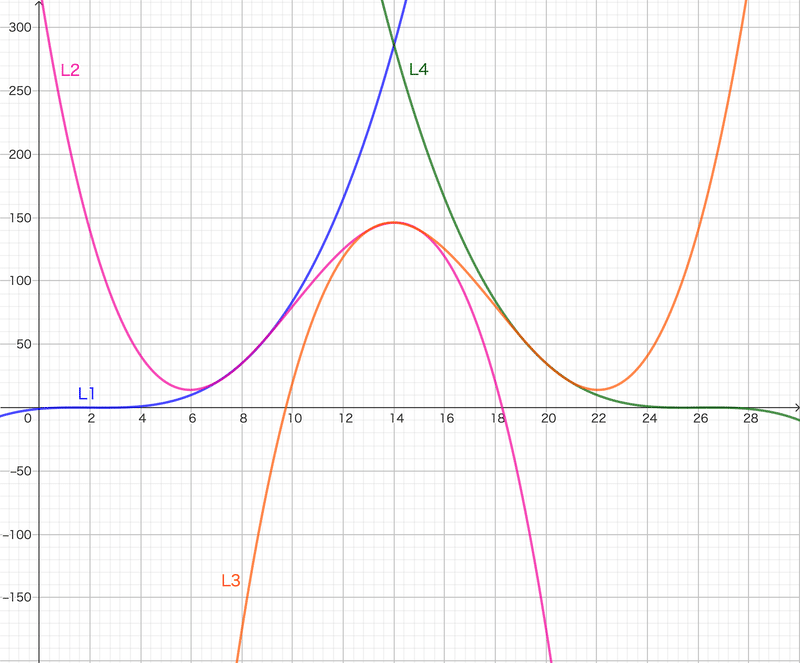
では、面積合わせ正規分布$${G(s)}$$を重ねます。

正規分布$${G(s)}$$の赤い線が重なりすぎてほぼ分かりません。
拡大してみましょう。

いかがでしょうか。
結論
正規分布は(少し気合いの入った)サイコロの斜めスライス断面である。
考察
サイコロ回数(次元数)だけ式は分割され、その幅はどうも5(両端は少し広いが)らしいです。要するに一辺の長さですね。
2次元もやって見ましたが、またの機会に(追記するかも知れません)。
更に一般化して、n次元での$${L(s)}$$を統一的に書いて、$${n \rightarrow \infty}$$で合体して正規分布の式に飛ばないかなあ、無理かなあ。
まあとりあえずこの辺で。
この記事が気に入ったらサポートをしてみませんか?
