
統計準1級 第6章 連続型分布と標本分布 解説
連続型分布
連続型確率分布はストーリーを考えながら理解すると早い
離散型連続型で頻出の確率分布は下記の記事にまとめられているので適宜参考にされたい
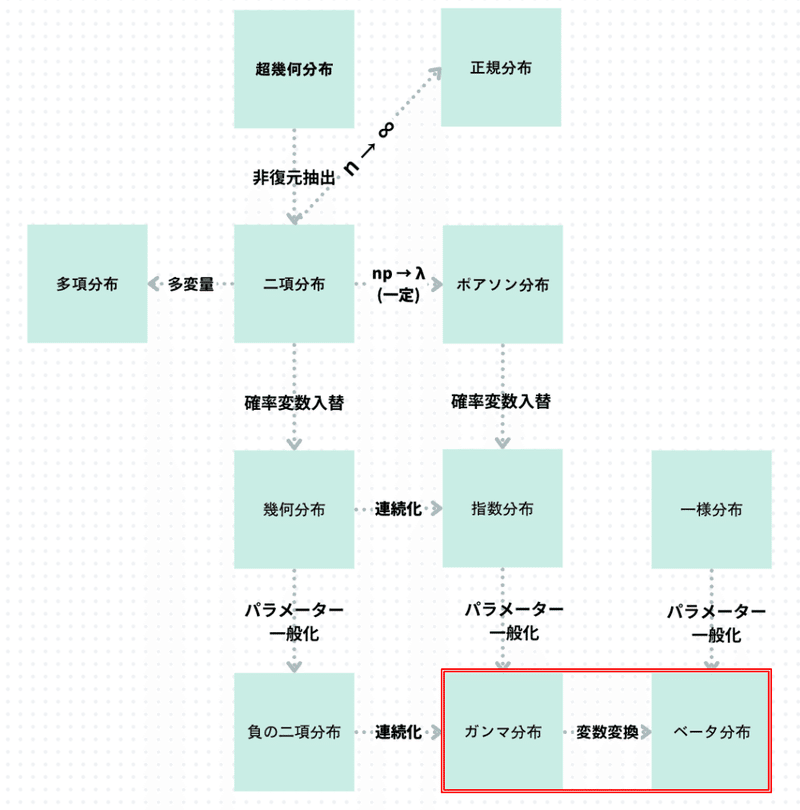
今回取り上げる連続型確率分布は下図の赤線部分である

正規分布

正規分布は
二項分布の試行回数$${n}$$が大きく
$${np >> 1}$$のように期待値が1より十分大きい時に
近似できる分布
$$
\begin{aligned}
& f(x) = \frac{1}{\sqrt{2\pi}\sigma}exp\bigg\lbrace-\frac{1}{2}\bigg(\frac{x - \mu}{\sigma}\bigg)^2\bigg\rbrace
\end{aligned}
$$
確率変数 : 成功回数 $${X}$$
パラメーター : 平均値$${\mu}$$ 分散$${\sigma}^2$$
分布の証明は下記を参照
https://www.eee.kagoshima-u.ac.jp/~watanabe-lab/misc/%E4%BA%8C%E9%A0%85%E5%88%86%E5%B8%83.pdf
2変量正規分布
2変量正規分布の
条件付き期待値の条件付き期待値と分散は下記のようになる
期待値は元々の期待値に2変数の相関と$${X}$$自体の影響で値が変化し
分散は元々の分散に2変数の相関の影響で値が少し小さくなる

詳しい証明は下記を参照
指数分布

二項分布と幾何分布の対応と同様に
ポアソン分布と指数分布も確率変数の入れ替えをしている
ポアソン分布は時間を固定した成功回数の確率分布である一方で
指数分布は成功回数を固定した時間の確率分布となっている
確率変数 : (r回成功するまでの)時間 $${X}$$
パラメーター : 平均値、分散$${\lambda}$$
$$
\begin{aligned}
& f(x) = \lambda e ^{-\lambda x}
\end{aligned}
$$
証明は下記を参考
ガンマ分布

ガンマは超ウルトラ簡単で
確率変数の制約条件を
(1回成功するまでの)→ (r回成功するまでの)
に一般化するだけである
確率変数 : (r回成功するまでの)時間 $${X}$$
パラメーター : 平均値、分散$${\lambda}$$ $${\alpha}$$, $${\beta}$$
$$
\begin{aligned}
& f(x) =\frac{1}{\Gamma(\alpha)} \frac{1}{\beta} \bigg(\frac{x}{\beta}\bigg)^{\alpha-1} e^{- \frac{x}{\beta}}
\end{aligned}
$$
ベータ分布
ベータ分布はガンマ分布を変数変換したもの
$$
B(\alpha,\beta) = \frac{\Gamma(\alpha) \Gamma(\beta)}{\Gamma(\alpha + \beta)}
$$
証明は下記を参考にされたい
https://academ-aid.com/statistics/gamma-beta
また性質を一言で表現すると
ベルヌーイ試行において
成功回数と失敗回数がわかっている時の成功回数の分布
この成功回数と失敗回数が事前にわかっている状態が
ベイズ統計でいう事前分布に導入できるので
ベイズ統計学でよく使われる分布になっている
確率変数 : 成功する確率$${p}$$
パラメーター : 成功回数 $${\alpha}$$, 失敗回数 $${\beta}$$
$$
\begin{aligned}
& P(p = x) \\{}\\& = B(\alpha,\beta) \\{}\\
& = \frac{x^{\alpha-1} (1-x)^{\beta-1}} {B(\alpha,\beta)}
\end{aligned}
$$
標本分布
母平均や母分散みたいな母集団のパラメーター推測の際に
標本平均、標本分散みたいな統計量の分布を知ることが必要
このときの統計量の分布を標本分布という
標本分布は主に
$${\chi^2}$$分布
$${t}$$分布
$${F}$$分布
がある
カイ二乗分布

・ $${\chi^2_n}$$分布は標準正規分布の2乗和
この$${\chi^2_n}$$分布は
$${X_1, X_2, \cdots, X_n}$$が独立で、確率変数が標準正規分布に従うとき$${X_i 〜 N(0,1)}$$の2乗和$${\chi^2_n = X^2_1, X^2_2, \cdots, X^2_n}$$
が従う分布としても知られている
・ $${\chi^2_n}$$分布はガンマ分布の特殊系
また、$${\chi^2_n}$$分布とはガンマ分布の特殊な形でできている
$$
\begin{aligned}
& f(x) =\frac{1}{\Gamma(\alpha)} \frac{1}{\beta} \bigg(\frac{x}{\beta}\bigg)^{\alpha-1} e^{- \frac{x}{\beta}}
\end{aligned}
$$
のガンマ分布において$${\alpha = \frac{n}{2}, \beta = 2}$$とすると
$$
\begin{aligned}
& f(x) =\frac{1}{\Gamma(\frac{n}{2})} \bigg(\frac{1}{2}\bigg)^{\frac{n}{2}}x^{\frac{n}{2}-1} e^{- \frac{x}{2}}
\end{aligned}
$$
これが$${\chi^2_n}$$分布となる
・ $${\chi^2_n}$$分布の平均と分散
$${\chi^2_n}$$分布の平均は$${n}$$,分散は$${2n}$$となる
以下簡単に証明していく
まずモーメント母関数を求める
ガンマ分布の積分値が1になるのを利用すると
$$
\begin{aligned}
M_x(t) &= \int e^{tx} \times \frac{1}{\Gamma(\frac{n}{2})} \big(\frac{1}{2}\big)^{\frac{n}{2}}x^{\frac{n}{2}-1} e^{- \frac{x}{2}} \\{}\\
&= \int \frac{x^{\frac{n}{2}-1} e^{- \big(\frac{1 -2t}{2}\big)^x} }{\Gamma(\frac{n}{2})(1 - 2t)^{\frac{n}{2}}(\frac{2}{1 - 2t})^{\frac{n}{2}}} \\{}\\
&= (1 - 2t)^{- \frac{n}{2}} \int \frac{x^{\frac{n}{2}-1} e^{- \big(\frac{1 -2t}{2}\big)^x} }{\Gamma(\frac{n}{2})(\frac{2}{1 - 2t})^{\frac{n}{2}}} \\{}\\
&= \bigg(\frac{1 }{1 - 2t}\bigg)^{\frac{n}{2}} (\because \int \frac{x^{\frac{n}{2}-1} e^{- \big(\frac{1 -2t}{2}\big)^x} }{\Gamma(\frac{n}{2})(\frac{2}{1 - 2t})^{\frac{n}{2}}} = \int Gamma\bigg(\frac{n}{2} , \frac{2}{1 - 2t} \bigg) = 1 )\\{}\\
\end{aligned}
$$
平均 :
求めるのは$${E(\chi^2_n) = M'_x(0)}$$である
$$
\begin{aligned}
M'_x(t) &= \frac{n}{2} \bigg(\frac{1}{1 - 2t}\bigg)^{\frac{n}{2} - 1} \frac{2}{(1 - 2t)^2}
\\{}\\ & = n \bigg( \frac{1}{1 -2t} \bigg)^{\frac{n}{2} + 1}
\end{aligned}
$$
より$${M'_x(0) =n}$$となる
分散 :
求めるのは$${V(\chi^2_n) = M''_x(0) - (M'_x(0))^2}$$である
まずは$${M''_x(0)}$$を求める
$$
\begin{aligned}
M'_x(t) &= n \bigg(\frac{n}{2}+1\bigg) \bigg(\frac{1}{1 - 2t}\bigg)^{\frac{n}{2} - 1 +1} \frac{2}{(1 - 2t)^2}
\\{}\\ & = 2n \bigg(\frac{n+2}{2}\bigg)\bigg( \frac{1}{1 -2t} \bigg)^{\frac{n}{2} + 2}
\\{}\\ & = n (n+2)\bigg( \frac{1}{1 -2t} \bigg)^{\frac{n}{2} + 2}
\end{aligned}
$$
より$${M''_x(0) = n (n+2)}$$となる
従って
$$V(\chi^2_n) = M''_x(0) - (M'_x(0))^2 = 2n$$
t分布

・ t分布は標準正規分布と$${\chi^2_n}$$分布の比
$${X, Y}$$が独立で、
確率変数$${X}$$が標準正規分布に従い$${X 〜 N(0,1)}$$
確率変数$${Y}$$が標準正規分布に従い$${Y 〜 \chi^2_n}$$のとき
$$
T = \frac{X}{\sqrt{\frac{Y}{n}}}
$$
は$${t}$$分布に従う
この関係式の導出は下記を参照
・ t分布の平均と分散
$${t}$$分布の平均は$${0}$$,分散は$${\frac{n}{n-2}}$$となる
平均と分散についての導出は統計検定準1級の範囲を超えているのでここでは紹介しない
気になる方はこちらの記事にまとまっているので参照されたい
F分布

・ F分布は$${\chi^2_n}$$分布の比
F分布は$${\chi^2_n}$$分布の比で知られている
$$
\begin{aligned}
F_{(m,n)} &= \frac{\frac{\chi^2_m}{m}}{ \frac{\chi^2_n}{n}} \\{}\\
&= \frac{\frac{\sum_m (X_m - \mu)^2}{m}}{ \frac{\sum_n (X_n - \nu)^2}{n}}
\end{aligned}
$$
・ F分布の平均と分散
F分布の平均は$${\frac{n}{n - 2}}$$,分散は$${2(\frac{n}{n - 2})^2 \frac{n + m - 2}{m(n - 4)}}$$となる
平均と分散についての導出は統計検定準1級の範囲を超えているのでここでは紹介しない
気になる方はこちらの記事にまとまっているので参照されたい
この記事が気に入ったらサポートをしてみませんか?
