
統計準1級 第5章 離散型分布 解説
統計検定準1級に出てくる
確率分布を下記のような関連図を用いて
ストーリー立てて解説する

確率分布の関係性が解説されているサイトが
あまりなくストーリー重視ですので、
確率分布の証明は省略しています
また自分の備忘録も兼ねているので、
少し雑になっている部分はごめんなさいっ
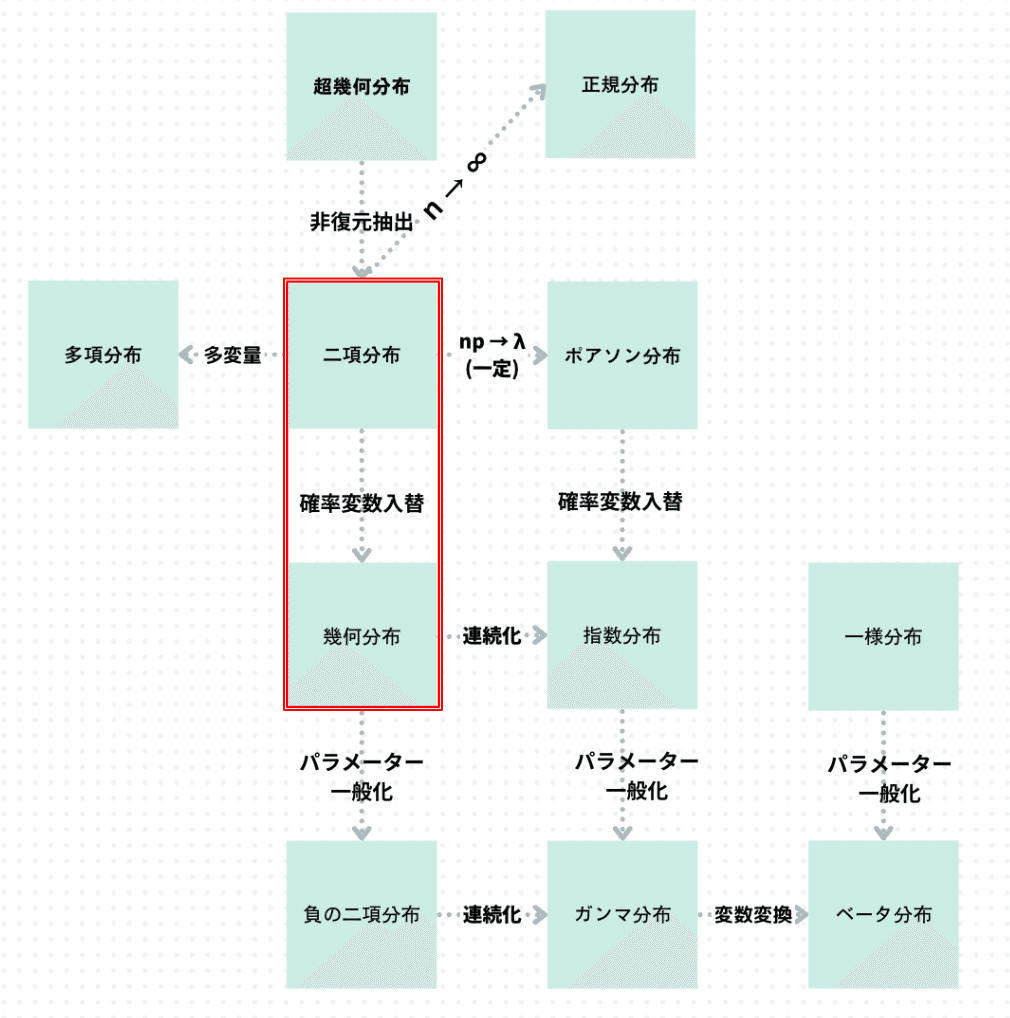
二項分布

ここが全ての始まりであり、後から出てくる様々な確率分布の基礎
二項分布とは
ベルヌーイ試行(事象が表裏みたいに2通り)を独立に$${n}$$回行って
成功する回数を確率変数$${X}$$とした時に従う確率分布
確率変数 : 成功回数 $${X}$$
パラメーター : 成功する確率$${p}$$
$$
\begin{aligned}
& P(X = k) = {}_{n} C_{k} p^k (1-p)^{n-k}
\end{aligned}
$$
超幾何分布

二項分布と超幾何分布の違いはたったこれだけ
二項分布 -> すべての試行の確率は同じ
超幾何分布 -> 試行ごとに次の試行の確率が変化
この違いは下記の例で考えたらわかりやすい
例えば
赤玉4個白玉6個の合計10個あって
合計4個取り出して赤玉3個取り出したいとする
二項分布のときは
1回玉を取り出したら戻す、それを4回
超幾何分布のときは
1回玉を取り出したら戻さない、それを4回
つまり超幾何分布とは
有限の$${N}$$個の要素がある母集団から
$${n}$$個要素を取り出した時に$${k}$$個の成功事象が含まれる確率分布
確率変数 : $${k}$$回の抽出で得られた成功事象を持つ要素数 $${X}$$
パラメーター : 全体の有限母集団数$${N}$$, 成功事象を持つ母集団要素数$${M}$$, 試行で抽出される要素数$${n}$$
$$
\begin{aligned}
& P(X = k) = \frac{{}_{M} C_{k} × {}_{N - M} C_{n - k} }{{}_{N} C_{n}}
\end{aligned}
$$
超幾何分布について詳しくは下記を参照
多項分布

二項分布の多変量版が多項分布
二項分布は事象が2通りしかないベルヌーイ試行を$${n}$$回したものだったが
多項分布は事象が3通り以上(サイコロの出る目とか)ある試行を$${n}$$回した確率分布である
確率変数 : 事象が起きる回数 $${X_1, X_2, \cdots, X_k}$$
パラメーター : 事象が起きる確率 $${p_1, p_2, \cdots, p_k}$$
$$
\begin{aligned}
& P(X_1 = x_1, X_2 = x_2, \cdots, X_k = x_k) \\
& = \frac{x!}{x_1! x_2! \cdots x_k!} p_1^{x_1} p_2^{x_2} \cdots p_k^{x_k}
\end{aligned}
$$
特に$${k=2}$$の時事象の種類が2通りなので
二項分布になることにも注意(当たり前)
$$
\begin{aligned}
& P(X_1 = x_1, X_2 = x_2) \\
& = \frac{x!}{x_1! x_2!} p_1^{x_1} p_2^{x_2} \\
& = \frac{x!}{x_1! (x - x_1)!} p_1^{x_1} (1- p_1)^{x - x_1} \\
& = {}_{x} C_{x_1} p_1^{x_1} (1-p_1)^{x-x_1}
\end{aligned}
$$
※ $${p_1 + p_2 = 1, x_1 + x_2 = x}$$を利用
ポアソン分布

ポアソン分布は
正規分布の$${n \rightarrow \infty}$$の制約条件に加え
$${p \rightarrow 0}$$、$${np = \lamda(定数)}$$
になる時の確率分布
このとき$${p}$$に着目すると
独立な試行をn回行った時に一定時間で
成功確率が$${p = \frac{\lambda(定数)}{n}}$$となっている
ここでは平均と分散は同じ値になるので
パラメーターは正規分布とは違い1種類
確率変数 :一定時間あたりの成功回数 $${X}$$
パラメーター : 平均値、分散$${\lambda}$$
$$
\begin{aligned}
& P(X = k) = \frac{\lambda^k}{k !}exp( -\lambda )
\end{aligned}
$$
証明は下記を参考
幾何分布
超幾何分布は二項分布と比べると
固定しているものと確率変数を入れ替えるだけであった
二項分布 -> すべての試行の確率は同じ
超幾何分布 -> 試行ごとに次の試行の確率が変化
二項分布と幾何分布の対応も似たようなもので
固定しているものと確率変数を入れ替えるだけである
具体的には、確率変数が
単位試行回数あたりの平均成功回数なのか
単位成功回数あたりの平均試行回数なのか
二項分布 -> 成功回数の確率分布 (試行回数は固定)
幾何分布 -> 試行回数の確率分布 (成功回数は固定)
確率変数 : (1回成功するまでの)試行回数 $${X}$$
パラメーター : 成功する確率$${p}$$
$$
\begin{aligned}
& = {}_{k-1} C_{r-1} p^{r} (1-p)^{k - r} \\
& = {}_{k-1} C_{1-1} p^{1} (1-p)^{k - r} \\
& = p (1-p)^{k - 1}
\end{aligned}
$$
負の二項分布

負の二項分布は超ウルトラ簡単で
確率変数の制約条件を
(1回成功するまでの)→ (r回成功するまでの)
に一般化するだけである
確率変数 : (r回成功するまでの)試行回数 $${X}$$
パラメーター : 成功する確率$${p}$$
$$
\begin{aligned}
& P(X = k) \\
& (k-1回の試行で 合計r-1回成功している確率) ×(k回目の試行で成功している確率) \\
& = {}_{k-1} C_{r-1} p^{r-1} (1-p)^{(k-1) - (r - 1)} × p \\
& = {}_{k-1} C_{r-1} p^{r} (1-p)^{k - r}
\end{aligned}
$$
この記事が気に入ったらサポートをしてみませんか?
