
細胞に表現型が現れる割合を検定したい
表現型が出るか否かを三回実験するとき、実験ごとにいくつの細胞をカウントすればいいのか、また何の検定がふさわしいのか。
初歩的なことも含めて学んだことを書いていきます。もし間違っていたらご指摘いただけると幸いです。
・導入

「細胞に対して、遺伝子Aの発現を抑制する実験を3回行い、核が大きくなっていた表現型の割合は40%、40%、20%の平均33%でした。一方のコントロールでは0%、0%、20%の平均6.6%でした。ExcelでT検定したらP値が0.047だったので、有意差があると結論づけます。」
「なるほどね。ずいぶんとキリが良い数字だけれど、毎回の実験では細胞を何個ずつ計測したの?」
「毎回の実験では、細胞は5個ずつカウントしました!」
「5個しかしてないの!?」
「はい、何がだめなんですか?」
細胞のカウント数として5個が少なすぎることは、直感的にわかります。細胞のカウント数は、一般的には最低30細胞、推奨50細胞といった相場がありますので。
では、なぜ30細胞なのでしょうか?5細胞はなぜ不適切なのでしょうか?
・T検定とT分布
カウントする細胞数を考えるうえで後々重要になるので、まず検定方法について書いていきます。
二群間で表現型の割合を比較するのなら、第一選択肢としてはT検定が考えられます。
T検定とは、Wikipediaによると…
t検定(ティーけんてい)とは、帰無仮説が正しいと仮定した場合に、統計量がt分布に従うことを利用する統計学的検定法の総称である。母集団が正規分布に従うと仮定するパラメトリック検定法であり、(以下略)
統計量Tは、二群のデータを与えたときに、平均値とか分散とかをこねくり回して得られる値です。詳細は難しいですしWikipediaを見てください。二群の平均値に有意差がない場合の統計量Tは以下のT分布に従って分布します。

vは自由度で、二群のデータ数をm,nとしたとき、v = m + n - 2になります。今回の場合のm, nは何回実験を繰り返したか、になるのでm = n = 3 と考えられます。
二群のデータから統計量Tを計算し、その値が例えば T=2 だった時、本当は平均値に差がないのに偶然 T >= 2になってしまう確率(T>=2の部分の面積)がP値です。両側分布なら|T| >= 2です。
大抵は有意水準α=0.05として、P<0.05なら有意差あり、と結論づけることになります。P=0.05だからと言って、5%の可能性で有意差がないという意味ではありません。
・正規分布に従う母集団
ではもう一度T検定とは、Wikipediaによると…
t検定(ティーけんてい)とは、帰無仮説が正しいと仮定した場合に、統計量がt分布に従うことを利用する統計学的検定法の総称である。母集団が正規分布に従うと仮定するパラメトリック検定法であり、(以下略)
T検定を使うための条件が、母集団が正規分布に従うことです。表現型の出現率である「40%、40%、20%」「0%、0%、20%」の母集団が、正規分布に従うことが、必要というわけです。
とりあえず「正規分布に従う 検定」で調べると、コルモゴロフ–スミルノフ検定(KS検定)などがヒットします。が、割合の比較にKS検定は必要ありません。
・割合の母集団を可視化する
まずは簡単のために一実験あたりたった2個の細胞をカウントすることにして、核が大きくなる表現型の真の確率は0.5である、ということにします。この実験を大量に行ったときに、判断された割合の分布が、母集団にあたります。
観察した2個の細胞の両方ともが大きな核を持っており、表現型の割合が「100%(1.0)」と判断される頻度は、
0.5 * 0.5 = 0.25
となります。同様に、細胞の核が両方とも小さく、割合「0%」と判断される頻度も0.25、片方だけ核が大きく「50%」となる頻度は0.5となります。
これを可視化します。
Pythonを使って実験を100000回試行して、「0%」「50%」「100%」と判断される頻度を見ていきたいと思います。
import random
import matplotlib.pyplot as plt
p = 0.5 #真の確率
n = 2 #一回の実験でカウントする細胞数
rn = []
for _ in range(100000):
tmp = 0
for __ in range(n):
jud = random.uniform(0,1) # 0-1の値を一様分布でランダムに返す
if p > jud: #p=1なら必ず真、p=0なら必ず偽
tmp += 1
rn.append(tmp/n) #表現型の割合として判断される値
plt.hist(rn,bins = 9,range=(0,1))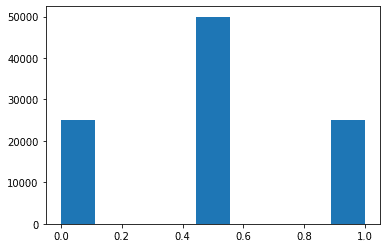
こうして、可視化できました。「0%(0.0)」と判断される相対頻度が25%、「0.5」と判断される頻度が50%、「1.0」と判断される頻度が25%になっているのがわかります。
ではこれをn= 30まで段階的に増やしていきたいと思います。
n = 5

n = 10

n = 30 ( binsを増やしました)

n = 100

こうしてみていくと、「表現型の割合」として判断される値の母集団の分布は正規分布っぽい、ということが見えると思います。
また、一回の実験でカウントする細胞数(n)を増やせば増やすほど、分布の幅が細くなることもわかります。
正規分布っぽいこの分布は二項分布と呼ばれています。実験の試行回数(今回は100000)を増やせば増やすほど、正規分布に近づいていきます。
「表現型の割合」の母集団は無限の試行回数で正規分布とみていいので、「表現型の割合」として判断される値はKS検定をするまでもなく、本質的に正規分布に従う存在なのです。(例外は後述)
・中心極限定理
「表現型の割合」が正規分布に従う理由である中心極限定理について。統計WEBによると、中心極限定理とは、
「標本を抽出する母集団が平均μ、分散σの正規分布に従う場合においても、従わない場合においても、抽出するサンプルサイズnが大きくなるにつれて標本平均の分布は「平均μ、分散σ2/n」の正規分布 に近づく」
なのだそうです。表現型が現われる確率というのは言い換えれば表現型がでる事象を1、出ないを0とした時の試行結果の値の平均値になるのでこの中心極限定理が使えるというわけです。
今回の場合、標本を抽出する母集団=表現型が出現するか否かの母集団は以下のベルヌーイ分布に従います。k=1のとき、P=p, k=0 のとき P =1-pとなります。
![]()
その分散はこのページの証明に従って、p(1-p)になります。
標本平均の分布は「平均μ、分散σ2/n」の正規分布 に近づく
ので、細胞カウント数が n のとき、表現型の出現率の分布の分散は、
V(X) = p(1-p)/n
となります。
直感的にベルヌーイ分布の分散がわかりにくいので、下では別の説明を試みます。
・二項分布の分散
事象の発生確率p、試行回数nとしたときの、事象が発生する回数の二項分布の分散V(X)は以下の式で表せます。
![]()
事象の発生確率p=0の時は事象の発生回数は必ず0回、p=1の時は必ずn 回であり、分散が0となることが考えれば納得できる気がします。最大の分散はp = 0.5の時に得られます。
分散が以下の式で定義され、xが2乗される値であることを考慮すると、(出典:アタリマエ!)

表現型の出現率の分布の分散は、np(1-p)をn^2で割って、p(1-p)/n となります。
当然先ほどと同じ結果です。
よって、n (実験あたりの細胞カウント数)を増やすことが、分散を小さくし、幅がシュットした分布を生みます。
・1%しか起きない事象の出現率
真の発生確率が50%の表現型を、30細胞でカウントした時に「判断される確率」の分布を以下に再掲します。

真の発生確率が変わると分布の平均が動きます。例えばp=0.3の時。

下図はp = 0.1。左側が0.0に近接して、正規分布かというと怪しくなってきました。

p = 0.01 (1%)。もはや正規分布とは言えません。ポアソン分布です。

このように、p が0や1に近づくと、最早正規分布とは言えなくなってしまいます。したがって、この時はT検定を使うべきではないという結論になるのです。
では、どうしたら客観的に正規分布か否かを判定できるでしょう?
・正規分布かどうかの判定
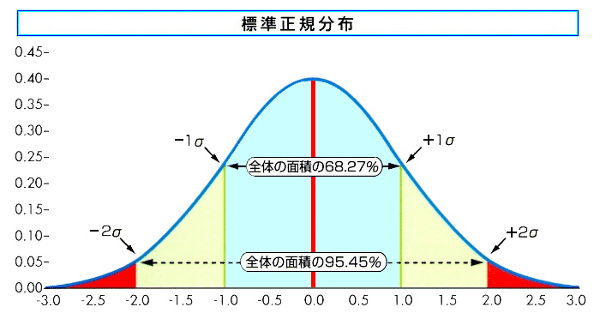
出典:サヤトレ
(調べても正確な方法がわからなかったのですが) ここでは標準偏差σを考えて、平均 ± 2 σ (全体の約95%)の裾野が0.0や1.0にかかっているときは正規分布ではないとみなします。
先ほどの議論から、σ = (p(1-p)/n)^(1/2)と表せます。
例えばn=30, p = 0.5 の時はσ = 0.09 となるので、95%範囲は 0.5 ± 2 * 0.09 を考えて、0.482 ~ 0.518 (赤線)となります。0や1にかかっておらず、正規分布であるとみなせます。

一方、n=30, p = 0.1の時はσ = 0.054で、95%範囲は−0.009 ~ 0.209 (赤線)となります。左側が0を下回っているので、正規分布とは言えないと考えられます。

ここで上部で記述した、サンプル数を増やすと幅が狭くなるという事実を考えると、n を増やせばp = 0.1でも正規分布と見なせるようになると考えられます。そこで、思い切ってn = 100にした場合、

こうなります。両方の裾野がよく収まっており、正規分布と見なしてよさそうです。T検定が使えます。
よって、低い確率でしか起こらない事象について検定したければ、多くの細胞を数える必要があるということがわかりました。
ちなみに冒頭の例のように5細胞しか数えない場合、n =5 の時の95%範囲はp=0.5でさえ0.05-0.94とギリギリであり、p = 0.6 だと正規分布とは言えません。5細胞でカウントするなら、T検定はほぼ間違いなく不可なのです。
・T検定
「表現型の確率の母集団は正規分布だ、T検定が使えるぞ」と分かったときの話です。
T検定は正規分布を前提とするので、何も前提としないU検定と比べて扱えるデータは選抜されており、その分だけ有意差も出やすくなっています(例外もあるようですが)。選べるならT検定を使いたいです。
T検定には、等分散を仮定するStudentのT検定と、等分散を仮定しない(別に等分散でも構わないがどちらでもいい)WelchのT検定という二つの方法があります。
「分散 等しい 検定」で出てくるのはF検定ですが、F検定をするのは不適です。表現型の出現率の場合、その値の分散は上で記載したように
確率の分布の分散は、np(1-p)をn^2で割って、p(1-p)/n となります。
と、pで決まる値であるためです。等分散を仮定した検定は初めから二群間に帰無仮説(同じp)が成り立つことを前提とする検定ということになり、不適切なのです。
したがって、表現型の出現率を検定するときは、WelchのT検定を使うのが良いと考えられます。
Pythonでは以下のように書くことができます。
#冒頭の例
import numpy as np
from scipy import stats
A = np.array([0.4,0.4,0.2])
B = np.array([0,0,0.2])
stats.ttest_ind(A, B, equal_var = False)
#equal_var = TrueでStudent, FalseでWelchの検定出力は
Ttest_indResult(statistic=2.82842712474619, pvalue=0.04742065558431962)となり、p = 0.047で有意差ありと言えます。
冒頭の例がもし大量の細胞を数えていて正規分布と見なせるのだとしたら、T検定で有意差ありという結論は正しかったのです。
・マン・ホイットニーのU検定
表現型の出現率の母集団が正規分布に従わない場合。使えるのは何の仮定も求めないマン・ホイットニーのU検定や、Fisherの正確確率検定です。この章ではU検定について記載します。
pythonでは、以下のようなコードで書くことができます。
#冒頭の例
import numpy as np
from scipy import stats
A = np.array([0.4,0.4,0.2])
B = np.array([0,0,0.2])
stats.mannwhitneyu(A, B, alternative='two-sided')出力は
MannwhitneyuResult(statistic=8.5, pvalue=0.11014892418594692)となり、p = 0.11で、有意差は認められないという結果になります。
・Fisherの正確確率検定
T検定にしてもU検定にしても割合で定量する場合には、何個の細胞を数えたかという情報が消えてしまいます。
すなわち、30個の細胞を数えて9個表現型が出た場合でも、一生懸命300個数えて90個の表現型が出た場合も同様に「30%」として評価してしまうということです。努力が報われません。
この問題を解消するため、直接に定量した細胞の”数”で分割表を作成し、Fisher正確確率検定やχ二乗検定を実施するということが可能です。
χ二乗検定は分割表のどこかに一桁の値があると適しないとされますが、Fisher正確確率検定は問題ないそうです。

分割表の例 (冒頭)
3回実験を繰り返して、各回の細胞の数を足し算して検定を実施します。
まずは上記の表の例(各条件5細胞、合計30細胞)で、Fisher正確確率検定を実施します。
#Fisherの正確確率検定
from scipy import stats
import numpy as np
con = [1,14]
treat = [5,10]
dat = np.array([con,treat])
odds, p = stats.fisher_exact(dat)
print(p)出力されるp値は0.17で、やはり有意差は認められません。
今の例の6倍、各実験で30細胞ずつ数えた場合は以下の分割表となり、

出力されるp値は9.92e-06となります。大きな有意差が見られました。
・T検定、U検定とFisherの正確確率検定の選択
で、結局何がいいのか?
今の例で各条件で数える細胞を変えて結果だけを示します。

Fisherの正確確率検定を使いましょう!
・結論
割合の定量はFisherの正確確率検定を使いましょう!
とはいえ、あまり受入れらていないという現実もあるので、U検定でもいいんじゃないかと思います。U検定でも有意差が出るような頑強な事象を見たいですね。
・最後に
以上になります。最後までご覧いただきありがとうございました。
自信をもって検定できるよう励みたいと思います。
この記事が気に入ったらサポートをしてみませんか?
