◆◆はじめに◆◆

第３章　コンピュータとプログラミング
学習１７　自然現象のモデル化

今回は、研修用教材に載っている範囲を流して説明しています。（PEP8に準拠させたくらい）

学習１１から解説してきた、「コンピュータとプログラミング」の章は、
この学習１７で終了です！

プログラミング系では、
Python超入門講座（９本）から数えて、１６本の動画になりました。

思っていたより行間を読むのが大変でした。

個人的な感覚ですが、
　・情報系の大学を卒業
 　・基本情報技術者試験 は合格している
　・Pythonの基礎は知っている
という人が教員研修用教材のみの内容で理解できるのは６～７割程度かなという感触です。

私自身も、かなり色々調べました（特にマイクロビット、探索・ソートアルゴリズム、円周率とモンテカルロ法）

いままで作成した動画は、その教員研修用教材からは理解が難しい、４割の部分についても、私なりに掘り下げて解説しているので、プログラム経験が浅い教員の方にも役に立つと思っています。

引続き、他の章の解説も行っていきます。

◆◆動画解説◆◆

◆◆文字おこし◆◆

今日は自然現象のモデル化とシミュレーションをPythonプログラミングで学んでいこう。

まずは、物体の放物運動のモデル化について説明するね。
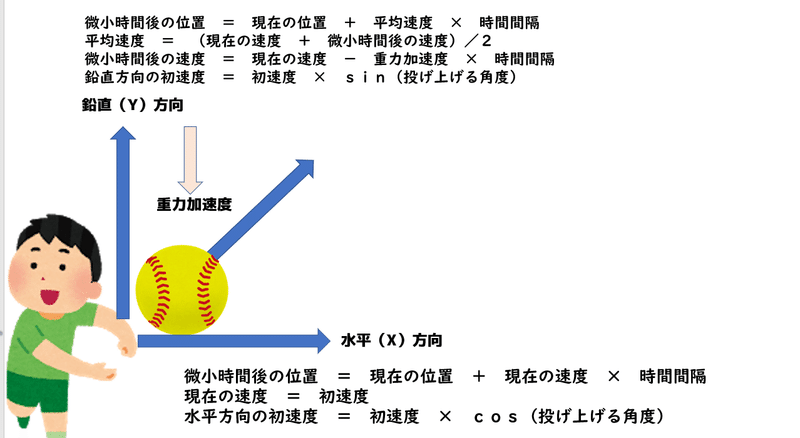
物体の放物運動をモデル化し，初速度と投げ上げる角度によって，物体がどのような軌跡を描いて飛んでいくのか，そして、遠くに飛ばすためにはどのような角度で投げるとよいのかということを考えていこう。
今回は、単純化するために空気抵抗を省いてモデル化するね。

物体の移動する軌跡は物体の水平（X）方向と鉛直（Y）方向の移動に分けて考え表現して，垂直方向は重力加速度を受ける。

まず水平方向について
水平方向は摩擦を受けないこととするね。
摩擦を受けないってことは、常に同じ速度で運動するから、任意の時点での加速度は初めの速度と同じ。
これを計算式で表すと
微小時間後の位置　＝　現在の位置　＋　現在の速度　×　時間間隔
現在の速度　＝　初速度
物体を投げ上げる角度と初速度から，水平方向の初速度は，
水平方向の初速度　＝　初速度　×　ｃｏｓ（投げ上げる角度）
となる。

次に鉛直方向について　
　鉛直方向は重力加速度によって速度が変化していく。任意の時点の速度に対し，微小時間後の速度は重力加速度の影響を受けて減少しているため，この間の速度の平均速度を使って算出するね。
　　　微小時間後の位置　＝　現在の位置　＋　平均速度　×　時間間隔
　　　平均速度　＝　（現在の速度　＋　微小時間後の速度）／２
　　　微小時間後の速度　＝　現在の速度　－　重力加速度　×　時間間隔
　　　鉛直方向の初速度　＝　初速度　×　ｓｉｎ（投げ上げる角度）
　　
となる。

この計算式をPythonプログラムに置き換えるんだけど

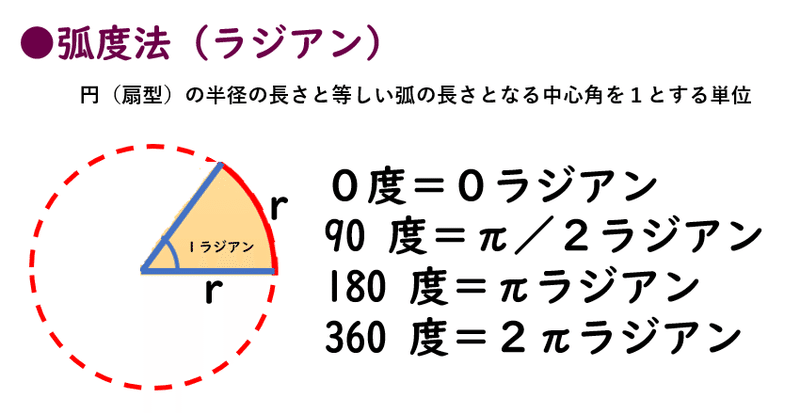
角度関連で弧度法（ラジアン）というものがある。
ラジアンは，
円（扇型）の半径の長さと等しい弧の長さとなる中心角を１とする単位で，
０度＝０ラジアン，90 度＝π／２ラジアン，
180 度はπラジアン，360 度＝２πラジアンとなる。
角度からラジアンへの変換は角度にπ／ 180 を掛ければよい。

今話した、放物線運動についてPythonでプログラミングするとこんな感じになる。

import math as math  # 数値計算ライブラリ
import matplotlib.pyplot as plt  # グラフ描画ライブラリ
dt = 0.01  # 微小時間(時間間隔)
v0 = 30  # 初速度
g = 9.8  # 重力加速度
x = [0]  # 水平位置の初期値0
y = [0]  # 鉛直位置の初期値は0
angle = 45.0 * math.pi / 180.0  # 投げ上げ角度
vx = [v0*math.cos(angle)]  # 水平方向の初速度
vy = [v0*math.sin(angle)]  # 鉛直方向の初速度
for i in range(1000):
   vx.append(vx[i])  # 微小時間後の水平方向の速度
   vy.append(vy[i]-g*dt)  # 微小時間後の鉛直方向の速度
   x.append(x[i]+vx[i]*dt)  # 微小時間後の水平位置
   y.append(y[i]+(vy[i]+vy[i+1])/2.0*dt)  # 微小時間後の鉛直位置
   if y[i] < 0:  # もし鉛直位置が0 を下回ったら
       break  # ループ中断
plt.plot(x, y)  # 位置の配列をプロット
plt.title("parabollic motion")  # グラフのタイトル
plt.xlabel("distance")  # x軸ラベル
plt.ylabel("height")  # y軸ラベル
plt.show()

数値計算ライブラリと、グラフを描くためのmatplotlibライブラリをインポートする。

dt 時間間隔　は0.01
v0 初速度 は３０
x 水平位置

vx 水平速度
y 鉛直位置vy 鉛直速度
g 重力加速度angle 投げ上げ角度

＝＝＝＝＝＝
変数　dt = 0.01 # 微小時間( 時間間隔)
v0 = 30 # 初速度
g = 9.8 # 重力加速度
x = [0] # 水平位置の初期値0
y = [0] # 鉛直位置の初期値は0
angle = 45.0 * math.pi / 180.0 # 投げ上げ角度
vx = [v0*math.cos(angle)] # 水平方向の初速度
vy = [v0*math.sin(angle)] # 鉛直方向の初速度

これをさっきの計算式に当てはめて、鉛直位置が０を下回るまでつまり地面に到達するまで、ループを繰り返す。

実行してみよう。

放物運動の軌跡が描かれたね。

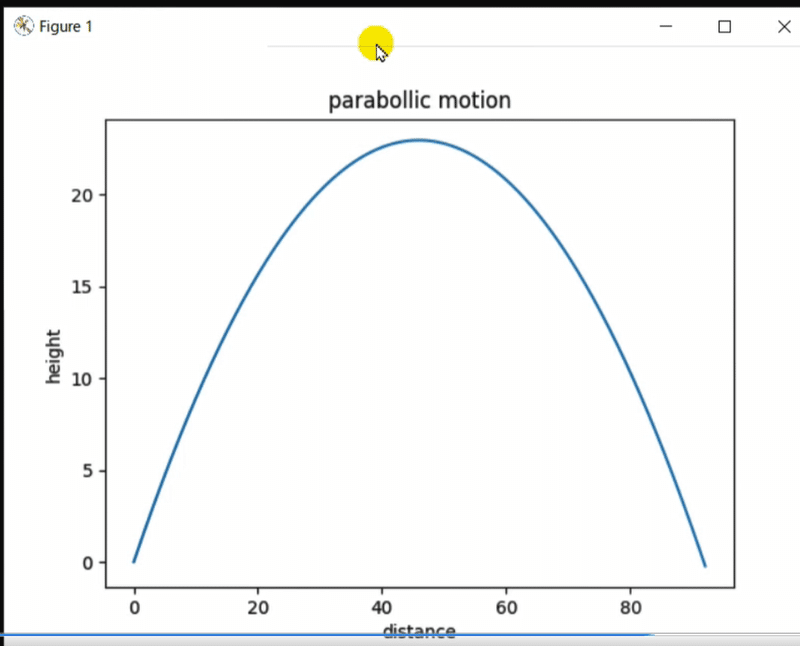
角度の変数を変えることによって、どの角度が一番遠くに飛ぶかを比較することも可能なんだ。

ーーー

今度は、生命体の増加シミュレーションをしていこう。
自然界における生物の個体数は，ある一定の環境内で一気に繁殖することがよく知られている。生存しうる個体数の上限を環境収容力と呼ぶね。
単位時間あたりに個体数が増加する数は，個体数×増加率で求めることができて，
個体数が多くなればなるほど増加数が増える。

　また，単位時間当たりに個体が減少する数は，個体数×減少率で示すことができて，増加数同様に個体数の数に比例して減少する。

一方，環境収容力と個体数の増加は個体の減少に強く働くこととなるため，
　減少率　＝　（現在の個体数／環境収容力）×増加率
と定義する。

この定義によって，個体数は環境収容力以上の数に増えると増加より減少数の方が増え，一方、環境収容力より個体数が少なければ増加数が増える。

今説明した内容をPythonプログラムでグラフを描いていこう。

import matplotlib.pyplot as plt  # グラフ描画ライブラリ
zouka = 0.01  # 増加率
capacity = 1000  # 環境収容数
n = [10]  # 最初の個体数
for i in range(1000):
   zoukasuu = n[i]*zouka  # 増加数
   gensyousuu = n[i]*(n[i]/capacity)*zouka  # 減少数
   n.append(n[i]+(zoukasuu - gensyousuu))  # 個体

plt.plot(n)  # グラフにプロット
plt.title("number of life")  # グラフのタイトル
plt.xlabel("time")  # x軸のラベル
plt.ylabel("number")  # y軸のラベル
plt.show()

zouka = 0.01 # 増加率
capacity = 1000 # 環境収容数
n = [10] # 最初の個体数

for i in range(1000):
そして、時間経過による増加数、減少数から個体数を求めて
最後にグラフを表示する。

実行してみよう。

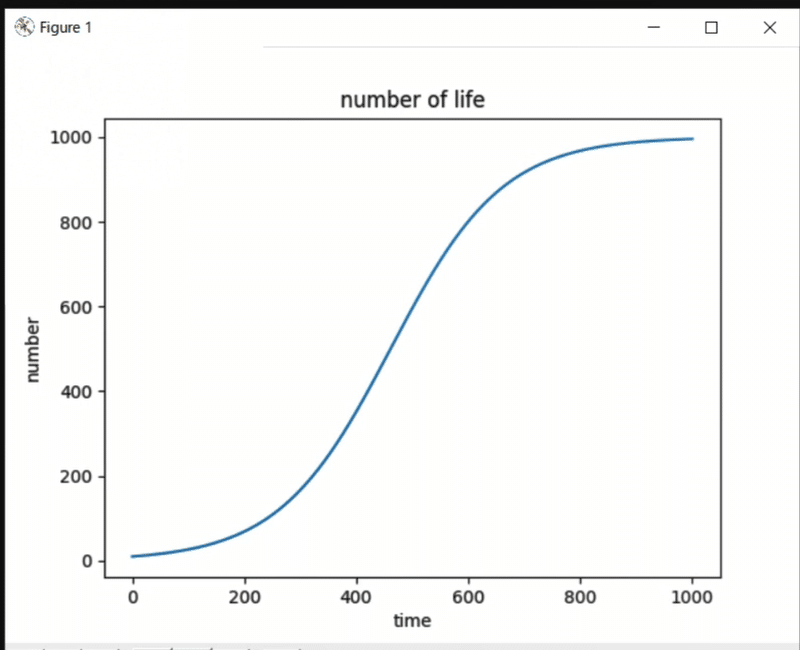
はじめは急激に増加して、時間と共に伸びが緩やかになっているね。

――――――――――
こんどはランダムウォークのシミュレーションをしていこう
ブラウン運動や株価の変動など，不確実な現象のシミュレーションとして用いられるモデルに，ランダムウォークがある。

　
　ある物体が次の時間変化後にどの方向に行くか予測できない状況で，その動く方向が一様な乱数に従う場合，
現在位置と次の時間変化後の位置との関係は，
　０～１の乱数を発生させる関数random() を用いると，
x = x0 + random( ) – 0.5
y = y0 + random( ) – 0.5
と表すことができる。この処理を1000 回繰り返してグラフに表示してみよう。

import matplotlib.pyplot as plt  # グラフ描画ライブラリ
import numpy.random as rd  # 乱数のためのライブラリ
x = [0]  # Xの初期値を0 にする
y = [0]  # Yの初期値を0 にする
for i in range(1000):
   x.append(x[i]+rd.random() - 0.5)  # X方向
   y.append(y[i]+rd.random() - 0.5)  # Y方向

trace = [x, y]  # XY平面状の物体の座標をtrace という名前の配列に代入
plt.plot(*trace)  # 配列要素のグラフ描画
plt.axis("equal")  # グラフの縦横比を等しく
plt.title("random walk")  # グラフのタイトルをつける
plt.show()  # グラフを表示

XとYの初期値は０とする
さっきの計算式に当てはめて、１０００回ループするようにして

結果をグラフに表示する。
実行してみよう。

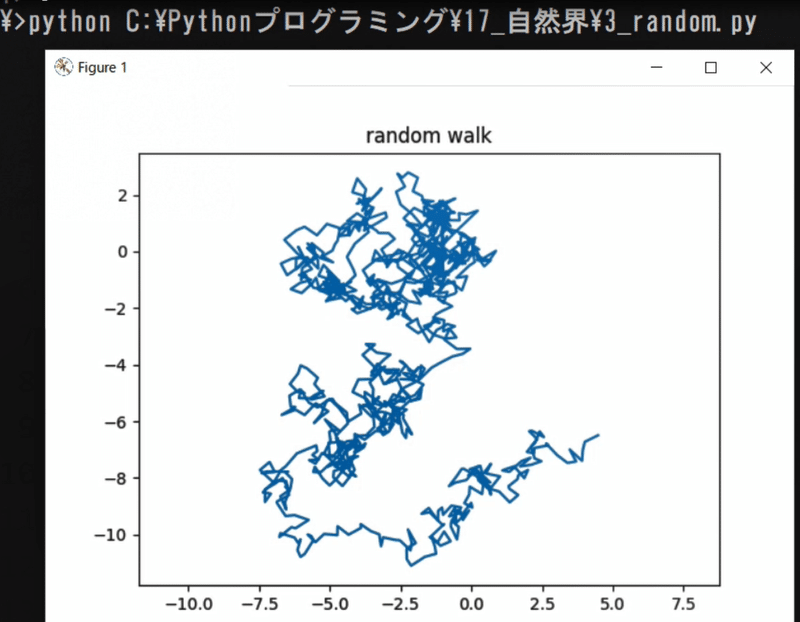
不規則な動きが描かれたね。

プログラミングを行うことで、自然界のいろんな事象をシミュレーションできるから、色んなパターンのシミュレーションをとおして知識を養うようにしよう。