【統計学】不偏分散について解説します

この記事では、統計の学習において、初学者がつまずきやすい不偏分散について解説していきます。
母分散・標本分散・不偏分散の関係を解説しながら、不偏分散は、なぜ、偏差平方和をデータ数n−1で割るのかについて、説明していきます。

分散とは

分散とは、データが平均値からどれだけ散らばっているかを表す統計量です。

具体的には、各データが平均値からどれだけ離れているか（＝偏差）を二乗し、それらを合計したもの（偏差平方和）をデータ数で割って計算します。

偏差をわざわざ二乗するのは、二乗しないと合計が0になるからです。
二乗ではなく絶対値にするという方法もありますが、数学的に二乗にした方が扱いやすいことから、二乗で計算しています。

分散が大きいほどデータは平均値から広く散らばっており、分散が小さいほどデータは平均値に集中しています。

例えば、5つの数値データとして、150、160、170、180、190があったとします。これの分散を計算してみましょう。

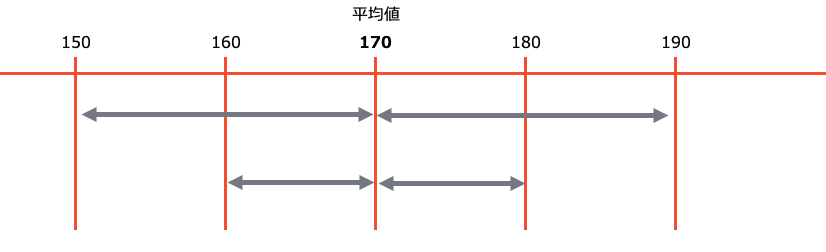
まず、平均値は、$${(150＋160＋170＋180＋190）÷5 =170}$$ですね。

分散は、$${[(150-170)^2 + (160-170)^2 + (170-170)^2 + (180-190)^2 + (190- 170)^2] /2 = 200 }$$です。

この分散の値をみただけでは、元のデータと比べたスケール感がよくわかりません。そこで、元のデータとの比較ができるよう、分散の平方根をとります。
これが標準偏差です。
この例だと、$${\sqrt{200}=14}$$です。各データの平均値からのバラつきが14ということです。

母集団と標本の関係について

分散がわかったところで、現実にあるデータを考えてみましょう。

統計の目的の一つは、限られた少ないデータで、そのバックボーンにある大きなデータを推測することです。

例えば、内閣支持率や視聴率がそうですね。全世帯を調査するのではなく、特定のデータを抽出して、そこから全世帯のデータを推測しています。

これらを表しているのが標本と母集団です

つまり、限られた少ないデータというのが標本、バックボーンにある大きなデータというのが母集団にあたります。

誤解を恐れずにいうと、母集団は神のみぞ知るデータです。

そんな神のみぞ知るデータを、母集団から取り出した標本を使って、推測するのが統計学なのです。

そして、母集団と標本の平均と分散のことを以下のように呼んでいます。

母分散と標本分散について

母分散と標本分散をもう少し詳しくみてみます。

母分散

母集団に属する全データについて、母平均との差の二乗和（偏差平方和）を求め、母集団のデータ数で割ったものになります。
記号では、$${σ^2}$$と表されます。
現実において、母分散は神のみぞ知る値です。

標本分散

母集団から抽出した標本データについて、標本平均との差の二乗和（偏差平方和）を求め、標本のデータ数で割ったものになります。
ここでのポイントは、標本分散は標本のデータ数nで割った値であることです。

不偏分散について

統計の目的は、標本を使って、母集団を推測することだと述べました。

この点、標本平均は母平均を推測するのに使えるのですが、標本分散はこのままでは母分散を推測するのに使えません。

なぜなら、標本分散は母分散より必ず小さくなっているからです。（その理由は後述します）

その小さくなっている分を補正し、標本分散の期待値が母分散に一致するように算出したのが不偏分散です。

不偏分散は、母集団から抽出した標本データについて、標本平均との偏差平方和を求め、それをn−1で割ったものになります。
標本分散から求めるとすると、$${標本分散×\frac{n}{n-1}}$$となります
記号では、$${S^2}$$と表されたりします。

なぜ、n-1で割るのか？

それは標本分散を求める式に鍵があります。
母分散を求める式、標本分散を求める式を比べてみましょう

分子をご覧ください。
母分散は母平均$${μ}$$との偏差であるのに対し、標本分散は標本平均$${\bar{X}}$$との偏差になっています。

これが何を意味するか？

標本平均は確率変数である

$${μ}$$は神のみぞ知る値ですが確定値です。変動しません。一方、$${\bar{X}}$$は標本データによって変動します。
つまり、確率変数なのです。

確率変数として、標本平均$${\bar{X}}$$にも分散があります。この分だけ標本分散に加えてあげないと母分散と一致しないのです。

それでは、標本平均はどの程度の分散になるのでしょうか？

これは中心極限定理によって、$${σ^2/n}$$と決まっています。

つまり、母分散$${σ^2}$$は、標本分散＋$${σ^2/n}$$で計算さえることになります。

$$
σ^2 = \sum(Xi - \bar{X})/n + σ^2/n 
$$

ですので、σについて解くと

$$
σ^2 = \sum(Xi - \bar{X})/(n-1) 
$$

つまり、$${\bar{X}}$$からの偏差をとった場合には、n-1で割らないと$${σ^2}$$と一致しないということです。

まとめ

標本データを使って母分散を推測したい時は不偏分散を使い、その場合は、標本平均との偏差平方和をデータ数ー1で割ると理解しておきましょう。

ただし、現実のビジネスの世界で、データを分析しようとする時は、データ数がそこそこ多いのが一般的です。
データ数が多ければ、偏差平方和をnで割ろうが、n-1 で割ろうが値はそれほど変わらないため、単純にnで割っても問題はないと思われます。