
同一画像検知アルゴリズムの紹介 Part1
こんにちは、プロダクト開発部のyuyaです。
私の記事は今回で3記事目になります。
1記事目と2記事目は、年齢確認書類の自動マスキングシステムについてご紹介しました。
まだ未読の方は、ぜひご覧ください。
今回は、同一画像検知アルゴリズムの紹介Part1になります。
背景
マッチングアプリのコンセプトにそぐわない利用を行おうをするユーザー(以下、不正ユーザー)は、複数のユーザーを作成し、同じ年齢確認画像を使い回す傾向があります。
マッチングアプリでは不正ユーザー対策の一環として、同一画像検知機能が稼働しています。
具体的には、ユーザーから年齢確認画像を受信した際に、過去にアップロードされた同じ画像を表示してくれる機能です。
今回は、そのアルゴリズムを2回に分けて詳しく紹介します。
解説の中では、視覚的にわかりやすいように図やアニメーションを用いています。

不正ユーザー画像の傾向
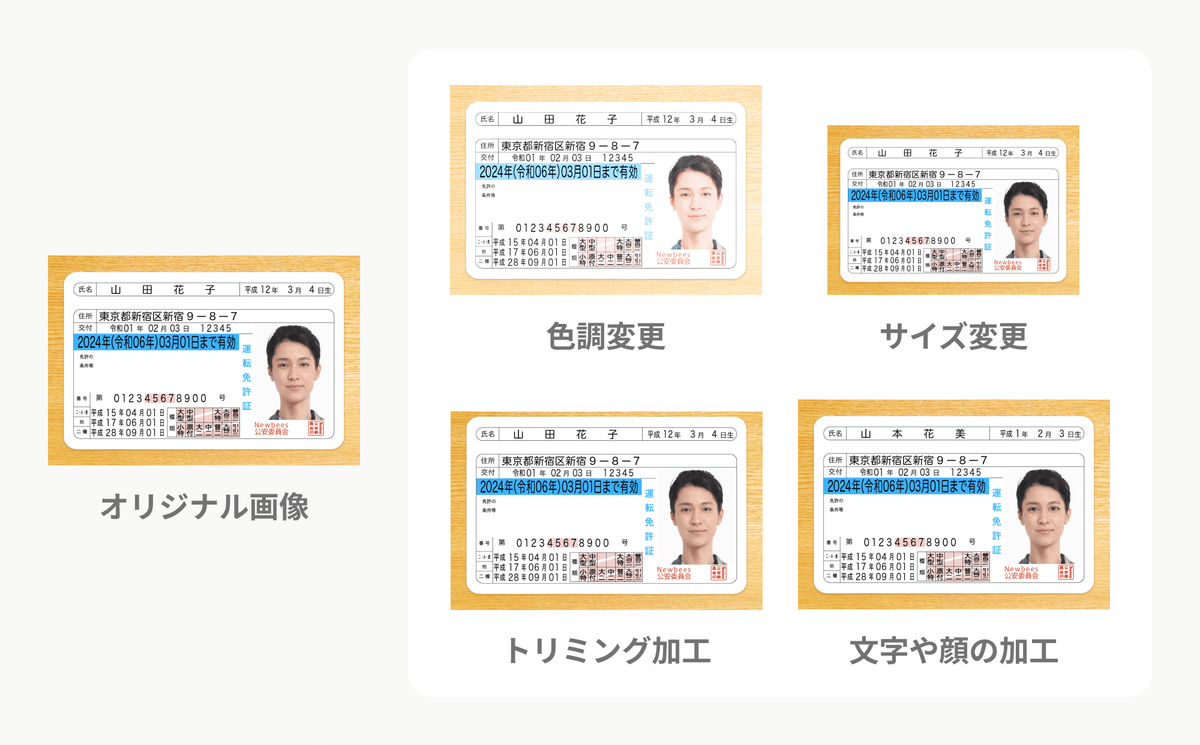
不正ユーザーが同じ画像を使い回す際には、全く同じ画像の場合もあれば以下のように加工されるケースもあります。
形式変更(ex. jpg->png)
画像サイズ変更
色調変更
トリミング加工
文字や顔写真の加工
方法
以上のような加工パターンもなるべく同一として判別するために、perceptual hash (phash)アルゴリズムを使いました。
phashは画像から人が知覚しやすい特徴を抽出し、64bitのハッシュ値に変換する処理です。

見た目が類似している画像同士の場合、phashで得られたハッシュ値間のハミング距離が近くなる特徴があります。
ハミング距離とは、ハッシュ値の各桁同士を見比べて異なる個数のことです。
この値で画像同士が類似するかどうかが分かり、0に近いほど似ていると判定できます。
見た目上異なる画像では、ハミング距離の値が大きくなります。
本システムでは距離4以下を同一と判定しています。


システムの全体像
年齢確認画像アップロード
ユーザーから年確画像がアップロードされたときのワークフローを、以下に示します。
受信した年確画像がAWSのS3にアップロードされると、それをトリガーにLambda内でphashが行われます。
その後、出力のhash値をDBに保存することで、phashで得られたhash値を保持します。

運営側の管理画面
同一判定をしている運営の管理画面のワークフローは以下の図になります。
Aさんの年確画像を受信し管理画面で表示するタイミングで、これまで不正ユーザー判定された画像とのハミング距離を求めて設定値4以下の画像を同一画像として表示しています。

システムの全体像の説明は以上になります。
次に、phashについて具体的に解説していきます。
phashの処理の流れ
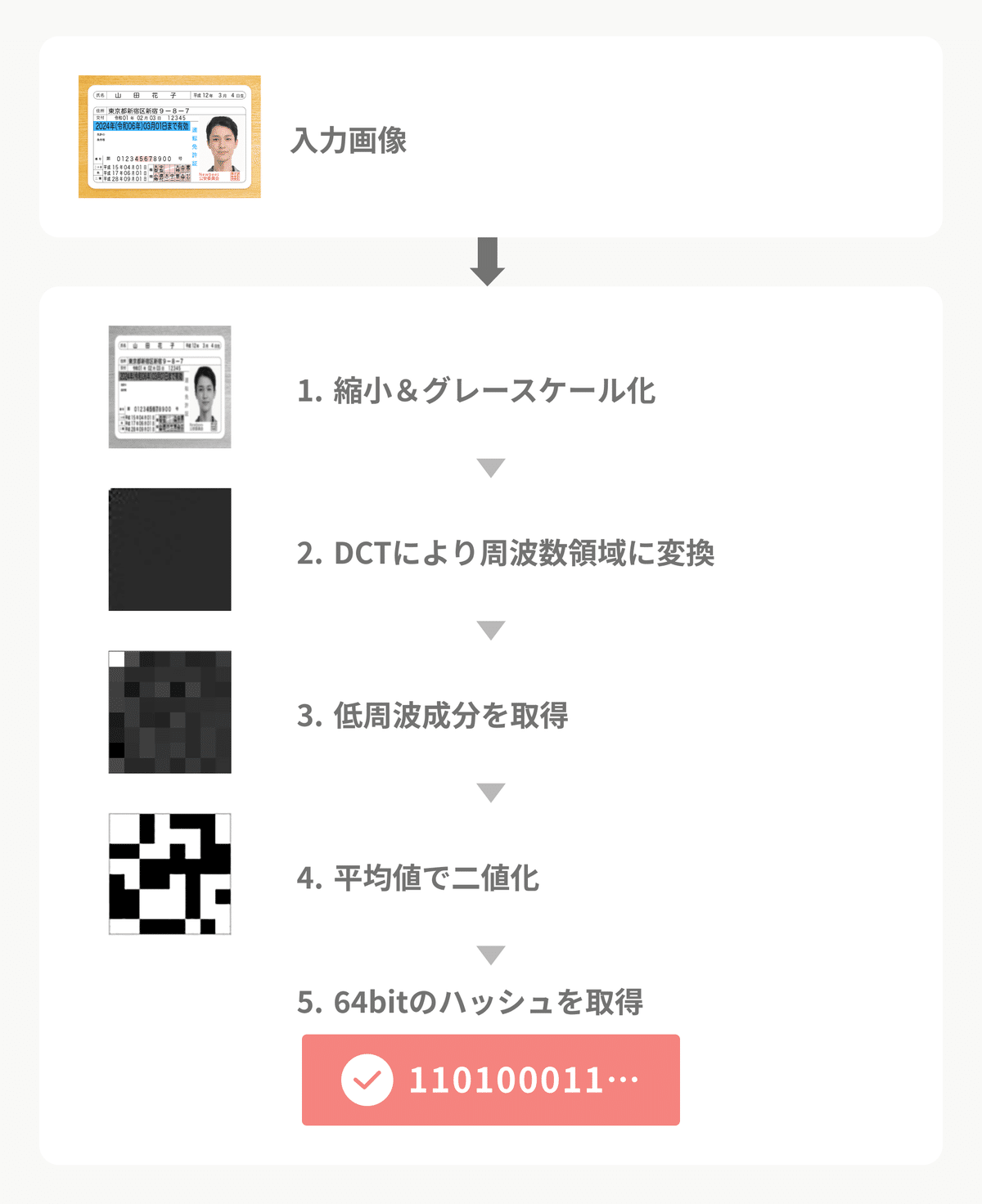
全体の処理の流れは、以下のようになっています。
縮小&グレースケール化
離散コサイン変換(DCT)により、周波数領域に変換
低周波成分を取得
平均値で二値化
64bitのhashを取得
各工程を順に説明していきます。
1. 縮小&グレースケール化
この工程は、次工程の計算を高速化し、最終的な出力を64bitにするために画像の情報を減らす工程です。
「縮小」では、どのようなサイズの画像でも出力を64bitに統一するために、画像サイズを64x64[pixel]に縮小します。
「グレースケール化」は、カラー画像(RBG)の3次元情報を1次元にすることで、後の処理を高速化します。

2.離散コサイン変換(DCT)
工程2では、縮小・グレースケール化した画像に対し、DCTという処理を行います。
DCTは、離散信号を振幅・周波数の異なる複数の正弦波へ変換する処理です。
phashのメインの工程なのでDCTについて詳細に解説します。

離散信号とは
離散信号は、自然に存在する音波などのアナログの情報をデジタル化して得られる信号のことです。
デジタル化では、音のような時間的に連続するアナログ信号を、コンピュータで扱うために一定時間ごとに波形を測定し、不連続な値に変換をします。
このような工程(サンプリング)で得られた離散的(不連続)な信号が離散信号です。
デジタル画像も同様に、現実世界の空間的に連続するアナログ信号を一定間隔ごとにサンプリングしているため、離散信号の1つといえます。
離散信号を正弦波で表現してみる
DCTとは「離散信号を振幅・周波数の異なる複数の正弦波へ変換すること」です。
例えば、以下の図の離散信号Xは、正弦波AとBの合成で表現できます。

グラフを重ねるとわかりやすいです。
波同士は重なる時に強め合ったり、打ち消し合ったりします。
x軸が0の時(グラフの一番左)、AとBが上方向に凸になり波同士が強め合うため、信号Xではさらに盛り上がっていることがわかります。
Xが100付近では、AとBが下方向に凸のため、同様に下方向に強め合います。
Xが75付近では、AとBが反対方向に凸になり打ち消し合うため、信号Xでは2つの波の中間の値を取ります。
このように、正弦波AとBを足し合わせると、信号Xのような波形になります。

信号Xは2つの正弦波の合成で表現できる単純な波形でした。
では、次のような角張った信号も正弦波の合成で表現できるのでしょうか?

答え:できる!
正弦波を1つずつ合成していくアニメーションを作ってみました。
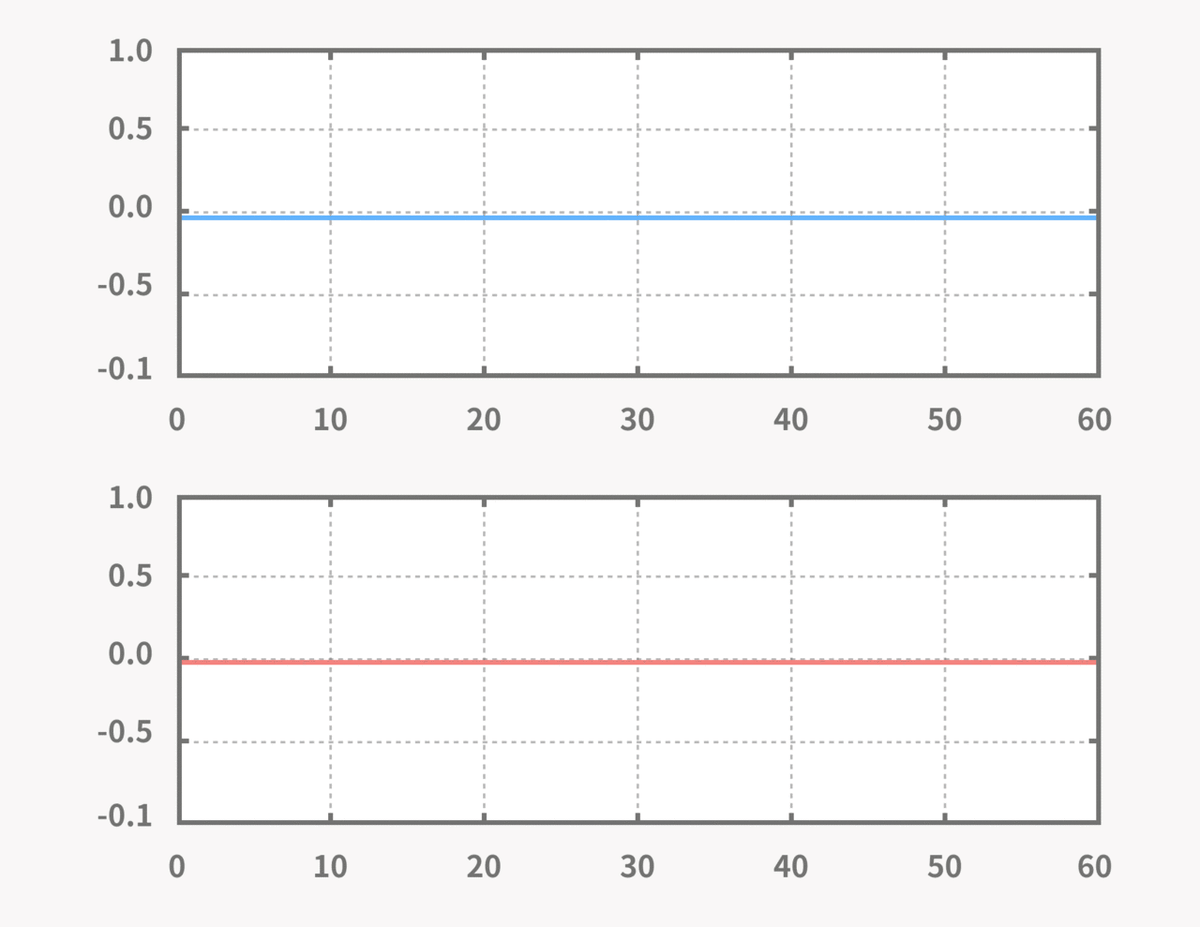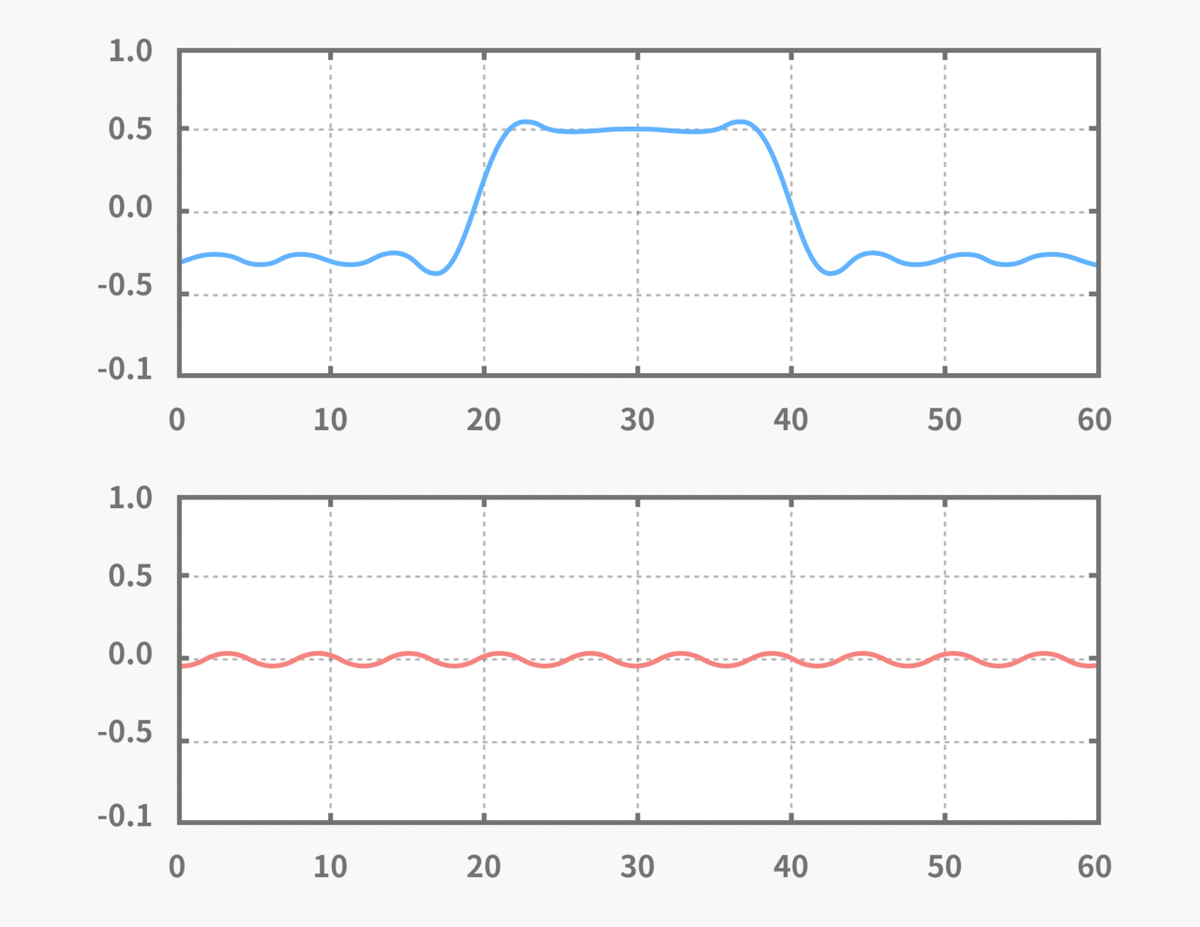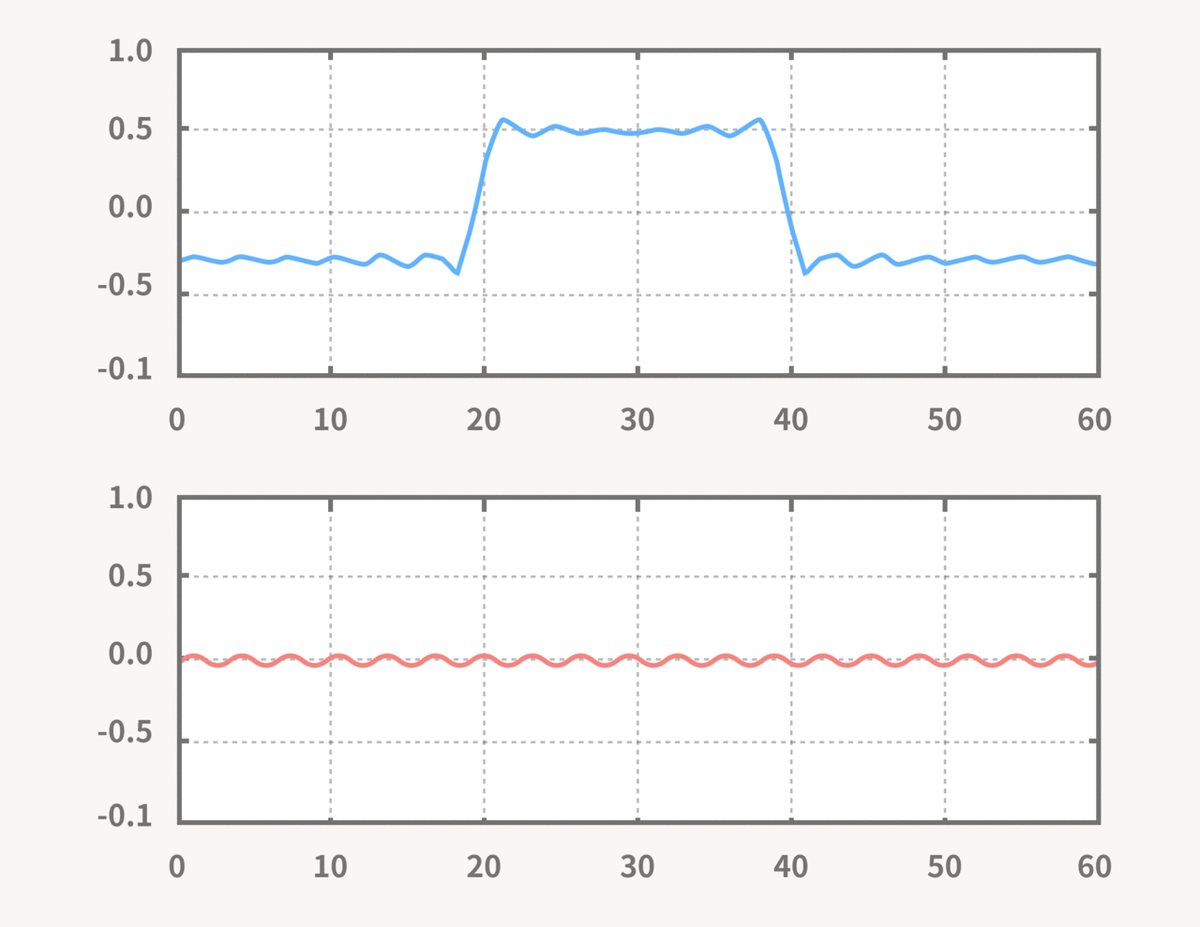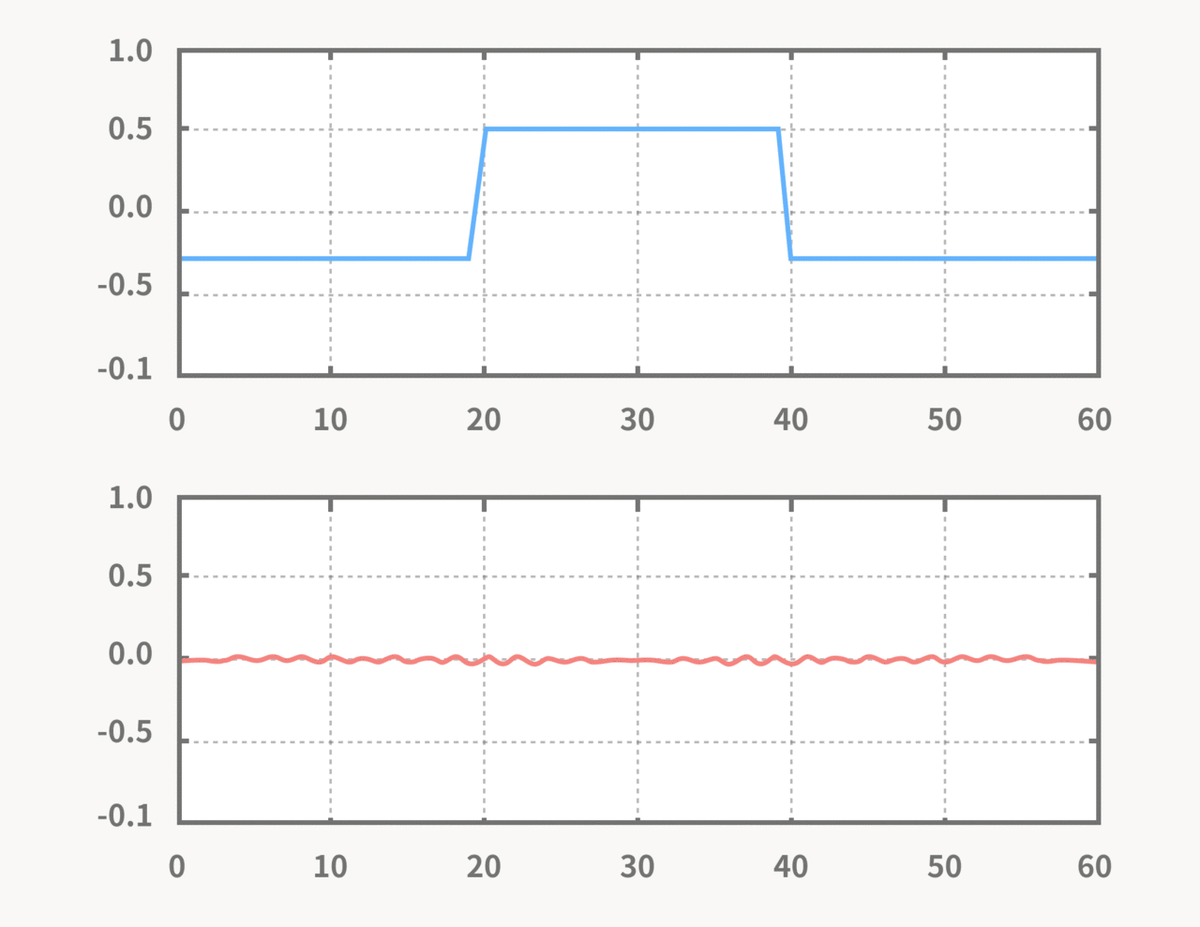
上のグラフが合成した結果の信号、下のグラフが合成する正弦波になります。
アニメーションでは、波の数が少ない正弦波(低周波)から順番に合成しています。
序盤の低周波の足し合わせをしている段階で大まかな山の形が作られ、その後に波が細かい正弦波(高周波)を合成していくことで、徐々に直線の波形になっていくことがわかります。
このように、どのような形の信号も複数の正弦波の足し合わせで表現できます。
DCTによって得られた離散信号を構成する正弦波の組み合わせのことを、周波数領域と呼びます。
画像のDCT
本題である画像のDCTについて説明します。
画像にDCTをかけると、以下のような周波数領域が得られます。(本解説は感覚的な理解の範囲に絞るため、周波数領域を得るための計算方法は省略します。)
周波数領域は一見ただの真っ黒の画像ですが、この中に入力画像を表現するための正弦波の組み合わせの情報が入っています。

以下に示す画像は、基底画像と言います。
画像を表現するために必要な正弦波の表みたいなものです。
全ての画像はこの表にある正弦波の重ね合わせで表現できます。
画像によって含まれている各正弦波の割合は異なります。
実際の基底画像は、右にも下にも正弦波画像が続いており、複雑な画像ほど使う正弦波の種類が多くなります。
右や下にいくほど高周波になっていきます。

基底画像の正弦波画像をグラフで表してみました。
縦軸が画素値、横軸が画素の位置です。
正弦波画像の黒い部分は正弦波の下に凹んでいる部分、白い部分は正弦波の上に凸になっている部分になっています。
このことより、基底画像各画像が正弦波を表していることがわかります。
正弦波のグラフを立体的に上から見た図のようなものです。

章の始めに示した、DCTにより得られる周波数領域を拡大してみました。
真っ黒ではなく、各画素に固有値が入っていることがわかります。

この各画素の1つ1つが基底画像に対応してます。
各画素値を数字で表現してみました。
画素の値は各正弦波がどれくらい含まれるかを表しています。
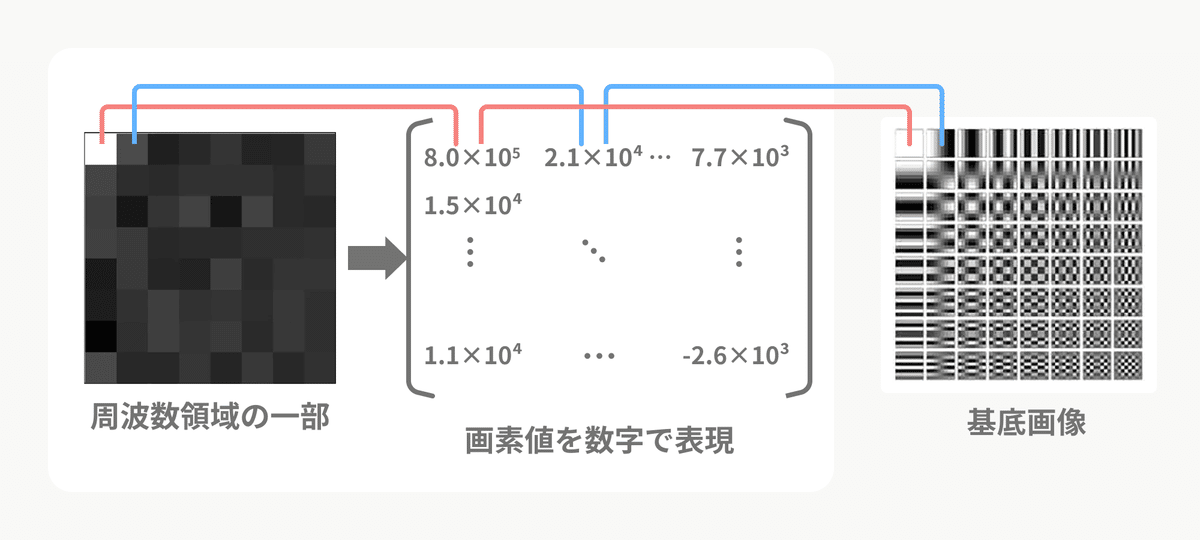
前章で信号を正弦波の足し合わせで再構成したように、DCTで得られた周波数領域から元の画像を再構成できます。
phashの工程に沿って、DCTの入力画像である64x64サイズのグレースケール画像を再構成してみます。
順番に正弦波を重ねていく様子をアニメーションにしてみました。
途中から早送りしていますが、正弦波画像を足していくことで入力画像と同じになりました!
このようにどのような画像でも振幅、周波数の異なる複数の正弦波の合成で表現できます。


まとめ
Part1では同一画像検知システムの概要と、phashの前半部分を紹介しました。
Part2ではphashの後半部分を説明します。
お楽しみに!
Newbeesでは一緒に働く仲間を募集しています
フルリモート勤務を導入し、場所にとらわれない自由な仕事のやり方が可能です。詳細は以下をご覧ください。
