
画像解析の内部紹介 〜OCR後の処理について〜
こんにちは、プロダクト開発部のyuyaです。
私の記事は今回で2作目になります。
前回は年齢確認書類の自動マスキングシステムについてご紹介させていただきました。
まだ未読の方はぜひご覧ください。
今回は前回紹介した画像解析システムのより内部についてのご紹介になります。
1.初めに
マスキング処理や生年月日抽出をするためには、OCRで検出された複数の単語から、対象の単語を決定する必要があります。
今回はベクトル演算を用いて、OCRのレスポンスである座標情報から、目的の単語を抽出する手順を紹介します。
画像解析や数学に興味がある方は、ぜひ読んでみてください。
2.背景
これまで、番号をマスキングする際は、「記号」「番号」などの表記を見つけ、その水平方向にある数字をマスキング対象としていました。
アプリエンジニアに、書類撮影時のカメラに枠線を引く機能を実装してもらったことで、斜めの角度で書類を撮るユーザーが減りました。
そのおかげで、マスキングの際は、水平方向の番号を探すフローでほとんどの対象を見つけることができました。
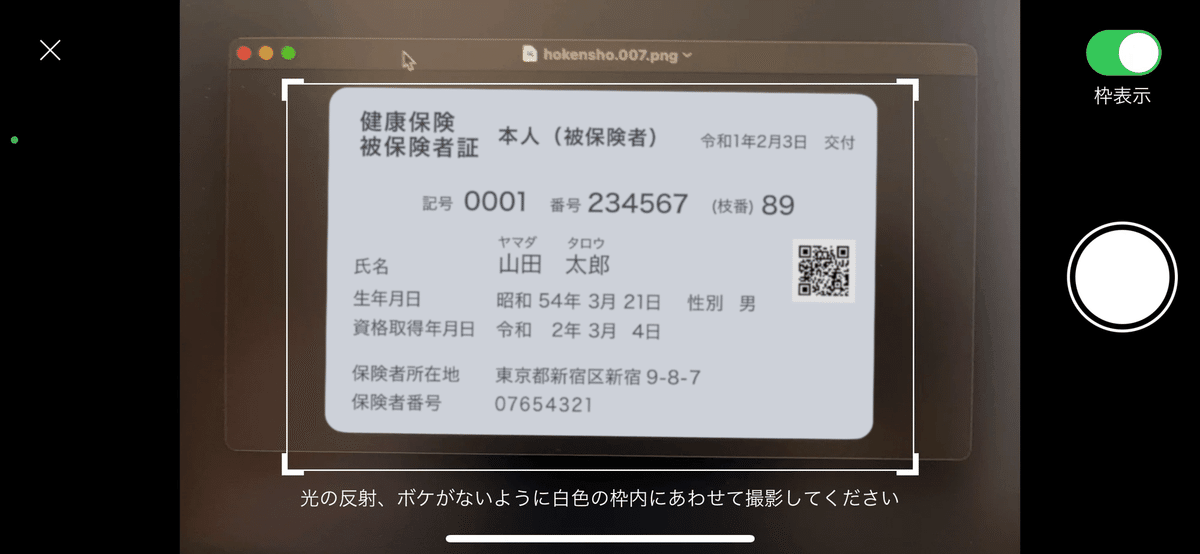
しかし、その後の追加案件で生年月日を抽出する必要が出てきました。
保険証には「生年月日」と日付の距離が離れているものが多く、写りが少しでも斜めになっている場合に水平の文字を探しても上手く抽出できませんでした。(マスキングの時は「記号」「番号」などの表記と数字の距離が近かったためあまり問題にならなかった)

そこで今回は水平方向ではなく「生年月日」の単語と同じ方向にある単語を探すように改良しました。

3.方法
OCRでは、検出された文字を囲む4点の座標が取得できます。
こちらは4点の座標を赤線で結んだ画像です。

この時に「生年月日」と同じ方向にある単語は「生年月日」を横切る線を横断しているため、「生年月日」を横切る線から見て単語の4点の座標が上側と下側の両方にあることがわかります。

対して、「生年月日」の方向にない単語は、「生年月日」を横切る線から見て4点の座標が上側と下側のどちらか一方に偏っています。


この特徴をアルゴリズムに落とし込むことで、今回の目的を達成できそうです。
そのために、sinθを使います。
こちらのグラフは、角度θに応じて決まるsinθの値を描いた曲線(サインカーブ)です。
0°<θ<180°の時にsinθは正、180°<θ<360°の時にsinθは負になることがわかります。

そこで「生年月日」の開始点と「生年月日」から見て上側にある単語の座標を結んだベクトルを作ります。「生年月日」ベクトルとのなす角θが0°<θ<180°になることが視覚的にわかります。
よって、「生年月日」の上にある単語のsinθは必ず正の値を取ります。

一方で「生年月日」の下側にある単語とのベクトルの角度は180°<θ<360°となるため、sinθは必ず負になります。

そして「生年月日」の線上にある単語の各ベクトルのsinθは正と負の両方を持つことがわかります。

4.sinθの求め方
実際に座標の値からsinθを求めてみます。
初めに「生年月日」を囲う4点の座標から左端と右端の縦の中心点を求めます。それぞれ点AとBとします。

A(ax, ay), B(bx,by)があったときベクトルABは(bx-ax, by-ay)で表します。
よってA(10, 80), B(110, 90)のベクトルABは(100, 10)になります。このベクトルの値はx方向に100進んだ時にy方向に10進むということを表しています。

「昭和」の左上の座標を点Cとし、同様の計算でベクトルACを求めます。

2つのベクトルが求められたので、ベクトルABとACのなす角のsinθを求めます。sinθを求めるためにはベクトルの外積の公式を使います。
ベクトルABとACの外積(AB×AC)の公式は2つあります。
①: AB×AC = |AB||AC|sinθ
②: AB×AC = (AB.x)*(AC.y) - (AB.y)*(AC.x)①と②の左辺が等しいため、右辺同士が等しい式を作ります。
|AB||AC|sinθ = (AB.x)*(AC.y) - (AB.y)*(AC.x)左辺の|AB||AC|を右辺に移動することでsinθを求める式に変形できました。
sinθ = {(AB.x)*(AC.y) - (AB.y)*(AC.x)} / (|AB||AC|)この式の分子 {(AB.x)(AC.y) - (AB.y)(AC.x)}にベクトルの値を代入してみます。
ベクトルAB(100, 10)、AC(200,40)より
sinθ = {(100*40) - (10*200)} / (|AB||AC|)
= 2000 / (|AB||AC|)
分母にある|AB|と|AC|はベクトルの大きさを表すため必ず符号は正になります。今回は符号さえわかれば良いので分母の計算は省略します。
分子と分母がともに正になるため、sinθが正になることが求められました。
「昭和」の左下の座標を点DとしベクトルABとADのsinθも求めてみます。

AB(100, 10)、AD(210,10)より
sinθ = {(100*10) - (10*210)} / (|AB||AC|)
= -2100 / (|AB||AC|)
分子が負になったため、sinθは負になることが求められました。
残りの2点の計算は省略しますが、「昭和」の4点のsinθで正と負の両方を含んでいることが分かったため、「昭和」は「生年月日」の同一方向上の単語と決定できます。
このように全ての単語において各4点のsinθを計算し、正と負の両方を含んでいるかどうかを見ることで、「生年月日」の同一方向上の単語の抽出が可能になります。
5.問題
これで無事終わりと思いきや、実は1つ問題があります。
sinθの符号を見るだけだと「生年月日」の同一線上にある後ろにある単語も各4点のsinθが正と負の両方を含むため、検出されてしまいます。

どうにかして「生年月日」の向き先にある単語のみをヒットさせたいです。

そこでcosθの出番です。こちらのグラフは角度θに応じて決まるcosθの値を描いた曲線です。0°<θ<90°と270°<θ<360°の時にcosθは正、90°<θ<270°の時にcosθは負になります。

「生年月日」の向き先にある「昭和」のcosθは4点全てが0°<θ<90°と270°<θ<360°を満たすため、4点全てが正になることが視覚的にわかります。

「生年月日」の逆方向にある「性別」のcosθは4点全て90°<θ<270°を満たすため、4点全てが負になることが視覚的にわかります。

4つのcosθの値が全て正になる単語のみを抽出することで、逆方向にある単語を省くことができます。
これでこの問題も解決できそうです。sinθと同様に実際にcosθを求めてみます。
6.cosθの求め方
cosθを求めるためにはベクトルの内積の公式を使います。
ベクトルABとACの内積(AB・AC)の公式は2つあります。
①: AB・AC = |AB||AC|cosθ
②: AB・AC = (AB.x)*(AC.x) + (AB.y)*(AC.y)
①と②の左辺が等しいため、右辺同士が等しい式を作ります。
|AB||AC|cosθ = (AB.x)*(AC.x) + (AB.y)*(AC.y)
左辺の|AB||AC|を右辺に移動することでcosθを求める式に変形できました。
cosθ = {(AB.x)*(AC.x) + (AB.y)*(AC.y)} / (|AB||AC|)
ベクトルABとACのcosθを求めてみましょう。
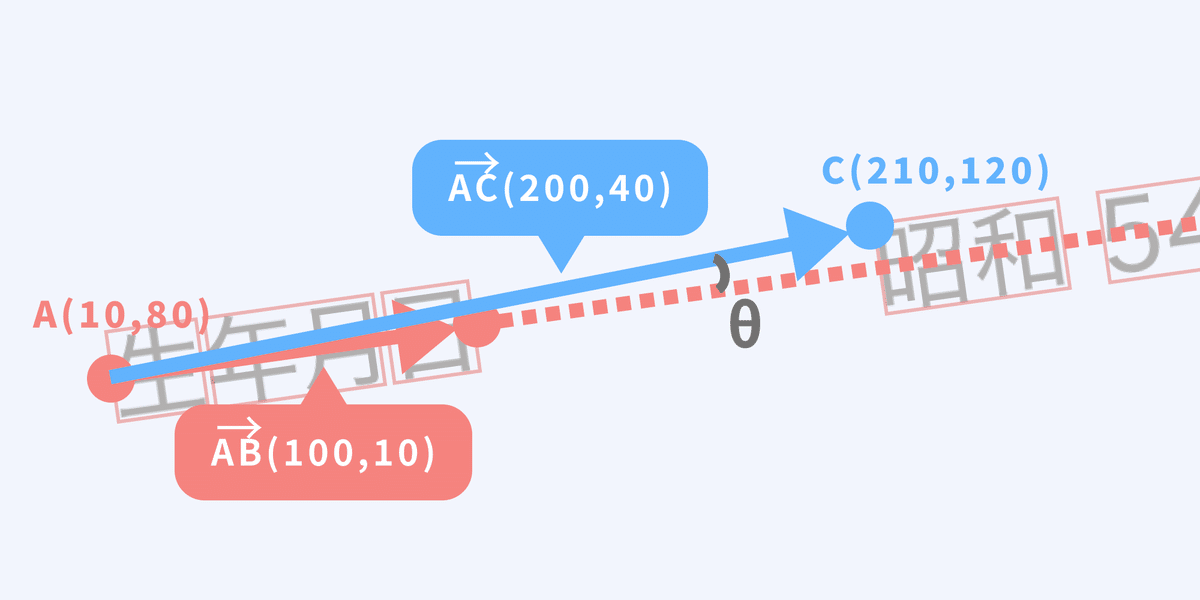
ベクトルAB(100, 10)、AC(200,40)より
cosθ = {(100*200) + (10*40)} / (|AB||AC|)
= 20400 / (|AB||AC|)
分母の(|AB||AC|)は必ず正になるため、cosθが正になることが求められました。
逆方向にある単語のcosθも求めてみます。

ベクトルAB(100, 10)、AE(-100,5)より
cosθ = {(100 * -100) + (10*5)} / (|AB||AE|)
= -9950 / (|AB||AE|)
分母の(|AB||AE|)は必ず正になるため、cosθが負になることが求められました。
このように内積を用いることでcosθの符号を求めることができます。
7.まとめ
全体の流れは以下のようになります。
1.sinθのフローにより「生年月日」と同一線上にある単語(「性別」「男」「昭和」「54」...)を抽出する。

2.cosθのフローにより逆方向にある単語を省く。
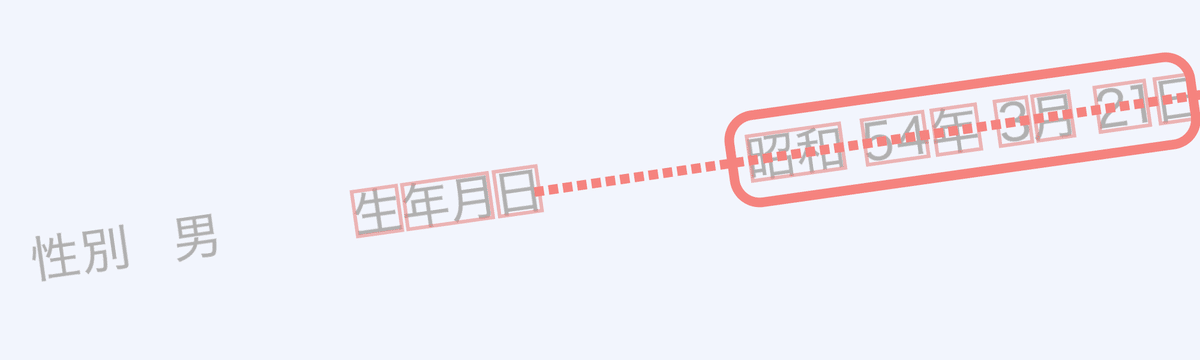
無事「生年月日」と同一方向の単語を抽出することに成功しました!
今回の記事を読んでいただくと分かる通り画像解析の中身は数学です。
単語のベクトル間のsinθ、cosθを求めることで、同一方向にある単語を抽出しました。
内積と外積を用いた計算は一見複雑のように見えますが、中身は座標の四則演算のため非常に少ない計算量で処理できます。
数学を用いることで問題解決ができる面白さを感じていただけたら幸いです。
Newbeesでは一緒に働く仲間を募集しています
フルリモート勤務を導入し、場所にとらわれない自由な仕事のやり方が可能です。詳細は以下をご覧ください。
