データ分析やAI開発に日頃携わらせて頂いているエンジニアの、バスケットボール上達アプローチ(※超素人編)
はじめに
皆さん、こんにちは。
データ分析やAI開発に日頃携わらせて頂いているエンジニアの私ですが、この度、バスケットボール上達のために行った調査等が、我ながらオタク感が強くて面白いかと思いましたので、紹介をさせて頂こうと思います。
尚、この記事は、私が所属するAnyTechという会社の、クリスマスアドベントカレンダーという企画に乗じて、書かせて頂いているものとなります。
その為、冒頭にAnyTechの紹介もさせて頂きます。
AnyTechは、日本の製造業を牽引するJFEグループに所属する、AIベンチャー企業です。
少人数ながら、最新技術を用いて、製造業を中心としたお客様の課題解決に取り組ませて頂いております。
採用活動も積極的に行っておりますので、もしご興味を持って頂けましたら、是非ともご連絡をよろしくお願い致します。
なぜ、バスケットボールなのか……w
さて、冒頭から唐突な出だしにて、大変恐縮です。
私、先日、馬齢40となりましたオッサンですが、昨今のご時世や子供の影響などから、バスケットボール(プレイする方)にすっかりハマってしまった次第です。
周囲からは、「悪い意味で不惑」と、冷ややかな目で見られております。笑
しかし、個人としましては、10kgのダイエットに繋がったり、日常の楽しみが増えたりと、良いことづくめです。
また、幾つになっても、できなかったことができるようになる達成感は、心地が良いものです。
尚、小職のバスケットボールの経験ですが、学生時の体育授業や、昼休みのレクリエーション等でカジッていた程度でして。
むしろ、最も苦手意識を持っていたスポーツがバスケットボールであった、と言っても過言ではありませんでした。
その為、「子供にバスケを教えてって言われたら、どうしよう…。」という懸念を、心のどこかに抱えておりました。
そんな折、YouTubeに上げられていた、ステフィン・カリー選手のスゴ技プレイを拝見しました。
ステフィン・カリー選手は、ポイントガードでありながら、3Pシュートの成功数が歴代1位であるというスター選手です。
スラムダンクで言えば、三井寿と宮城リョータとをフュージョンさせたような、ゴジータ的なプレイヤーです。
そんなカリーきっかけで色々調べてみると、現在のNBAはルール改正の影響もあり、いわゆるマイケル・ジョーダン全盛期の頃と比べ、1試合平均の3Pシュート数が、投球数/成功数共に2倍以上に増えているのだそうです。
以下の3Pシュートに関するwikiが、その推移についてまとめてくれていました。
また、更に調べていくと、第一線で活躍する選手の多くは、ミドルレンジ以上のシュートを多用しているようでした。
クリス・ポール選手、ケヴィン・デュラント選手、トレイ・ヤング選手、ルカ・ドンチッチ選手、等々…。
レブロン・ジェームズ選手などは、若き日はフィジカルを活かしたプレーでならした選手だったそうですが、昨今では3Pシュートも多用する選手へと進化し、御年37歳にて、今尚スーパースター選手として活躍をしているようでした。
即ち、ミドルレンジ以上のシュートの重要性が上がりつつあるNBA模様な訳です。
(細かい話をすると、深めの2Pシュートを打つくらいなら、少し下がって3Pシュートを打った方が、得点効率が高いという風潮であるようです。)
そして、そんな調査結果から、「逆に言えば、シュートがポンポン入るようになれば、素人でも試合に参加できたりするのか…!?」という、前向きな意欲が芽生えてきました。笑
幸い、友人のバスケットボール経験者が、定期的に集まってはプレイをしているとのことで、そこで迷惑をかけないことを目標に、練習を始めた次第でした。
尚、ズブの素人である為、シュート練習に向けては、バスケットボールを先ず購入する必要があったのと、買うべきボールの規格等についても学ぶ必要がありました。
しかし、そこは現代情報社会の有り難さ…。
検索すれば、すぐに答えに辿り着ける為、キャッチアップにそう時間はかかりませんでした。
バスケットボールのシュートは、ゴールへの入射角が45°になるように打つべし
さて、シュート練習をするに当たって、先ずは、シュートはどのように打つものなのかを調べてみました。
昔カジッていた頃には、全然シュートが入らなかった覚えがあり、闇雲に練習しても上達が難しいかもしれない、という危惧が大いにありました。
色々調べてみましたところ、スポーツのレクチャーですと、やはりYouTubeがズバ抜けて分かりやすかったです。
既に活用されている方はご存知かと思いますが、プロの選手や著名なコーチなどが、チャンネルを開設してノウハウを公開してくれていたりします。
良い意味で情報バブル状態といいますか、情報化社会の恩恵が極まっている印象です。
もの凄く有り難い時代ですね。
そして、現代NBAに憧れてバスケを始めた私にとって、特に刺さったYouTube動画は、eHoopsさんがまとめて下さっている「シュートフォーム確立・改善」という動画集でした。
この動画では、NBAスキルコーチのドリュー・ハンレンさんが、シュートの打ち方を、非常に分かりやすく解説して下さっています。
或いは、eHoopsさんの和訳や切抜のセンスが光っているとも思います。
時に抽象的に、時に具体的に、特に目的論的に、特に例示を挙げながら。
この辺りは仕事上でのプレゼンテクニックや、レクチャーテクニックとしても、非常に参考になると思った次第です。
尚、本筋であるシュートの打ち方についてですが、人は身体構造が各々異なる為、一概にこうだとは言えないそうです。
一方、そんな中でも、「一流の選手が、共通して実践しているシュートの打ち方」という、先程の逆説的なものが存在するのだそうです。
つまりは、その共通ノウハウを参考にしながら、一方で、個々人における調整/アレンジを加えていくことが、上達への近道であるとのことでした。
いやはや…、これは言われてみると当たり前に思えますが、なかなかどうして…、型にはめ過ぎてしまったり、こだわり過ぎてしまったり、或いは、逆に自己流で遠回りをしてしまったり。
それは悲しいかな、スポーツの練習をする上での、あるある思考停止かと思います。
或いは、仕事や生き方にも通づるような、合理的、かつ、クレバーな講釈であると思いました。
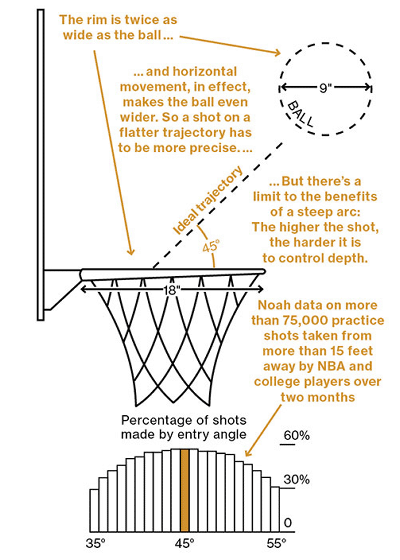
さて、その「一流の選手が、共通して実践しているシュートの打ち方」についてですが、幾つか紹介されている中で、私が最も感動したのが以下図でした。
この図が伝えたいメインメッセージは、「シュートは、ボールがゴールに対して、45°の入射角で飛び込む場合に、最も成功しやすい」という仮説になります。
或いは、これは、NBA・WNBA・大学・高校などのプロ・アマチュア問わず、様々なレベルのプレイヤーのシュートの結果を、研究者の方が集計した統計情報なのだそうです。
図中に、75,000以上のシュート練習から得た情報だと書かれています。
また、15feet(4.57m)以上離れたところからのシュートとも書かれています。
(確かに、ゴール下等から打たれたシュートについては、45°という法則は、直感的にも当てはまらなそうな気がします…。)
詳細につきましては、是非とも以下記事を参照頂けたらと思います。
ここで、「45°の入射角となるようにシュートを打つ」とは、とても具体的で、直感的に分かりやすい仮説です。
身体を用いてパフォーマンスするバスケットボールにおいて、具体的、かつ、直感的なノウハウというのは、非常に有益なものでしょう。
また、入射角に当たりをつけ、それを統計的に求めようと考えたセンスは、なんとも素晴らしいと興奮してしまいました。
日頃、データ分析の仕事をやっていると、よもや分析の技術よりも、こういった仮説立てのセンスが、最も功を奏すようなケースが少なくはないと思います。
この仮説を元に、実際にシュート練習向け製品の導入にも至っているとのことで、諸々見習うべき部分が多いと感じた次第でした。
尚、ここでつぶさにグラフを眺めてみます。
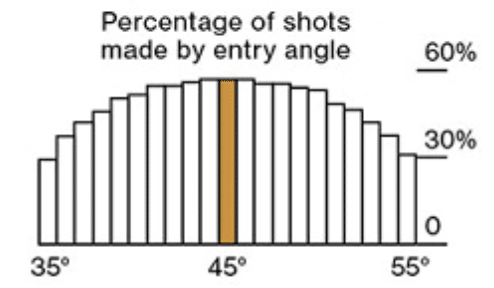
「あれ、別に40°や50°でも、45°とそう変わらないんじゃないか…?」と思った方がいらっしゃったとしたら、鋭い感覚をお持ちだと思います。
実際、ステフィン・カリー選手は46°なんだそうです。
これは、先程の話と同様、あくまで基準とすべき角度が45°であり、各人によっての調整余地はある、ということかと思います。
尚、「ボールコントロールの正確性」と「アーチの高さ」との間には、トレードオフの関係性があるかと思います。
例えば、野球のピッチングでも、勢いよく投げる方が、山なりで投げるよりも、コントロールがつけやすいかと思います。
バスケットボールでも同様に、例えば、ボールをリングに当てるという目標となれば、勢いよく投げた方が比較的当てやすいかと思います。
一方で、ボールをリングに通すことを考えると、バスケットのゴールが上を向いている性質上、アーチが高ければ高い程、即ち、入射角が90°に近ければ近い程、ボールがリングを通りやすくなり、リングに弾かれる可能性が低くなります。
入射角が大きい方がリングに弾かれる可能性が低いことは、以下ページにて分かりやすく解説がされていますので、是非とも参照下さい。
そのように、「ボールコントロールの正確性」と「アーチの高さ」との間に、トレードオフの関係性がある中で、45°という角度が、調査上にて成功確率が最も高い為に、1つの推奨される角度である、というのが先の主張かと思われます。
入射角45°を、どう確認するか…?
しかし、ここで素朴な疑問が浮かびます。
45°の入射角で打てているかどうかは、どのように確認すれば良いのでしょうか?
具体的な指針ながらも、果たして確認の術があるのかという疑問にかられてしまいます。
NBAなどでは、シュートの入射角を計測するNoahという機器が導入されているとのことです。
Noahは、ボールがリングを通過したタイミングにて、音声で入射角が幾つだったかを教えてくれるのだそうです。
ちなみに、Noahですが、内部的にはkinectが用いられているのだそうです。

しかし、そんな機器のない素人の私は、一体どうすれば良いでしょうか?
NBAなどでは、リターンが期待できるために、機器への投資ができますが、1個人ではなかなか…。
カメラ撮影で上手く計測できないかを考えましたが、シュートを打つ度にそれが確認できないと、練習としては効率が悪いかと思いました。
また、カメラ位置をゴールの高さである3.05m、かつ、真横アングルにセットできないと、入射角の計算には少々骨が折れそうです。
更には、カメラのレンズも歪みがあったりしますので、それも考慮するとなると…。
流石に、その計測にかける時間を、練習に回した方が良さそうな気がしてきてしまいます。笑
色々と思慮した結果、私は、ミニチュアを用いてシュート視野を再現することを思い付きました。
自分から見て、大体どのくらいの高さにボールが上がっていれば、十分なアーチを描けているかという参考になるのでは、と思った次第です。

ミニチュアの用意
さて、思い立ったが吉日、早速取り掛かっていきます。
先ずは、以下のレブロン・ジェームス君人形を買ってみました。笑
映画とのコラボでしょうか。
非常に、ポップな仕上がりです。

こちら、購入後に計測してみると、身長が30cmでした。
レブロン・ジェームズ選手の実際の身長は206cmとのことなので、1/6程のスケールになります。
ボールの大きさは、円周が11cm程だったので、そこから計算して、直径が3.7cm程でした。
6倍すると、22.5cm程となる為、NBAの公式球の直径24.5cmと比べますと、少し小さめに作られているようです。
尚、私の身長170cmをベースとして、今回は視野を再現したいので、ボールの大きさは相対的に更に小さくなってしまう形になります。
しかし、本検証にて知りたいのはボールの高さですので、そこは我慢しようと思います。
さて、この人形を身長を170cmと見立てて、ミニチュアを作っていきます。
30cmの人形を170cmと見立てる場合、305cmのゴールは53cmとなります。
45cmのゴールのリング(リム)は、8cmとなります。
フリースローラインまでの距離4.225mは、75cmとなります。
そんな風に計算しつつ、作成したミニチュアが以下写真となります。

シュート軌道の計算
次に、シュートの軌道を計算します。
今回は、4.225m位の距離、即ち、フリースローライン辺りからシュートを打つケースを考えたいと思います。
尚、放物線の式は、2次方程式となることが知られている為、求める軌道の方程式は y = ax² + bx + c となります。
また、今回は空気抵抗は無いものと考えます。
シュートを放つ位置の高さは、自分の身長に10cmを加えた1.8mとします。
この点を座標A:(0, 1.8)とします。
ゴールの高さは、3.05mで、シュートを打つ位置を4.225mとします。
この点を座標B:(4.225, 3.05)とします。
また、入射角が45°ということで、以下のような三角形を考え、その横の長さを30cm、縦の長さを30cmと置いて、そこを通過すると考えます。
この点を座標C:(3.925, 3.35)とします。

この図でいうと、三角形の上にある「BALL」と書かれた位置が座標Bであり、三角形の下にあるゴールの位置が座標Cとなります。
即ち、3つの座標A/B/Cの位置関係は、少し分かりづらいですが、以下の図示となります。
(※後程、イメージの重ね合わせも実施します…。)

尚、図示はpythonで行っています。
キャッチーな話から、急に専門的になってしまい恐縮ですが、エンジニアの方向けにコードも共有させて頂こうと思います。
import numpy as np
import matplotlib.pyplot as plt
x = np.array([[0],
[4.225],
[3.925]])
y = np.array([[1.8],
[3.05],
[3.35]])
plt.figure(figsize=(10, 10), dpi=100)
plt.scatter(x, y, s=200, alpha=0.5)
plt.xlim([-0.5, 5.5])
plt.ylim([-0.5, 5.5])
plt.grid()
plt.show()また、求めるべき放物線の式は、y = ax² + bx + c という形の2次方程式となります。
この2次方程式は、通過する点が3つ与えられますと、その係数a・b・cの最も尤もらしい値を求めることができます。
いやゆる、最小二乗法という統計手法を用いてです。
(※こちらも、急に話が統計寄りの内容になってしまい恐縮ですが、分かる方向けに…。🙇💦)
そうして求めた放物線が以下となります。
求められた係数は、a = -0.33、b = 1.691、c = 1.8 となりました。
つまり、放物線の式は、y = -0.33x² + 1.691x + 1.8 という2次方程式となります。
放物線を描画してみると、以下となります。

この直線式を求めるコードと、それを描画するコードは、以下となります。
x = np.concatenate([x**2, x, x**0], axis=1)
w = np.linalg.inv(x) @ y
x_ = np.arange(-2, 7, 0.01)[:, np.newaxis]
x_ = np.concatenate([x_**2, x_, x_**0], axis=1)
y_hat = x_ @ w
cmap = plt.get_cmap("tab10")
plt.figure(figsize=(10, 10), dpi=100)
plt.scatter(x, y, s=200, alpha=0.5)
plt.plot(x_[:, 1], y_hat, linewidth=7, alpha=0.5, color=cmap(1))
plt.xlim([-0.5, 5.5])
plt.ylim([-0.5, 5.5])
plt.grid()
plt.show()座標点の数と係数の数が合致している為、逆行列を用いますと、シンプルに解くことができます。
プログラム上は、係数a/b/cは、w = {a, b, c} となる形で、1つの変数にまとめられています。
この描いた放物線上に、ネット上で見つけたイラストを拝借させて頂き重ねると、以下のようになります。

どうやら、良い感じに放物線が描けていそうです。
シュート軌道上のボールの見え
さて、最後にですが、レブロン・ジェームズ君人形と、ボールと、ゴールのミニチュアを用いて、ボールの高さを相対的に撮影していこうと思います。
尚、求めた放物線の方程式は、y = -0.33x² + 1.69x + 1.80 というものでした。
水平飛距離の1m・2m・3mの地点、及び、ボールが放物線の頂点に達する2.56mについて、放物線の高さの値を求め、それをミニチュアで再現しながら撮影していきます。
ボールの水平飛距離1mの地点です。
ボールの高さは、3.16mとなります。
ミニチュア上は、水平飛距離17.6cm、高さ55.7cmとなります。

図の緑色の位置にいるボールが、シュートしたプレイヤーからは、以下のように見えます。

続いて、ボールの水平飛距離2mの地点です。
ボールの高さは、3.86mとなります。
ミニチュア上は、水平飛距離35.3cm、高さ68.1cmとなります。


続いて、2.56m。
ボールの高さは、3.96mとなります。
ミニチュア上は、水平飛距離45.2cm、高さ69.9cmとなります。
尚、これが、ボールが最高点に達しているタイミングになります。
以降は、重力に負けて、ボールが下がっていきます。


続いて、3mです。
ボールの高さは、3.90mとなります。
ミニチュア上は、水平飛距離52.9cm、高さ68.8cmとなります。
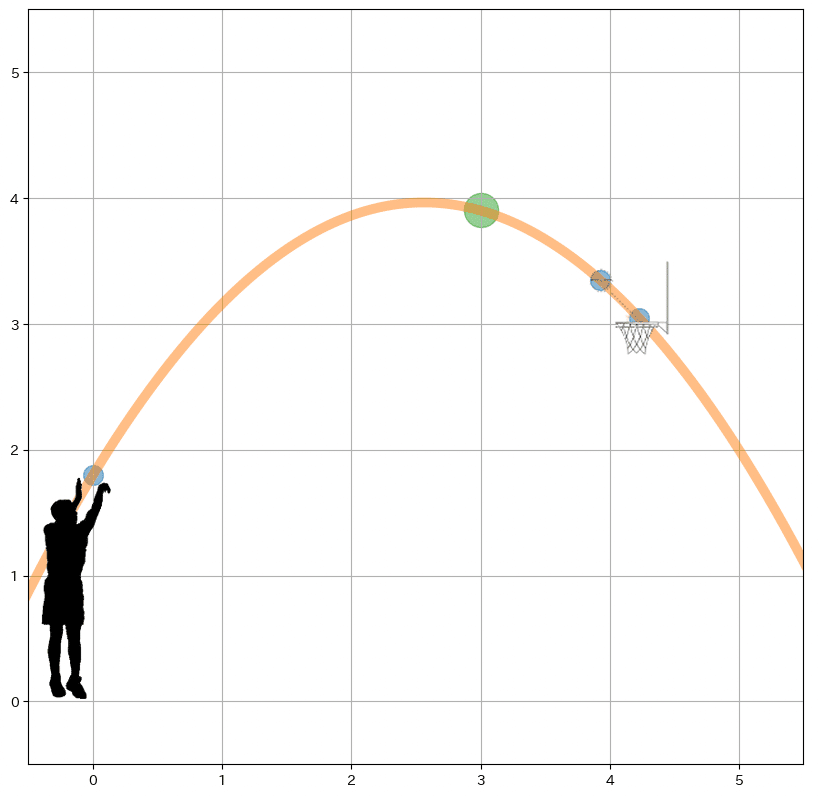

そして、ラスト、ゴールに入った絵も一応。笑


尚、撮影に際しては、1ショットずつ高さを確認しましたので、高さは正確かと思われます。
ただし、先程の説明の通り、ボールが若干小さい点は否めません。
また、カメラの歪みが人間の視覚と合致しているとも言い切れないかとは思います。
より分かりやすくするために、上記の画像を連結させてみました。

そして、以下gif動画作成も、トライをしてみました。
…が、こちらは少し弾道が低くなってしまいました…。
少し弾道が低い例として載せさせて頂きます…。💦
(何回か撮影したのですが、難しいですね…。😅
カメラの機能で、自動ピント調整も入ってしまっています…。)

さて、いかがでしたでしょうか?
比較的多くの方が、「思っていた以上に、ボールを高く放り上げる必要があるんだな…」という印象を受けたのではないでしょうか。
実際、私自身は、「思ったより高い!」という印象を受けました。
そして、その後、アーチを高くするように意識してみたところ、リングに弾かれることが少なくなった次第でした。
また、アーチを高くするように意識してから、swish(リングに当たらずにゴールが決まること)になる確率も上がり、練習時の気持ちよさも増した次第です。
以下、参考までの「one of the best swish!」となります。w

リングに弾かれる可能性が下がったことから、本検証を行う以前の私のシュートは、恐らく十分な高さのアーチを描けていなかったのだと思います。
つまり、アーチが低かった、或いは、ゴールに対するボールの入射角が浅かったものと思います。
繰り返しにはなり恐縮ですが、ゴールに対するボールの入射角が浅い場合、リングに弾かれる可能性は高くなる形となっています。
おわりに
ここまでの与太話に長々と付き合って下さった方、本当にありがとうございます…!!🙇
ひょっとしますと、バスケットボールが好きで、かつ、プログラムや統計などを把握している方でないと、難解といいますか、面白みが深くない内容となってしまったかもしれず…。💦
その点が大変恐縮といいますか、危惧しているところなのですが、少しでも楽しんで頂けたとしましたら、これ以上の喜びはありません。🙇
しかし、まあ、なんでしょう。
日頃行っている分析業務において行っている、以下のようなエクササイズが、このような形で私生活に功を奏すとは思ってもおりませんでした。w
- 先ず、事業ドメインについて調べてみる
- 目標を達成するに当たって、関連の成功前例を把握する
- 成功前例を、どう自分達に適用できるかを考察する
- 実際に検証を行い、実感を得る
恐らく、分析業務を行っている方は、これと同様のことを実施しているかと思います。
或いは、作業的/実務的に、抽象化と具体化、或いは、俯瞰と凝視を行った上で、上手くトレードオフを最適化しようとしたり、効率化を果たそうとしたりする形かと思います。
特にスポーツという、一朝一夕には想定の動作が再現できず、所望の結果までに相当量の練習を必要とするような課題である場合には、思考停止に陥らないようにトライ&エラーを行っていくことがコツであり、課題解決への近道になるのだと思われます。
(…と、それっぽいことを言って、結びにさせて頂こうかと思います…。🙇💦)
ちなみに、小職の実際のバスケの成長度合いについてですが、ミドルシュートが、打った本数の半数超程、成功するようになってきております。
いずれは、クリス・ポール選手のように、ドリブルからのプルアップジャンプミドルが、ほぼ100%に近い確率で決められるようになりたいと、淡い夢を抱いている次第です。
しかし、筋繊維の固い中年である為、怪我には特に気を付けながら、ほどほどに頑張りたいと思います…!💪