
ABC176の解答
ABC176の自分なりのアウトプットを書いていきます。
問題はこちらから。
https://atcoder.jp/contests/abc176/tasks
A Takoyaki
たこ焼きを焼く問題です。T分で一度にX個同時に焼けるたこ焼き器を持っています。N個焼くためには何分かかりますか。という問題。
基本は(N / X) と端数分の1を足したものににTを掛ければ良いのですが、N / Xが割り切れる場合に 端数が出ないため、ifで分岐させておきます。
という風に解きました。
しかし、他の解説を見ると、分岐のところは
ceil(N / X) ・・・切り上げ関数
とスマートに解いていたので真似します。
切り上げ関数は
(N + X - 1)/ X
で実現されます。実際に表を書いてみると商をX-1個ずらすと切り上げが実現されると思います。
#include <bits/stdc++.h>
#define rep(i,n) for(int i=0;i<n;i++)
using namespace std;
int main()
{
int n,x,t;
cin >> n >> x >> t;
int quo;
quo = (n+x-1) / x;
cout << quo * t;
return 0;
}B Multiple of 9
9の倍数かどうかを判定する問題です。
ただ、%9でやれば良いかと思いきや、入力が非常に大きいため文字列で処理します。
文字列を数値に変換するには「-'0'」としてあげます。
これは文字列も内部では数字で表現されていることを用いています。調べたところ文字の'0'は内部では数字の48と表現されているみたいです。もちろん'1'は内部では49となっています。そのため、'1'-'0'は49-48=1となり、文字列の1が数字に変換されるわけです。
あとは全部の桁を足して、9で割れるかを判定するだけですね。
#include <bits/stdc++.h>
#define rep(i,n) for(int i=0;i<n;i++)
using namespace std;
int main()
{
string str;
cin >> str;
int sum = 0;
while(1){
if(str.empty()) break;
char c = str[0];
int n = c - '0';
sum += n;
str.erase(0,1);
}
string ans;
if(sum%9 == 0) ans = "Yes";
else ans = "No";
cout << ans << endl;
return 0;
}桁が10^200000なので、すべてが9でも、桁の合計はintで収まります。そのため、都度sumを9で割る必要はありませんでしたね。
あと、私は足し算のところはwhileで書きましたが、
for(char c : s){
x += (c - '0');
}とするとさらにきれいに書けますね。
C Step
整列している人たちに前の人たちよりも身長が高くなるように台を設置してあげる問題。
これは、一番前の人から順に見ていって、前の人に足りない分の台を追加する。それを後ろまで素直にやれば答えが出ます。
愚直にやってますが、O(N)の計算量なので問題なく計算できます。
ただし、答えはintに収まらない可能性があるのことに注意します。
#include <bits/stdc++.h>
#define rep(i,n) for(int i=0;i<n;i++)
using namespace std;
using ll = long long;
int main()
{
int n;
cin >> n;
vector<int> a(n);
rep(i,n) cin >> a[i];
int max = 0;
ll sum = 0;
rep(i,n){
if(max > a[i]){
sum += max - a[i];
}
else max = a[i];
}
cout << sum << endl;
return 0;
}D Wizard in Maze
迷路に迷い込んだ魔法使いがゴールを目指す問題です。迷路には通路と壁があり、当然ですが壁は移動できません。移動方法は通路を通る「歩き」と近くの壁を飛び越えられる「ワープ」があります。さて、ゴールするにはワープを何回必要とするでしょうか。もしくは、ワープを使ってもゴールできないのでしょうか。
今回は、迷路の経路を解く際によく用いられる、幅優先探索(Breadth First Search : BFS)を用います。私自身も集積回路の経路を探索するという課題に取り組んだ際に深さ優先探索(Depth First Search : DFS)と比較して用いました。
BFSでは同じ深さのものを広げていくようなアルゴリズムで解となる最短経路を求めます。下記の迷路の最短経路を例にとります。(・:通路、#:壁)
・・・・・・
・・#・・#
・#・・・・
#・#・・・
スタートは左上です。まず、スタートに距離0を書きこみその上下左右(等距離のもの)を探索し距離1とします。
01・・・・
1・#・・#
・#・・・・
#・#・・・
次は1のものから探索していきます。という作業をゴールとなる右下が埋まるまで(今回は全コストが同じなため)行います。すでにコストが書き込まれている場合、移動後のコストと比較して小さい方を取ります。
012345
12#45#
2#6567
#・#678
ということで、8という答えが出ました。
このアルゴリズムをプログラムで表現することを考えます。
距離を書き込む2次元配列(Infで初期化)と座標を保持する容器を用います。まずスタートの座標(0,0)を容器に入れます。
{ }←(0,0)
当然ですが、容器は
{(0,0)}
となっています。次に容器の先頭から取り出していきます。(0,0)の次の座標は(0,1)(1,0)です。(0,1)(1,0)ともに距離はInfなので、それを1(現在地の0 +1)に書き換えます。書き換えをしたので、(0,1)(1,0)を容器に入れます。(書き換えない場合は入れません)
(0,0)←{ }←(0,1) (1,0)
次に先頭にある(0,1)を取り出して、その移動先(0,0) (0,2) (1,1)の書き換えをします。(0,0)はすでに0が書かれているため2では更新できません。そのため、次は(0,2) (1,0)を容器に入れます。
(0,1)←{(1,0)}←(0,2)(1,1)
こんな感じで、容器が空になるまで操作を繰り返せば答えが出ます。
ただし、今回は何回ワープを使いますかという問題なので、本手法を少し拡張します。上下左右の歩き移動のコストを0、ワープ移動(問題と同様に自分を中心とした5*5のマスへの移動とする)のコストを1とします。
まず(0,0)では歩きで(0,1)(1,0)に行けます。そして、ワープでは壁を除いて、(0,1)(0,2)(1,0)(1,1)(2,0)(2,2)に移動できます。重複してる点は歩きを優先します。
001・・・
01#・・#
1#1・・・
#・#・・・
更新した点を容器に入れるのですが、更新回数を減らすために歩き移動のものは前から、ワープ移動のものは後ろから入れていきます。
(0,0)← →(0,1) (1,0){ } ←(2,0)(1,1)(2,0)(2,2)
次に一番前にある(0,1)を取り出して操作します。
0001・・
00#1・#
1#11・・
#・#・・・
(0,1)← (2,0) (1,1)→ {(1,0) (2,0)(1,1)(2,0)(2,2)} ←(3,0)(3,1)(3,2)
この操作を容器が空になるまで行います。今回の例では閉路の(3,1)のみが1となり、残りは全部0になります。
000000
00#00#
0#0000
#1#000
アルゴリズムは以上です。以下実装です。
#include <bits/stdc++.h>
#define rep(i,n) for(int i=0;i<n;i++)
using namespace std;
using ll = long long;
using P = pair<int,int>;
int main()
{
int h, w, sh, sw, th, tw;
cin >> h >> w >> sh >> sw >> th >> tw;
--sh; --sw; --th; --tw;
vector<string> s(h);
//入力がh行のstring
rep(i,h) cin >> s[i];
vector<vector<int>> dist(h,vector<int>(w,INT_MAX));
deque<P> q;
vector<int> mx = {0, 0, -1, 1};
vector<int> my = {1, -1, 0, 0};
dist[sh][sw] = 0;
q.emplace_back(sh,sw);
while(!q.empty()){
int i = q[0].first;
int j = q[0].second;
int d = dist[i][j];
q.pop_front();
//歩きでの移動
rep(k,4){
int ni = i + mx[k];
int nj = j + my[k];
//枠外に飛び出さないかの判定
if(ni < 0 || h-1 < ni || nj < 0 || w-1 < nj) continue;
//壁かの判定
if(s[ni][nj] == '#') continue;
//更新可能、到達済みかの判定
if(dist[ni][nj] <= d) continue;
dist[ni][nj] = d;
q.emplace_front(ni,nj);
}
//魔法での移動
for(int wx = -2; wx <= 2; ++wx){
for(int wy = -2; wy <= 2; ++wy){
int ni = i + wx;
int nj = j + wy;
//枠外に飛び出さないかの判定
if(ni < 0 || h-1 < ni || nj < 0 || w-1 < nj) continue;
//壁かの判定
if(s[ni][nj] == '#') continue;
//更新可能、到達済みかの判定
if(dist[ni][nj] <= d+1) continue;
dist[ni][nj] = d+1;
q.emplace_back(ni,nj);
}
}
}
int ans = dist[th][tw];
if(ans == INT_MAX) ans = -1;
cout << ans << endl;
return 0;
}初めは容器に通常のvectorを用いていたのですが、TLEしてしまったので、dequeという構造を用いました。vectorとは確保するメモリ領域が異なるため、配列の先頭に要素を追加する操作を高速で行うことができます。
REになっちゃてますが、計算時間が1/10になりました。

E Bomber
某ボンバーマンのような問題です。h*wの盤面上にm個の爆弾があり、フルファイヤー状態の爆弾を一つ置いたときに、誘爆できる爆弾の最大値を求める問題。ただし、本家とは違って、元々置いてあった爆弾は誘爆しません。
私はスーパーファミコンの5が好きでした。5のキャラは4と異なりキャラによる特殊能力がないのですが、鉄仮面ボンバーを愛用してました。
本問題は取り掛かり易いと思います。設置した爆弾は上下左右に爆発するため、最も爆弾が多い列と行をそれぞれ求めて、その交点に爆弾を置けば、最も多くの爆弾を誘爆できます。
そして、誘爆できる個数は列の爆弾数と行の爆弾数の和になります。ただし、設置した場所に爆弾がある場合には、1つの爆弾を重複してカウントしてるため、和-1が答えとなります。
以上より、アルゴリズムとしては
1、行ごと、列ごとの爆弾数を数える。
2、その最大値をとる行列(複数存在する場合は全て)を抽出。
3、抽出した行列(全組み合わせ)に対し、設置場所に爆弾がない点を探す。
4、一つでも見つかれば行列の爆弾の和、見つからない場合和-1が解となる。
こんな感じです。以下実装です。
#include <bits/stdc++.h>
#define rep(i,n) for(int i=0;i<n;i++)
using namespace std;
using ll = long long;
using P = pair<int,int>;
int main()
{
int h, w, m;
cin >> h >> w >> m;
vector<int> bh(h);
vector<int> bw(w);
set<P> b;
rep(k,m){
int i, j;
cin >> i >> j;
--i, --j;
++bh[i], ++bw[j];
b.emplace(i,j);
}
int max_w = 0;
int max_h = 0;
rep(i,h) max_h = max(max_h,bh[i]);
rep(i,w) max_w = max(max_w,bw[i]);
vector<int> mh;
vector<int> mw;
rep(i,h){
if(max_h == bh[i]) mh.emplace_back(i);
}
rep(i,w){
if(max_w == bw[i]) mw.emplace_back(i);
}
int ans = max_w + max_h;
rep(i,mh.size()){
P mp;
mp.first = mh[i];
rep(j,mw.size()){
mp.second = mw[j];
//もし設置場所に爆弾があればcontinue
if(b.count(mp)) continue;
cout << ans << endl;
return 0;
}
}
cout << ans-1 << endl;
return 0;
}今回は爆弾のある場所の管理として初めはvectorを用いていたのですが、TLEのために、setというものに変更しました。countというメソッドにより、高速に要素の一致を検索することができます。D問題と同様に計算時間の比較を示しておきます。
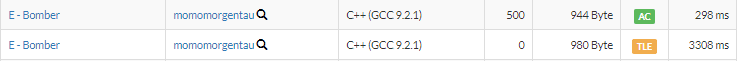
F Brave CHAIN
一列に並んだカードを取っていきスコアを最大化する問題。
1~nまでの数字が書かれたカードが3*n枚並んでいます。ただし、すべての数字が3枚含まれているとは限りません。残りのカードが3枚になるまで次の操作を行います。
左からカードを5枚とって、それを任意の順番に並び替える。その後左の3枚を列から取り除く。
このとき、取り除いた3枚の数字がすべて一致していたら1ポイントを獲得できます。さらに最後に残った3枚の数字がすべて一致していたら、同様に1ポイント獲得します。
まず、この問題をどのように考えるかです。
左から5枚並べ変えて、左から3枚取るという操作がありますが、結局のところ5枚から3枚を除き、2枚を残すという操作になります。次の施行では、残った2枚と次に並んだ3枚の合計5枚のうちから同様の操作を行います。
そのため現在の状態は、残った数字をa, b、次に並んだ数字をx, y, zとすると
数字 a が一番左にある。
数字 b が左から二番目にある。
カード列の i 番目まで並び替えた。
という3つのパラメータにより表すことが可能です。そのため、3次元の動的計画法を実装してあげれば解を求めることができます。
dp[i][a][b] : こんな感じです。
このとき、iは3ずつ変化していきます。
しかし、計算量はO(n^3)となるため、どうにかして計算量を削減する必要があります。
今回は、上記操作をしてテーブルを更新する際の場合分けを書いてあげることで削減していきます。その際に3次元であればどうなるかを参考程度に書いていきます。
a b x y zをどのように選択するかについて3つの場合に分けていきます。
i ) 新しい3枚(x, y, z)を除き、 a, bを残す場合。
この場合はとても簡単です。現在残っているカード(a, b)に関わらず、次の条件で得点を獲得できます。
x = y = z
a, bに関わらないというのがポイントで現在残っているすべてのa, bの組に関してそのスコアを+1してあげます。その後はa,bが残ります。
3次元であれば、
dp[i+3][a][b] = dp[i][a][b] + 1
です。ただし、すべてのa, bを更新するのは非常にコストがかかります。ii ) やiii )と同様に書くなら、
rep(ai, n)rep(bi,n) dp[i+3][ai][bi] = dp[i][ai][bi] + 1;
でO(n^2)です。
そのため、計算上の都合としてx = y = zが一致した回数を記憶する変数(プログラムではint ex)を用います。もし、一致したらテーブルは更新せずにexを+1、そしてx = y = zをなかったものとして考えます。そして最後に答えにexを加算すれば、この場合の操作が実現されます。
ii ) 新しい2枚(x, y)と古い1枚(a)を除く場合。
この場合が一番複雑です。iii )から読むと理解しやすいかもしれません。
この操作をすると、x, y, a が除かれ、z, bが残ります。
新しいカードがx = yとなっているときに得点を獲得できるチャンスがあります。
そのため、現在のaに関してfor文を回して a = xとなったらスコアを加算します。
rep(bi, n){
if(x == y) dp[i+3][z][bi] = dp[i][x][bi]+1;
}dp[i][a][b]のaの部分がx、つまり a = xの要素を更新します。この際に、bは問わないのですべてのbに関して更新します。
これで、x, y, aを除く場合が終わったので、y,z,a, z,x,aを除く場合も同様に考えてあげます。また、aとbは実装の際に順不同とするので、この3通りだけ考えます。
iii ) 新しい1枚(x)と古い1枚(a, b)を除く場合。
この操作をすると y, zが残ります。また、この操作で得点が獲得できるのは
a = b = x
の場合です。ii )とは違って、bは問わないなどの条件はないので、一回の更新で終わりです。
dp[i+3][y][z] = dp[i][x][x]+1;
dp[i][a][b]の aとbがxのときにテーブルを更新します。あとは、y, a, bとz, a, bも同様に考えてあげます。
上記の i ), ii ), iii )を実装するのですが、bは問わないという処理が複数登場するため、a の数字は含むがbは何でもいいよ(または、逆)、という際のスコアの最大値を保存しておく配列(プログラムでは maxa[2010])を用います。maxa[4]であったら、a, b に4を含むときの最大スコアが入ってます。さらに、a も bもなんでもいいよという場合の最大値を保存しておく変数(プログラムではmaxab)も用います。現在取りうる最大スコアが入っています。
dpのテーブルもこの変数にて更新をしていきます。
また、注意点として同じイテレータ内で条件分けして更新しているため、適宜更新をすると、計算が壊れます。(i ) ii ) iii )の順番を変えると、答えが変わる)それぞれの条件は更新後のi +3ではなく、更新前のi のパラメータで更新する必要があります。
そのため、更新に必要な要素(更新後のa, b, スコア)を保持して、すべての条件を見終わったら一気に更新をします。
実装です。
#include <bits/stdc++.h>
#define rep(i,n) for(int i=0;i<n;i++)
using namespace std;
using ll = long long;
using P = pair<int,int>;
using T = tuple<int,int,int>;
int a[6010];
int dp[2010][2010];
int maxa[2010]; //要素にiを持つ場合の最大値
int const inf = 1e9;
int main(){
int n;
cin >> n;
int n3 = n*3;
rep(i,n3) cin >> a[i],--a[i];
rep(i,n)rep(j,n) dp[i][j] = -inf;
rep(i,n) maxa[i] = -inf;
dp[a[0]][a[1]] = 0;
dp[a[1]][a[0]] = 0;
maxa[a[0]] = maxa[a[1]] = 0;
int maxab = 0; //その時点での最大値
int ex = 0;
for(int i=2; i < n3-2; i+=3){
int x = a[i];
int y = a[i+1];
int z = a[i+2];
//新しい3枚が一致していたとき
if(x == y && y == z){
++ex;
continue;
}
vector<T> upd;
rep(j,3){
//古い2枚と新しい1枚
//古いのを2枚捨てるからその時点の最大値maxabと比較。
int m = max(maxab, dp[z][z]+1);
upd.emplace_back(x,y,m);
//古い1枚と新しい2枚
//古いものを1枚捨てるから、捨てないほうを含む最大値maxa[k]と比較。
rep(k,n){
int m = maxa[k];
if(x == y) m = max(m, dp[x][k]+1);
upd.emplace_back(z,k,m);
}
swap(x,y); swap(y,z);
}
for(auto t : upd){
int na, nb, s;
tie(na, nb, s) = t;
dp[na][nb] = max(dp[na][nb], s);
dp[nb][na] = max(dp[nb][na], s);
//na,nbを含むテーブルの最大値を更新
maxa[na] = max(maxa[na], s);
maxa[nb] = max(maxa[nb], s);
maxab = max(maxab, s);
}
}
int ans = maxab;
//最後の要素が一致
int al = a[n3-1];
ans = max(ans, dp[al][al]+1);
//条件1を満たした回数
ans += ex;
cout << ans << endl;
return 0;
}以上です。公式と同様にx,y,zの組み合わせをswapにて実装したのですが、上記の通り
rep(i,3) 条件2, 条件3 swap(x,y) swap(y,z);
とするとacですが、
rep(i,3) 条件2 swap(x,y) swap(y,z);
rep(i,3) 条件3 swap(x,y) swap(y,z);
と分けて実装したら、いくつかのテストでwaとなりました。2つの違いが判らないため、有識者の方がいましたらご教授いただきたいです。
この記事が気に入ったらサポートをしてみませんか?
