
kaggleコンペ初挑戦!タイタニック号の生存予測で学んだ機械学習の基礎①
Kaggleに初めて参加する際、どのコンペに挑戦するか迷ってしまいますよね。
私が最初に選んだのは、多くの人が取り組む「タイタニック号の生存予測」コンペです。
このコンペでは、タイタニック号に乗船していた乗客の生存を予測するモデルを構築することが求められます。
ここでは、私が実装したモデルや前処理のプロセスを詳しく解説していきます。
実行環境
Windows11
Python3
Kaggle
分析の流れ

実装
まずは、最終的な完成コードです。
import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score
# 各ファイルを読み込み
train_df = pd.read_csv('/kaggle/input/titanic/train.csv')
test_df = pd.read_csv('/kaggle/input/titanic/test.csv')
sample_sub = pd.read_csv('/kaggle/input/titanic/gender_submission.csv')
# 訓練データとテストデータを結合しall_dfを作成
all_df = pd.concat([train_df,test_df],axis=0).reset_index(drop=True)
# 訓練データとテストデータを判定するためのカラムを作成
all_df['Test_Flag'] = 0
all_df.loc[train_df.shape[0]: , 'Test_Flag'] = 1
# Ageの欠損を中央値で補完
all_df['Age'] = all_df['Age'].fillna( all_df['Age'].median())
# Fareの欠損を中央値で補完
all_df['Fare'] = all_df['Fare'].fillna( all_df['Fare'].median())
# Embarkedの欠損を「'NaN'」で補完
all_df['Embarked'] = all_df['Embarked'].fillna('NaN')
# Fareを4つの区間に分類し、カテゴリカル変数に変換
all_df['FareBand'] = pd.qcut(all_df['Fare'], 4)
# Ageを4つの区間に分類し、カテゴリカル変数に変換
all_df['AgeBand'] = pd.qcut(all_df['Age'], 4)
# Sex、PclassをOne-Hot_Encodingで変換
all_df = pd.get_dummies(all_df, columns= ["Sex", "Pclass"],dtype='float')
# AgeBand, FareBand, EmbarkedをOne-Hot Encodingで変換
all_df = pd.get_dummies(all_df, columns=['AgeBand','FareBand','Embarked'],dtype='float')
# 前処理を施したall_dfを訓練データとテストデータに分割
train = all_df[all_df['Test_Flag']==0]
test = all_df[all_df['Test_Flag']==1].reset_index(drop=True)
target = train['Survived']
# 今回学習に用いないカラムを削除
drop_col = [
'PassengerId', 'Age',
'Ticket', 'Fare', 'Cabin',
'Test_Flag', 'Name', 'Survived'
]
train = train.drop(drop_col, axis=1)
test = test.drop(drop_col, axis=1)
# 訓練データの一部を検証データに分割
X_train ,X_val ,y_train ,y_val = train_test_split(
train, target,
test_size=0.2, shuffle=True,random_state=0
)
# モデルを定義し学習
model = LogisticRegression()
model.fit(X_train, y_train)
# 訓練データに対しての予測を行い、正答率を算出
y_pred = model.predict(X_train)
print(accuracy_score(y_train, y_pred))
# テストデータを予測 (1.3.5)
test_pred = model.predict(test)
# 予測結果をサブミットするファイル形式に変更
sample_sub["Survived"] = np.where(test_pred>=0.5, 1, 0)
display(sample_sub.head(10))
# 提出ファイルを出力
sample_sub.to_csv("submission.csv", index=False)それでは、流れに沿って詳しく解説していきます。
1.データの読み込み
import numpy as np
import pandas as pd
# 訓練データ読み込み
train_df = pd.read_csv("/kaggle/input/titanic/train.csv")
# テストデータ読み込み
test_df = pd.read_csv("/kaggle/input/titanic/test.csv")
# 提出データ読み込み
sample_sub = pd.read_csv("/kaggle/input/titanic/gender_submission.csv")2.データの確認
読み込んだデータを確認していきます。
# 訓練データの形状
print(f"train_df_shape : {train_df.shape}")
>>> 出力結果
train_df_shape : (891, 12)891人の乗客データと12列の乗客データがあります。
# 各columnのデータ型
print(f"{train_df.dtypes}")
>>> 出力結果
PassengerId int64
Survived int64
Pclass int64
Name object
Sex object
Age float64
SibSp int64
Parch int64
Ticket object
Fare float64
Cabin object
Embarked object
dtype: object整数(int), 小数(float), 文字(object)があります。
# 先頭3つを可視化
display(train_df.head(3)) # display:データフレームやその他の出力をより見やすく表示
>>> 出力結果
PassengerId Survived Pclass Name Sex Age SibSp Parch Ticket Fare Cabin Embarked
1 0 3 Braund, Mr. Owen Harris male 22.0 1 0 A/5 21171 7.2500 NaN S
2 1 1 Cumings, Mrs. John Bradley female 38.0 1 0 PC 17599 71.2833 C85 C
3 1 3 Heikkinen, Miss. Laina female 26.0 0 0 STON/O2.3101282 7.9250 NaN S各columnの意味は以下の通りです。
PassengerId : 乗客識別ユニークID
Survived : 1が生存、0が死亡 ← テストデータにおけるSurvivedを予測するのが本課題
Pclass : チケットのクラス、1st(上層)=1, 2nd(中級)=2, 3rd(下層)=3
Name : 乗客の名前
Sex : 男性(male), 女性(female)
Age : 年齢
SibSp : 同乗している兄弟、配偶者の人数
Parch : 同乗している両親、子供の数
Ticket : チケットの番号
Fare : 乗船料金
Cabin : 部屋番号
Embarked : 乗船した港(S=Southampton, C=Cherbourg, Q=Queenstown)
3.統計量の確認
まず、訓練データにおける数値データとカテゴリカルデータの統計量を確認します。
カテゴリカルデータは量的ではないデータで、ここではName, Sex, Ticket などがカテゴリカルデータです。
# 数値データの統計量を表示
display(train_df.describe())
>>> 出力結果
PassengerId Survived Pclass Age SibSp Parch Fare
count 891.000000 891.000000 891.000000 714.000000 891.000000 891.000000 891.000000
mean 446.000000 0.383838 2.308642 29.699118 0.523008 0.381594 32.204208
std 257.353842 0.486592 0.836071 14.526497 1.102743 0.806057 49.693429
min 1.000000 0.000000 1.000000 0.420000 0.000000 0.000000 0.000000
25% 223.500000 0.000000 2.000000 20.125000 0.000000 0.000000 7.910400
50% 446.000000 0.000000 3.000000 28.000000 0.000000 0.000000 14.454200
75% 668.500000 1.000000 3.000000 38.000000 1.000000 0.000000 31.000000
max 891.000000 1.000000 3.000000 80.000000 8.000000 6.000000 512.329200# カテゴリカルデータの統計量を表示
display(train_df.describe(exclude="number")) # exclude:除外
>>> 出力結果
Name Sex Ticket Cabin Embarked
count 891 891 891 204 889
unique 891 2 681 147 3
top Braund, Mr. Owen Harris male 347082 B96 B98 S
freq 1 577 7 4 644カテゴリカルデータの各統計量の意味は以下のとおりです。
count : データ数
unique : 種類の数
top : 最も多いデータ
freq : 頻度
算出した統計量から以下のようなことが確認できます。
countの項目から、Age, Cabin, Embarked のデータには、欠損値がある。
Survivedの平均が0.5より小さいので、目的変数であるSurvivedは偏りがあると判断。
Age, Fare の最大値が、平均値や中央値と比べて大きいので、外れ値があると予想。
SibSp, Parch の半分以上が0なので、同乗していた家族の人数には偏りがあると予想。
ここで、訓練データとテストデータを結合し、データ全体の統計量を算出します。
# 訓練データとテストデータを結合しall_dfを作成
all_df = pd.concat([train_df, test_df], axis=0).reset_index(drop=True)
# 訓練データとテストデータを判定するためのカラムを作成
all_df["Test_Flag"] = 0
all_df.loc[train_df.shape[0]: , "Test_Flag"] = 1
# データ全体における、数値データの統計量を表示
display(all_df.describe())
>>> 出力結果
PassengerId Survived Pclass Age SibSp Parch Fare Test_Flag
count 1309.000000 891.000000 1309.000000 1046.000000 1309.000000 1309.000000 1308.000000 1309.000000
mean 655.000000 0.383838 2.294882 29.881138 0.498854 0.385027 33.295479 0.319328
std 378.020061 0.486592 0.837836 14.413493 1.041658 0.865560 51.758668 0.466394
min 1.000000 0.000000 1.000000 0.170000 0.000000 0.000000 0.000000 0.000000
25% 328.000000 0.000000 2.000000 21.000000 0.000000 0.000000 7.895800 0.000000
50% 655.000000 0.000000 3.000000 28.000000 0.000000 0.000000 14.454200 0.000000
75% 982.000000 1.000000 3.000000 39.000000 1.000000 0.000000 31.275000 1.000000
max 1309.000000 1.000000 3.000000 80.000000 8.000000 9.000000 512.329200 1.000000# データ全体における、カテゴリカルデータの統計量を表示
display(all_df.describe(exclude="number"))
>>> 出力結果
Name Sex Ticket Cabin Embarked
count 1309 1309 1309 295 1307
unique 1307 2 929 186 3
top Connolly, Miss. Kate male CA. 2343 C23 C25 C27 S
freq 2 843 11 6 9144.重複の確認
訓練データとテストデータにおける、カテゴリカルデータの重複を確認します。
なぜ重複の確認をするのかというと、重複があまりにも少ないと、予測モデルは学習していない状況の予測を行うことになります。
すると、訓練データで見積もった予測性能とテストデータを予測した際の性能に乖離が生じてしまいます。
# Name, Pclass, Cabin の重複を確認
import matplotlib.pyplot as plt
from matplotlib_venn import venn2
# 「figsize=(8, 8)」図のサイズを指定、「ncols=3, nrows=1」3列1行のサブプロットが並んだ形
fig, axes = plt.subplots(figsize=(8, 8), ncols=3, nrows=1)
# zip関数は、複数のリストや配列を一度に処理
for col_name, ax in zip(["Name", "Pclass", "Cabin"], axes.ravel()): # ravel()多次元配列を1次元に変換
# 2つの集合をsubsetsという引数に渡して、Vennダイアグラムを作成
venn2(subsets=(set(train_df[col_name].unique()), set(test_df[col_name].unique())),
set_labels=("Train", "Test"),
ax=ax)
ax.set_title(col_name)
>>> 出力結果
# Sex, Ticket, Embarked の重複を確認
fig, axes = plt.subplots(figsize=(8, 8), ncols=3, nrows=1)
for col_name, ax in zip(["Sex", "Ticket", "Embarked"], axes.ravel()):
venn2(subsets=(set(train_df[col_name].unique()), set(test_df[col_name].unique())), # train_df, test_dfそれぞれの中で現在の列(col_name)のユニーク(unique)な値の集合(set)を作成
set_labels=("Train", "Test"),
ax=ax)
ax.set_title(col_name)
>>> 出力結果
5.データの可視化
まず可視化を通じて、偏りがないかなどを確認していきます。
# Survivedについて可視化
import seaborn as sns
sns.countplot(x="Survived", hue="Survived", data=train_df, legend=False) # hue:棒の色を値に応じて変える、legend:凡例
>>> 出力結果
生存者数より死亡者数の方が多いことがわかります。
# Sexについて可視化
sns.countplot(x="Sex", hue="Test_Flag", data=all_df)
>>> 出力結果
訓練データ(Test_Flag=0)、テストデータ(Test_Flag=1)におけるSexのグラフを見ると、男性の方が多く女性の方が少ないことがわかります。
# Ageについて可視化:Facetedグラフ(複数のサブプロットを持つグラフ)を作成
fig = sns.FacetGrid(all_df, col="Test_Flag", hue="Test_Flag", height=4)
fig.map(sns.histplot, "Age", bins=30, kde=False)
>>> 出力結果
# Fareについて可視化
fig = sns.FacetGrid(all_df, col="Test_Flag", hue="Test_Flag", height=4)
fig.map(sns.histplot, "Fare", bins=30, kde=False)
>>> 出力結果
Age, Fare の外れ値の有無について確認するために、ヒストグラムを用いて可視化しました。
その結果、Fareは大きく外れている値が訓練データとテストデータにあることがわかりました。
訓練データに外れ値が存在すると学習にその影響を与えます。
外れ値を含んで学習した結果、外れ値に対して上手く予測しても外れ値以外に対しては予測性能が下がり全体の正答率が下がる可能性があります。
次に、数値データの各変数間の相関をヒートマップで可視化します。
ヒートマップは数値を色の濃淡で表現するもので、一目で数字の大小が分かります。今回は、数値が1に近いと白色になり、-1に近いと黒色になります。
# 変数間の相関を可視化
sns.heatmap(train_df[["Survived", "Age", "SibSp", "Parch", "Fare"]].corr(),
vmax=1, vmin=-1, annot=True) # annot=True: Trueに設定することで、各セルに相関係数の値を表示
>>> 出力結果
SibSpとParchに正の弱い相関(0.41)が、SibSpとAgeに負の弱い相関(-0.31)があることが確認できました。
最後に、各カラムと目的変数 (Survived)の関係について可視化していきます。
# Sexについて可視化
sns.countplot(x="Sex", hue="Survived", data=train_df)
plt.show()
>>> 出力結果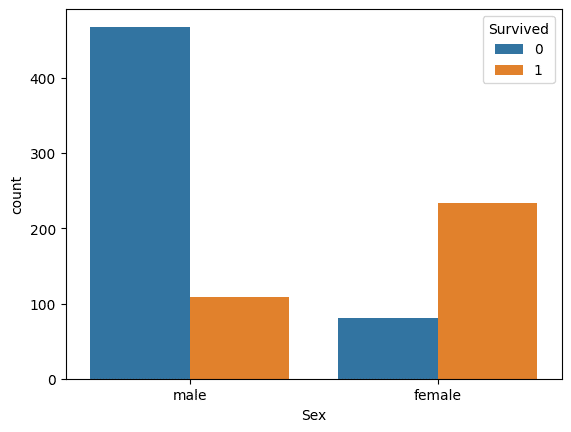
性別によって生存率に差があることがわかります。
# Pclassについて可視化
sns.countplot(x="Pclass", hue="Survived", data=train_df)
plt.show()
>>> 出力結果
チケットのクラスが大きくなるにつれて、生存率が小さくなっていることがわかります。
# Embarkedについて可視化
sns.countplot(x="Embarked", hue="Survived", data=train_df)
plt.show()
>>> 出力結果
乗船した港によって生存率に差があることがわかります。
# Ageについて可視化
fig = sns.FacetGrid(train_df, col="Survived", hue="Survived", height=4)
fig.map(sns.histplot, "Age", bins=30, kde=False)
>>> 出力結果
若い年齢(0歳から10歳程度)の人の生存率が高く、20~30代の生存率が低いことがわかります。
# Fareについて可視化
fig = sns.FacetGrid(train_df, col="Survived", hue="Survived", height=4)
fig.map(sns.histplot, "Fare", bins=25, kde=False)
>>> 出力結果
運賃が低い(Fareが0から100程度)乗客ほど、生存率が低いことがわかります。
# SibSpについて可視化
sns.countplot(x="SibSp", hue="Survived", data=train_df)
plt.show()
>>> 出力結果
同乗した兄弟、姉妹、配偶者の人数が1~2人の人の生存率が高いことがわかります。
# Parchについて可視化
sns.countplot(x="Parch", hue="Survived", data=train_df)
plt.show()
>>> 出力結果
同乗した親と子供の人数が、1~3人の人の生存率が高いことがわかります。
6.欠損値の補完
# Ageの欠損を中央値で補完
all_df["Age"] = all_df["Age"].fillna(all_df["Age"].median())
# Fareの欠損を中央値で補完
all_df["Fare"] = all_df["Fare"].fillna(all_df["Fare"].median())
# Embarkedの欠損を「'NaN'」で補完
all_df["Embarked"] = all_df["Embarked"].fillna("NaN")7.数値データのカテゴリカル変数化
外れ値が存在するとモデルの学習に悪影響を及ぼす可能性があります。
そこで数値データを特定の区間で分類し、カテゴリカル変数に変化させることにより、外れ値の影響を減らします。
# Fareを4つの区間に分類し、カテゴリカル変数に変換
all_df["FareBand"] = pd.qcut(all_df["Fare"], 4) # pd.qcut:データを等しい数のグループに分割
# Ageを4つの区間に分類し、カテゴリカル変数に変換
all_df["AgeBand"] = pd.qcut(all_df["Age"], 4)8.カテゴリカル変数の変換
カテゴリカル変数に対しOne-Hot Encodingを施し、モデルが扱えるよう変換していきます。
One-Hot Encodingとは、カテゴリーデータを機械学習モデルに使いやすい数値データに変換する方法です。
例えば、「赤」、「青」、「緑」の3つの色を考えると、それぞれを次のように表現します。
赤は[1, 0, 0]、青は[0, 1, 0]、緑は[0, 0, 1]です。
このように、各カテゴリをうまく表現することで、機械学習モデルがデータを数値的に扱えるようにします。
# Sex, Pclass, Embarked, AgeBand, FareBandをOne-Hot_Encodingで変換 (get_dummies:カテゴリ変数をダミー変数(0と1の数値に変換された列)に変換)
all_df = pd.get_dummies(all_df, columns=["Sex", "Pclass", "Embarked", "AgeBand", "FareBand"], dtype="float")9.テストデータの作成
特徴量作成が完了したので、次は予測モデルに学習させるために学習データとテストデータを作成します。
テストデータは、未知のデータと仮定し、予測モデルの学習時には使用せず、学習終了後に予測させ、評価指標で評価するために用います。
モデルを評価するために、ここではホールドアウト法を用います。
ホールドアウト法は、機械学習モデルの性能を評価するためのデータ分割方法です。
データを学習用とテスト用に分けて、モデルを学習用データで訓練し、テスト用データで精度を確認します。
この方法で、モデルが新しいデータに対してどれくらい正確に予測できるかを評価し、過学習(学習データに偏りすぎること)を防ぎます。
from sklearn.model_selection import train_test_split
# 前処理を施したall_dfを訓練データとテストデータに分割
train = all_df[all_df["Test_Flag"] == 0]
test = all_df[all_df["Test_Flag"] == 1].reset_index(drop=True)
# 訓練データのSurvivedをtargetにする
target = train["Survived"]
# 今回学習に用いないカラムを削除
drop_col = [
"PassengerId", "Age",
"Ticket", "Fare", "Cabin",
"Test_Flag", "Name", "Survived"
]
train = train.drop(drop_col, axis=1)
test = test.drop(drop_col, axis=1)
# 訓練データの一部を分割し検証データを作成
# 注意 :
# shuffleをTrueにするとランダムに分割されます。
# この時、random_stateを定義していないとモデルの再現性が取れなくなる。
X_train, X_val, y_train, y_val = train_test_split(train, target,
test_size=0.2, shuffle=True, random_state=0)10.モデルの学習と評価
今回は、ロジスティック回帰を用います。
ロジスティック回帰は、分類問題に使われる機械学習アルゴリズムです。
特に、二値分類(「合格か不合格か」など)で用いられ、入力データから得られる確率をもとに、結果がどちらかのクラスに分類されます。
モデルは、シグモイド関数を使って出力を0から1の範囲に変換し、一時値(通常は0.5)を基準にクラスを判別します。
簡単な仕組みで解釈がしやすく、例えば生存率や成功確率の予測に役立ちます。
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score
# モデルを定義し学習
model = LogisticRegression()
model.fit(X_train, y_train)
# 訓練データに対しての予測を行い、正答率を算出
y_pred = model.predict(X_train)
print(accuracy_score(y_train, y_pred))
>>> 出力結果
0.80056179775280911.ファイル作成とサブミット
作成した予測モデルを用いて、テストデータを予測し、結果をサブミット(提出)します。
# テストデータを予測
test_pred = model.predict(test)
# 予測結果をサブミットするファイル形式に変更
# np.where(...): NumPyの関数で、条件に基づいて値を置き換える
sample_sub["Survived"] = np.where(test_pred >= 0.5, 1, 0) # 生存確率が0.5以上の乗客を生存(1)、それ未満の乗客を非生存(0)としてフラグ付け
# 確認
display(sample_sub.head())
>>> 出力結果
PassengerId Survived
0 892 0
1 893 0
2 894 0
3 895 0
4 896 1# 提出ファイルを出力
sample_sub.to_csv("submission.csv", index=False)まとめ
以上が、Kaggleのタイタニック号の生存予測コンペで私が構築したモデルの流れです。
初挑戦ということで、シンプルなロジスティック回帰モデルを使用しましたが、スコアは0.77511となり、予想以上の結果となりました。
次回はより高度なモデルに挑戦し、さらなる精度向上を目指したいと思います。
