
比例代表の考察の現状と議席計算の結果
3月中は裏で進めている最高裁国民審査の分析が大きな負担となったため、特に成果を出せていませんでした。そこで今回はひとつ比例代表の考察について書いてみます。間をつなぐための記事ではありますが、選挙期間中の「押し込み」「押し負け」という現象について触れたので面白くはあると思います。現在のブロック別の議席計算の結果もあわせて示しました。
政党支持率を眺める
まず全国の政党支持率から始めましょう。次の図は、3月29日現在の政党支持率の平均です(3月22〜24日に実施された読売新聞と日経新聞の世論調査までを反映したものとなっています。各社の調査が一巡しているため、3月中に新たな発表はなさそうです)。一枚目が全政党を表示したもので、二枚目が10%未満の拡大です。

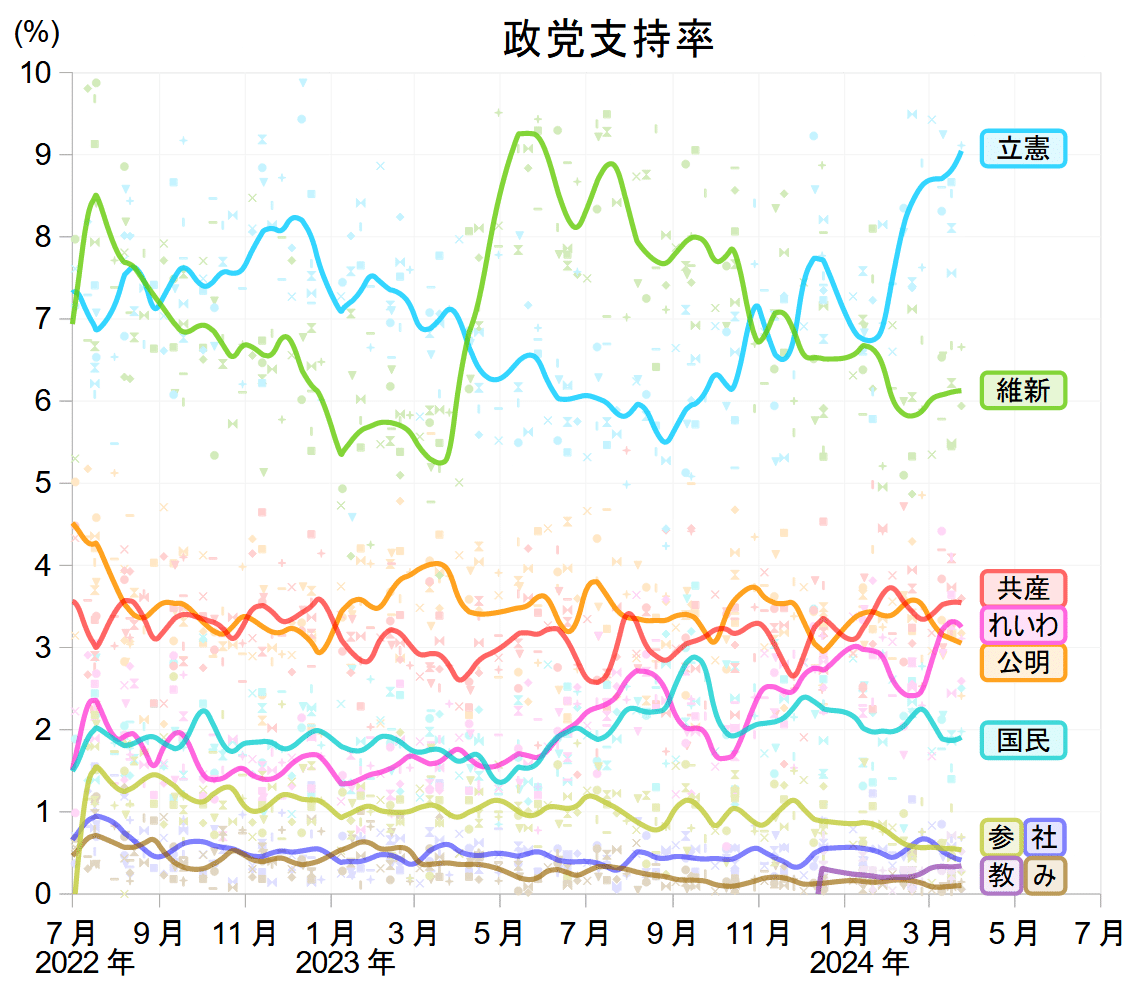
これらのグラフは、各社世論調査の固有の偏りを統計的に検出して補正し、様々なウエイトをかけて平均するという複雑なやり方で出しています。けれども実は、支持率の平均はどのようなやり方で出したところでほとんど変わりません。例えばひと月の間に10 社が一度ずつ調査をかけたとして、その結果を合計して10で割っても違いはほとんど生まれないのです。
具体的にNHK、読売・NNN(合同)、朝日、時事、共同、ANN、日経・テレ東(合同)、JNN、毎日、選挙ドットコム・JX通信(合同)が3月中に出した自民党の支持率を足して10で割ると24.46%となりますが、これは一枚目の図の最新の結果(24.95%)とほとんど一致することがお分かりになると思います。
それではなぜ複雑な計算をしているのかというと、その最大の目的は時間的な解像度を上げることにあります。ひと月の調査を足して10で割るやり方では、月々の支持率の動きしかわかりません。衆院選の公示から投開票までの12日間といった「一瞬」の間に何が起きているのかを知るためには、なるべく細かく日々の動きをとらえる必要があるわけです。
比例投票先
ところで各社の世論調査では、政党支持率のほかに、比例代表の投票先が聞かれることがあります。これについても現在の平均を示しました。

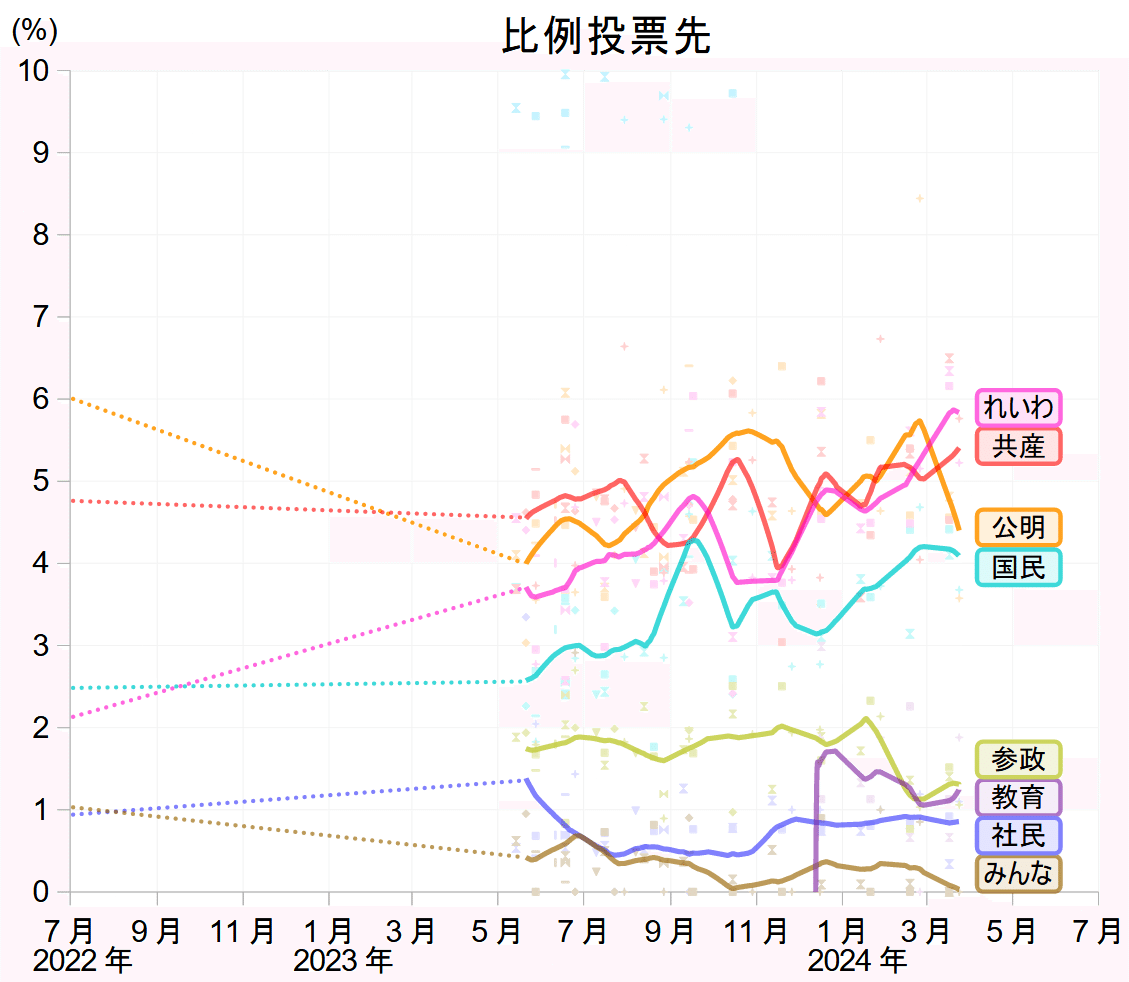
政党支持率からは、支持政党を持たない「無党派層」が次の選挙でどう振舞おうと考えているのかがわかりません。比例投票先はこの点に踏み込める長所を持っています。
他方で、比例投票先は各社が毎回聞くわけではないため、どうしても時間的な解像度が政党支持率に劣るのが弱点となります。
得票数の推定
そこで、ここでは比例代表の投票先を、政党支持率から直接推定する方法を試みてみましょう。

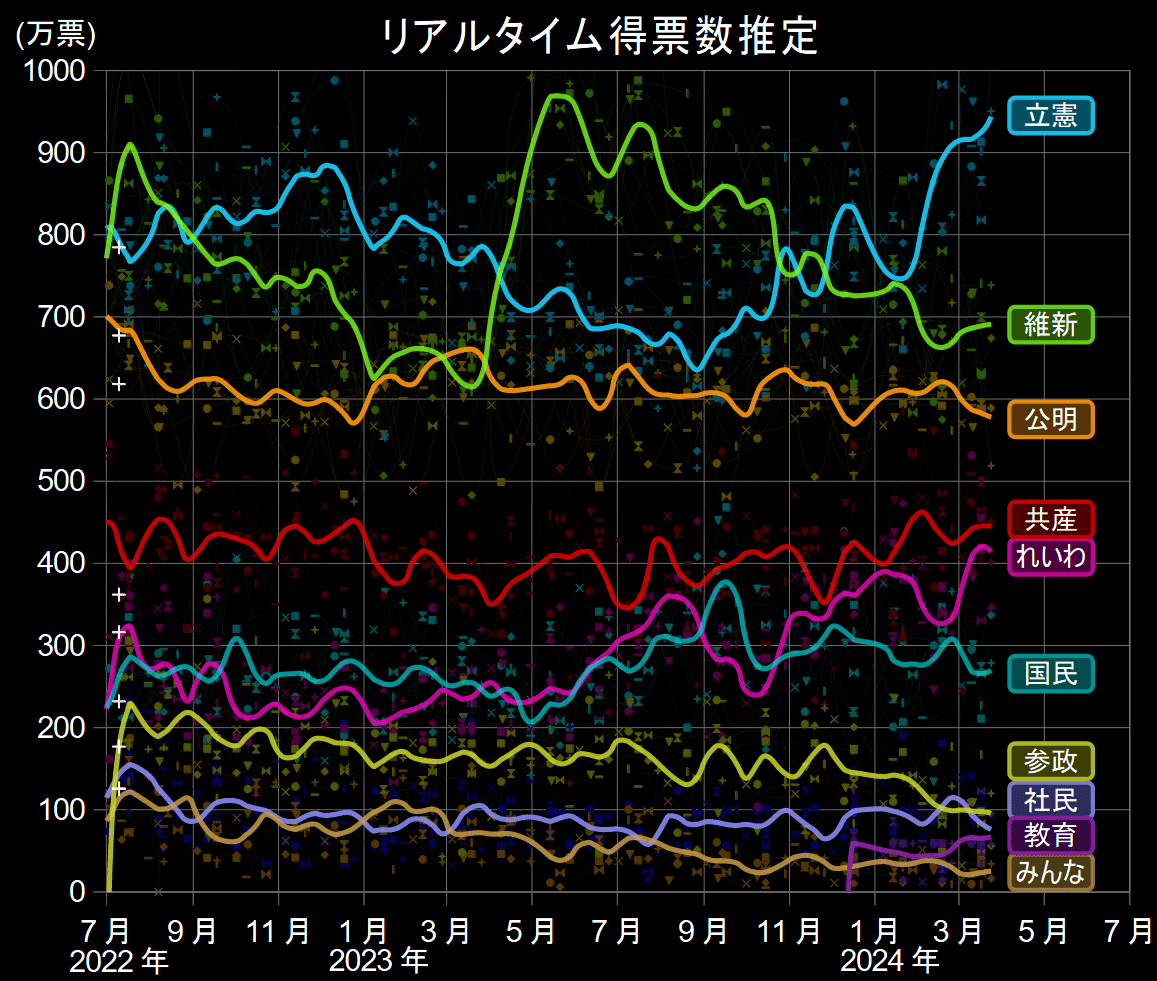
これは具体的には次の方法によっています。
①:2013年1月1日から2024年1月1日までの期間について、各社世論調査をもとに政党支持率を1日ごとに平均計算し、衆院選と参院選の投票日にあたる支持率を得る。
②:衆院選と参院選について、比例の絶対得票率を計算し、①で得た当日の支持率との関係を定める。
③:先に②で得た関係を用いて、日々の支持率を絶対得票率に換算する。
④:選挙管理委員会のデータと人口動態統計から、日々の有権者数を推定する。
⑤:最後に③と④を掛け算することにより、得票数を推定する。
これでどのくらい正しい結果が得られるのかは、後ほど一つ一つの政党について選挙結果との整合性を確認していきます。
3月29日現在の数字は次のとおりです。一票単位の精度が出るようなものではないですが、後で議席の計算に使うので記載しておきます。
自民 1526万8949票
立憲 943万9612票
維新 690万7666票
公明 577万7797票
共産 445万0391票
れいわ 414万1124票
国民 270万0245票
参政 95万7760票
社民 76万1931票
教育 66万9847票
みんな 25万3119票
この得票数の推定は、あくまで現在の支持率をもとに行ったものであることに注意してください。極端な言い方をすれば、これは即時投票――つまり「今日、選挙をやります。選挙運動の期間はありません。ただちに投票してください」というような無理のある数字となっています。実際は選挙期間中に支持率も変わるため、それにともなって票の推定も刻々と変化していくものとお考えください。
議席に換算すると
現在の得票数の推定をもとにして、衆院選の比例代表の議席を計算してみましょう。それには若干の仮定が必要です。というのも、衆院選の比例は全国が11のブロックに分割されており、各党がそれぞれのブロックで獲得した票にもとづいて議席が決められていくからです。

ここでは得票数が全国的に一律に変化すると考えます。つまり全国の票が前回選挙のR倍になった時、各ブロックの票もそれぞれ前回選挙のR倍になるものと仮定します。前回選挙としては第49回衆院選(2021年)を用いましたが、参政党は初めて国政に進出したのが2022年であるため、第26回参院選(2022年)の票をブロックごとに集計したものを用いました。
みんなでつくる党の計算には、そのまま第49回衆院選(2021年)のNHK党の票を用いました。また教育無償化を実現する会については、衆院選にも参院選にも臨んだことがないため、近畿ブロックの得票率が他のブロックの2倍になるとの仮定をおきました。このように仮定したのは所属する国会議員に近畿地方の人物が多いためですが、2倍という数字に根拠があるわけではありません。より近畿に票が集中すれば結果は変わりえます。
以上から各ブロックの票を次のように定めました。

議席計算の結果を示します。

この結果には違和感を覚えた方も少なくはないはずです。今の支持率で自民党は果たして64議席もとれるのでしょうか。共産党は14議席もとれるのでしょうか。その違和感は正しいもので、この数字にはぼく自身も賛同しない面があります。しかしどのように賛同しないのか、なぜこのような結果が出て、現実がどのようにずれるのかということを説明することが可能です。
すでに触れたように、この議席計算のもととなっている得票数の推定は現時点のものなのでした。つまり表2の結果は、選挙期間中の情勢の動きを考慮しないものとなっているわけです。
核心は相対得票率の動き
選挙期間中にどういったことが起こるのでしょうか。それには相対得票率の動きが重要となります。相対得票率とは「有効票のうち特定の政党が獲得した割合」で、マスコミなどで単に「得票率」と呼ばれるものと変わりません(正確を期して「相対」と書いているだけです)。
比例代表は限られた議席を各政党で分配するわけですから、票が伸びたとしても議席が増えるとは限りません。他の政党がより多く票を伸ばしていれば、議席は減ることになるからです。その票の割合を見る指標が相対得票率にほかなりません。
そこで、すでに示した得票数の推定を、相対得票率に換算したものを以下に示しました。


これら相対得票率の推定のグラフの増減は、得票数の推定のグラフ(図5と図6)とほとんど違いがありません。けれどもこれは、選挙期間中にはまったく別物といっていいような挙動を示すのです。
自民党
自民党を例にとって、2017年以降の衆院選と参院選2回ずつの動きを見てみましょう。図10が得票数の推定で、図11が相対得票率の推定のラインです。あわせて実際の選挙結果を白丸で示しました。


選挙時における2つの図の違いを見てください。自民党の相対得票率の推定は、選挙の直前に大きく下降していることがうかがえます。自民党がこのような下降のトレンドをもつのはどうしてなのでしょうか。
一般にそれぞれの政党の支持率には、衆院選や参院選の際に支持率が鋭く上がる現象(選挙ブースト)がみられます。しかし政権を担当する自民党の場合は普段からマスコミへの露出が多く、有権者への認知が広がりきっているため、選挙期間中に明確なブーストは見られません(図10)。それに対して野党への関心は解散後や公示後にはじめて上がるのでブーストが大きく、選挙期間中に自民党が押し負けて相対的に下降する(図11)のは自然なことといえるのです。
もっともこれは言葉として「押し負け」と言っているものの、自民党の選挙に勢いがないということを意味するわけではありません。普段から自民党の認知度が高いことは、自民党の支持率が選挙の実力と比べて常に過多の状態にあることを意味します(第一党効果)。対して野党への関心が選挙時に初めて伸びるということであれば、それは平時の野党の支持率が過小であることを意味します。おそらくそこにある世論調査のギャップが、選挙期間中に埋まっていく面があるのです。ここで行っているのはあくまで支持率をもとにした推定なので、そうしたことが自民党の「押し負け」としてあらわれているのでしょう。
しかしそういうことであれ、答えは明らかです。その押し負けが議席推定に反映できていなかったから、先ほどの表2において、自民党の議席が64という多い数字となったのです。ですからその64は上限の制約にあたると解釈することができるでしょう。
もしもただちに解散したならば、おそらく相対得票率は次のように推移するはずです。後に触れますが、この押し負けを考慮した計算結果は54議席でした。
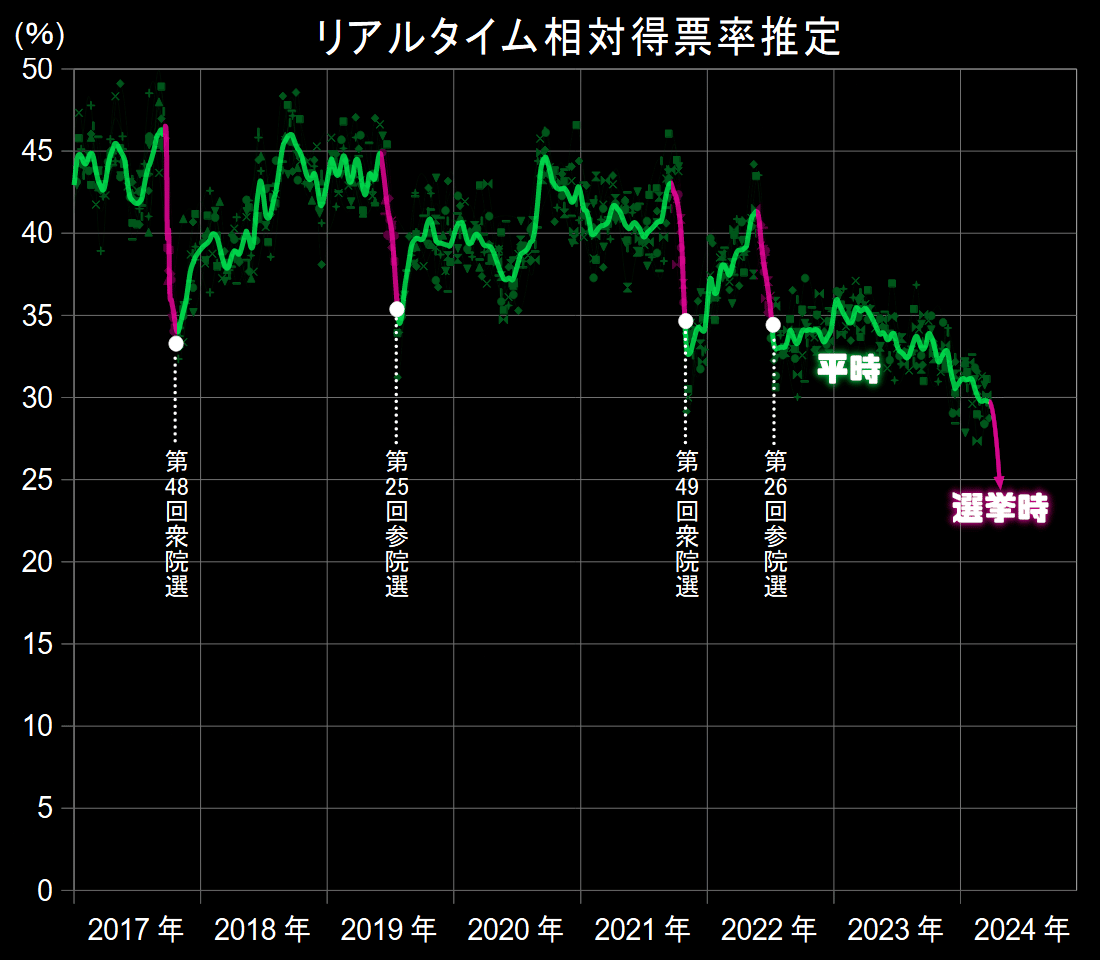
自民党に関しては、この選挙時の押し負けは強固なトレンドです。自民党は先の第49回衆院選(2021年)の直前に総裁選を行い、報道の注目を一手に集めることで、事実上、選挙を一か月先取りしたような運動をしました。しかしそれにともなう上昇は解散前に完結しており、解散後にはやはり押し負けが支配的になります。
自民党としては、そうなる前に支持率を上げなければ非常に不利になるわけです。ですから選挙分析の方面からいえば、解散するならそのための手を打ってからという論理にならないとおかしいといえます。自民党は必ず解散前に様々な手を打つと思います。
公明党
次に公明党を見てみましょう。ここでも2枚の図の違いに注目してください。


公明党は選挙ブーストをもつ政党です(図13)。しかし相対得票率で見る場合、ブーストが小さければ押し負けることを結果します(図14)。
この押し負けの原因としては、公明党の支持層が創価学会を基礎とする固いものであることが挙げられるかもしれません。つまり、普段から世論調査で堅実に支持層がとらえられるので、選挙期間中にワーッとのびることがないということです。これは後に共産党にも似た傾向があることを見ていきます。
というあたりで前半を終えさせてください。後半では、野党各党をひとつづつ見ていきます。また、ブロックごとのドント式の計算の結果と、その解釈について書きました。
みちしるべでは様々なデータの検討を通じて、今の社会はどのように見えるのか、何をすれば変わるのかといったことを模索していきます。今後も様々な発見を共有できるように頑張っていくので、参加してもらえたらとてもうれしいです。
