見出し画像

多数決って正しいの？～陪審定理とは？～

NPO法人 Mielka

はじめに

みなさん、突然ですが多数決は使ったことありますか？多数決は学園祭の出し物決めから選挙にまで非常に多くの場面で使われています。なぜこんなにも多くの場面で多数決が用いられているのでしょうか。多数決による結果はみんなにとってよいものなのでしょうか。この疑問に一定の示唆を与えてくれるのがこれから紹介する「陪審定理」というものです。

陪審定理とは

では早速本題に入りましょう。まず簡単に説明すると、陪審定理とは「ある限られた条件下での多数決の妥当性を数学的に示した定理」であり常に成り立つものではないことに注意してください。では陪審定理の説明に入ります。はじめに大きなはてなが浮かぶかもしれませんが安心してください。後に詳しくわかりやすく説明します。

陪審定理
片方の選択肢が正解である二者択一の問題について、次の条件を満たすとき有権者の数が多くなるにつれて多数決の判断が正しい確率は大きくなり1に近づく。また、有権者が3人以上の多数決による判断が正しい確率は常に1人による判断が正しい確率よりも大きい。

条件１：1人の有権者が正しく判断できる確率は50％より大きい
条件２：有権者は互いに独立に投票する。

少しかみ砕いてみましょう。まず陪審定理が使えるのは、○×問題のような選択肢が正解と不正解しかない2択の問題のみです。次に条件1は、有権者は少なくともコインの表裏で選ぶよりも正しい選択ができる、というもので条件2は、有権者は空気に流されたり、他人に判断を強制されたりしない、というものです。この条件が満たされていれば、①有権者が増えれば増えるほど多数決での判断が正しい確率が高まる ②3人以上の多数決は1人で決めるよりも正解を選べる確率が高い ということを示すのが陪審定理です。

この定理の詳しい数学的説明は本記事最後の補足に譲りますが、直観的には以下のようになります。まず当たり前ですが、1人だけで正しく判断できるのはその1人が正しい時だけです。しかし3人であれば、3人中2人が正しければ多数決の結果は正しくなります。このハードルは有権者の数を増やすとさらに下がり、例えば9人であればそのうち5人だけでも正しければ多数決の結果は正しくなります。101人であればほぼ半数の51人さえ正しく判断できれば、多数決で正しく判断できてしまいます。

もう少し具体的にみてみましょう。有権者は3人（Aさん、Bさん、Cさん）でこの3人が正しく判断できる確率は60％としましょう。このときの多数決の結果は8パターンあります。

  1. 3人とも間違える。

  2. A・Bが間違えて、Cが正解する。

  3. B・Cが間違えて、Aが正解する。

  4. A・Cが間違えて、Bが正解する。

  5. Aが間違えて、B・Cが正解する。

  6. Bが間違えて、A・Cが正解する。

  7. Cが間違えて、A・Bが正解する。

  8. 3人とも正解する

（表では、〇が正解を×が間違いを表します。確率はそのパターンが発生する確率を表してます。例えばパターン4ではAさんが間違えて（40％）Bさんが正解し（60％）Cさんが間違える（40％）確率を示しています。）

この8パターンのうち、多数決で正解を選べるのは、〇が過半数である5~8パターン目であり、その確率は 14.4＋14.4＋14.4＋21.6＝64.8％ です。

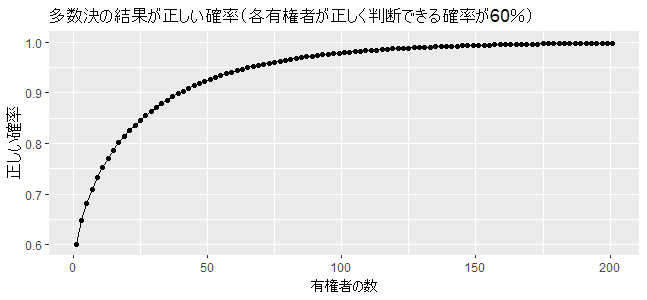
3人の多数決で正しく判断できる確率が64.8％であれば、1人で正しく判断できる確率である60％と大差ないように思えるかもしれません。しかし、重要なのは多数決で決めた方が確率が大きくなることです。そして、有権者の数を増やすと多数決で正しく判断できる確率はどんどんと大きくなります。例えば、7人で多数決を行えばその確率は70％を超え、101人であれば97％に達します（図1参照）。

　　（図１）

陪審定理の意義

この定理から、二者択一の問題に関しては多数決を取った方がより良い結果が得られるということが言えます。また、仮に有権者が正しく判断できる確率が51％のようにほんの少し50％を超えるだけだとしても、有権者の数が十分多ければ正解を判断できる確率はかなり高いものになります。もちろん有権者の数を増やして正解を判断できる確率が70％となったとしても、30％の確率で不正解を選んでしまうこともあるのですが、一人による判断よりもその確率は小さくなっています。これらのことは多数決による決定にかなりの正当性を与えています。

陪審定理の限界

陪審定理はただ多数決を正当化するものではありません。まずこの陪審定理は二者択一の問にしか適用できません。しかしながら現実には選挙も含めてそのような単純な問題はほぼ存在しません。また、条件2（有権者は互いに独立に投票する）も現実にはほとんどの場合成り立ちません。どんな多数決であれ、空気に流されたり、例えば上司などに判断を強制されたりすることはあるでしょう。また選挙に限って言えば、所属組織に半ば強制される組織票などがそれに該当します。さらに条件1（1人の有権者が正しく判断できる確率は50％より大きい）も成り立つかどうかは疑わしいところです。特に現代ではいたるところにフェイクニュースが転がっています。そのような中、本当に投票した人全員がコイントスで選ぶ以上に正解を選ぶことができるかには大きな疑問符が残ります。最後にそもそも何が「正解」なのかという問題があります。陪審定理の中では社会全体の利益を最大化させる選択肢を「正解」としています。しかし現実はそうではなく、多くの場合私たちは自己利益が最大になるものを正解とみなしがちです。

まとめ

以上、陪審定理についてみてきました。上で述べたように、陪審定理が現実に適用できる場面はそれほど多くないかもしれません。しかしながらこの定理は理論的な意思決定に関する議論への出発点になります。今後は選択肢が3つ以上ある場合についての記事も投稿予定ですのでご期待ください。最後に注意したいのが、陪審定理の濫用は全く不毛な議論を招きかねないということです。この定理をもとに多数決を礼賛したり、はたまた完全否定したりするようなことはぜひとも避けていただきたいものです。

参考文献・読書案内

この記事は次の2冊を参考に書きました。

「多数決を疑う　社会的選択理論とは何か」坂井豊貴　岩波書店
https://www.iwanami.co.jp/book/b226328.html

「社会的選択理論への招待ー投票と多数決の科学ー」坂井豊貴　日本評論社
https://nippyo.co.jp/shop/book/6371.html

本記事に興味を持ってくれた方にはまず一冊目「多数決を疑う」を強くお勧めします。この本は高校国語の教科書に掲載されるなど、非常に高く評価されています。（大修館書店、論理国語https://www.taishukan.co.jp/kokugo/product/?type=textbook&id=63）

また、より数学的な証明などを知りたいという方には「社会的選択理論への招待」を読んでみると良いでしょう。内容的には少し「多数決を疑う」よりも難しいものになっています。

記事の補足と数学的説明

  • 記事の補足

※1 「陪審定理とは」の中の「有権者が増えれば増えるほど多数決での判断が正しい確率が高まる」という説明について

有権者が偶数と奇数での場合分けがあるので、正確には「3人の多数決よりも5人、5人よりも7人・・・のほうが正しく判断できる確率は高い（偶数も同様）」であり、例えば6人による多数決の正しく判断できる確率は5人による多数決の正しく判断できる確率よりも低くなってます。また、図１は有権者が奇数の場合をプロットしてます。

※2 図1は以下の数式を統計ソフトRでプロット

最初のΣは、過半数以上の場合をすべての足し合わせを意味しています。例えば n=7 であれば、正解を判断できたのが4人、5人、6人、7人のときのそれぞれの確率を足し合わせています。

  • 数学的説明

数学の素養がある方向けに少し発展的な陪審定理の説明を載せておきます。ただ、いずれも厳密な証明は参考文献「社会的選択理論への招待ー投票と多数決の科学ー」を参照していただきたいです。

※1「有権者の数が多くなるにつれて多数決の判断が正しい確率は大きくなり1に近づく」について
　　　　　　　　　　　　　　　　　　　　　　　　　
大数の法則の応用です。直観的な説明になってしまいますが、有権者を無限人に増やせば有権者が正しく判断できる確率と全有権者の中で正解を選べた有権者の割合が一致します。そしてこれは0.5よりも大きいので過半数を獲得し必ず正解を選べます。

※2「有権者が3人以上の多数決による判断が正しい確率は常に1人による判断が正しい確率よりも大きい」について　　　　　　　　　　　　　　　　　　　　　　　　　　

3人による多数決と1人による判断を比べてみましょう。各有権者が正しく判断できる確率を$${p(0.5}$$$${<}$$$${p<1)}$$とすると、示したいのは次の式です。

$${p^3 + 3C2 p^2 (1-p)^1>p}$$

左辺は、3人ともが正しく判断できる確率（$${p^3}$$）と3人のうち2人が正解する確率｛$${3C2p^2(1-p)^1}$$｝を足したもので、右辺は1人による判断が正しい確率です。$${y＝（左辺）-（右辺）}$$とすると、

$${y=（左辺）-（右辺）}$$
$${  =p^3+3C2p^2(1-p)^1-p}$$
$${  =p^3+3p^2-3p^3-p}$$
$${  =-2p^3+3p^2-p}$$
$${  =-p(2p^2-3p+1)}$$
$${  =-p(2p-1)(p-1)}$$

$${0.5}$$$${<}$$$${p<1}$$  なので、$${y>0}$$  つまり   $${p^3+3C2p^2(1-p)^1>p}$$

したがって、3人による多数決が正しく判断できる確率が1人で正しく判断できる確率よりも大きくなることが分かりました。

また、有権者の数が大きくなるほど多数決で正しく判断できる確率も大きくなるので「有権者が3人以上の多数決による判断が正しい確率は常に1人による判断が正しい確率よりも大きい」ことがわかります。

繰り返しになりますが、厳密な証明は参考文献「社会的選択理論への招待ー投票と多数決の科学ー」を参照していただきたいです。

この記事が気に入ったらサポートをしてみませんか？