流体力学　薄翼の理論（その2）

　皆様おはこんばんちは。

　最近，流体力学を再度学び直してみようと思い，記事にしています。

　今回は，第66回目として「薄翼の理論（その2）」について紹介します。また，補足編の「薄翼理論の数学」で薄翼理論を勉強するためだけに必要な数学を取り上げております。尚，薄翼理論の2次元翼モデル，揚力Lと揚力係数CLについては，別記事で取り上げております。

（1）薄翼の影響因子

　はじめに，薄翼の理論と題していますが，薄翼に影響を及ぼす影響因子を以下に4つ紹介します（式（1）～（4）参照）。

この4つの影響因子（揚力L，揚力係数CL，前縁周りのモーメントM，モーメント係数CM）を急に紹介されてもよくわからないと思いますので，本記事ではこの4式を1つずつ証明していきます。前回は，揚力Lと揚力係数CLの2つを証明したので，今回は「前縁周りのモーメントM，モーメント係数CM」の2つを証明します。

（2）モーメントMの証明

　では，前縁周りのモーメントMを導出してみましょう。モーメントMは，以前取り上げたブラジウスの第2公式ではなく，クッタ・ジューコフスキーの定理（クッタ・ジューコフスキーの定理の式（1），（7）参照）を使用していきます。本来は，揚力Lを求めるものですが，これに距離xを乗算することでモーメントMを求める方針です。

まずは，ジューコフスキーの仮定を適用したxとθの関数（薄翼の理論の式（5）参照）からです。最終的にモーメントMは渦分布を積分することで導出するので，xについて微分しておきます。

次に，クッタ・ジューコフスキーの定理を使用して導出してみます。

ここで注意するべきは，積分するときにxの範囲からθの範囲に切り替えるため，定積分の範囲が変わることでしょうか。クッタ・ジューコフスキーの定理にジューコフスキーの仮定，渦分布を代入し，途中で加法定理を適用すると，式（5）となり，式（3）で示した前縁周りのモーメントMと同様になります。 

（3）モーメント係数CMの証明

　次に，薄翼理論のモーメント係数CMを導出してみましょう。モーメント係数CMは，以前取り上げた揚力Ｌ，抗力Dの定義式（翼理論の式（1）参照）をモーメントMに変換したものを使用していきます。

先ほど導出した前縁周りのモーメントM（式（5））とモーメントMの定義式は同じであることからお互いに同値と見なせます。この性質を使って以下のように計算すると，式（6）のようになり，式（4）で示した薄翼理論のモーメント係数CMと同様になります。

 

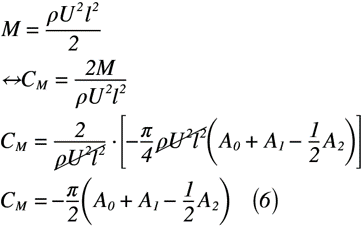
（4）まとめ

今回の記事のまとめを以下に示します。
①     前縁周りのモーメントMは，揚力Lと同様にクッタ・ジューコフスキーの定理からフーリエ級数で表した渦分布，ジューコフスキーの仮定を使うことで導出できる。
②     薄翼理論のモーメント係数CMは，前縁周りのモーメントMと揚力Ｌ,抗力Dの定義式をモーメントMに変換したものが同じであることを使うことで導出できる。

以上です。最後まで閲覧頂きありがとうございました。
次回は，「薄翼の理論（その3）」を取り上げる予定です。