流体力学　有限幅の翼

　皆様おはこんばんちは。
 
　最近，流体力学を再度学び直してみようと思い，記事にしています。
　今回は，第64回目として「有限幅の翼」について紹介したいと思います。今回は，翼の定量評価で使用する各因子（誘導抗力係数，揚力係数と迎え角の関係の2つ）を紹介していきます。

（1）誘導抗力係数CDi

　はじめに，誘導抗力係数CDiを導出してみましょう。ちなみに，誘導抗力Diとは，翼の上面と下面で圧力が異なる流体が流れること（圧力差）によって，「翼両端に一対の渦によって生じる抗力」のことです。図1のように翼幅に沿って無数の自由渦が生じます。
この自由渦は不安定な挙動を示すため，図1のように翼の後方で次第に巻き込まれて1対の自由渦になります。このような翼の後方で下方に向かう速度を誘導速度vと言います。

図1　翼周りの一対の渦の概略図

　先ほど誘導速度vを上手く用いて，翼の揚力Lを求めるために運動量保存側を使ったものを式（1）に示します。

ここで，m：流体質量流量，k：比例係数，ρ：流体密度，b：翼幅，u0：一様流れの流速を示します。k：比例係数は，理論上k=π/4となることを利用すると，式（2）のようになります。（等周定理 (isoperimetric problem)：表面積と体積に関する幾何学的関係が関与していますが，筆者にはよくわかりませんでした…）

翼の揚力Lは，別の方法で求めることもできます。求める方法は過去の記事を参照していただくことにして，式（3）に翼の揚力Lの定義式を示します。

2つの方法で翼の揚力Lを求められるということは，式（2）と式（3）は同値と見なすことができます。（中学校時代にやった連立方程式の「代入法」に相当します。）よって，計算を進めると，誘導速度vを式（4）のように求めることができます。

運動量保存側が成立するときの誘導速度vが求められると，次にできることはエネルギー保存側を使うことです。すなわち，運動エネルギーEkの定義式に沿って求めると，式（5）のようになります。

また，翼の下方に向かう流体の持つエネルギーは翼が進むたびに失うことになるので，これは誘導抗力Diと一様流れの流速u0の積は運動エネルギーと等しくなる仕事量となります。よって，エネルギー保存則が成立するので，式（6）のようになり，誘導抗力Diを求めることができます。

翼の誘導抗力Dは，別の方法で求めることもできます。求める方法は過去の記事を参照していただくことにして，式（7）に翼の誘導抗力Diの定義式を示します。

2つの方法で翼の誘導抗力Diを求められるということは，式（6）と式（7）は同値と見なすことができます。また，誘導速度v（式（4））も式（6）へ代入すると，誘導抗力係数CDiは，式（8）のように求められます。

ここで，b：翼幅，l：翼長の積で翼の面積Sを求められます。この関係を利用し，翼の寸法比λを式（9）のように定義します。

よって，得られた翼の寸法比λ（式（9））を式（8）へ代入すると，式（10）のようになり，最終的に求めたい誘導抗力係数CDiを導出できました。

（2）揚力係数CLと迎え角α0の関係（平板翼）

　次に，平板翼の揚力係数CLと迎え角α0の関係を導出してみましょう。図2に有限幅の翼の迎え角の概略図を示します。

図2　有限幅の翼の迎え角の概略図

重要なことは「誘導速度v」です。翼から十分前方の下向きの誘導速度は「0」になります。一方で，翼から十分後方の下向きの誘導速度は「v」となるため，翼付近の誘導速度は「v/2」として考えることにします。よって，2次元翼の迎え角α0は式（11）のようになります。

ここで，αl：有限幅の翼の迎え角，δ：x，y方向の速度における角度を示します。三角関数の定義に戻ってδを考えると，式（12）のようになります。強引ですが，tanδは値がゼロに近くなると，限りなくδの値と同じになるという近似を利用しています。

ここで，誘導速度v（式（4））を式（12）に代入すると，式（13）のようになります。

では，平板翼の揚力係数CLを導出するために，平板翼の揚力Lを求めます。翼の揚力Lの定義式（14）と平板翼の揚力L（式（15））となります。ちなみに，平板翼の揚力L（式（15））の導出根拠については過去の記事を参照してください。

2つの方法で翼の揚力Lを求められるということは，式（14）と式（15）は同値と見なすことができます。よって，平板翼の揚力係数CLは式（16）のように求めることができます。

ここで，式（13）と式（16）を式（11）に代入すると，式（17）のように2次元翼の迎え角α0と平板翼の揚力係数CLの関係式が求められます。

つまり，翼の寸法比λと平板翼の揚力係数CLが決まることで2次元翼の迎え角α0がわかるということになります。
 

（3）揚力係数CLと迎え角α0の関係（円弧翼）

　次に，円弧翼（そりのある翼）の揚力係数CLと迎え角α0の関係を導出してみましょう。平板翼と変わるのは，円弧翼の揚力Lです。円弧翼の揚力Lは式（18）のようになり，導出根拠については過去の記事を参照してください。

2つの方法で翼の揚力Lを求められるということは，式（14）と式（18）は同値と見なすことができます。よって，平板翼の揚力係数CLは式（19）のように求めることができます。

ここで，式（13）と式（19）を式（11）に代入すると，式（20）のように2次元翼の迎え角α0と平板翼の揚力係数CLの関係式が求められます。

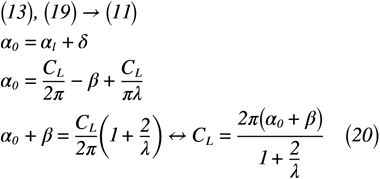
このように，2次元翼の迎え角α0と平板翼の揚力係数CLの関係は数多くの実験によって結果が得られています。
 

（4）まとめ

 今回の記事のまとめを以下に示します。
①     誘導抗力係数CDiは，誘導速度vを使って，2次元翼の運動量保存側とエネルギー保存則に基づいて算出され，揚力係数CLの2乗比例し，翼の寸法比λに反比例する関係式が得られる。
②     平板翼および円弧翼の迎え角α0は，揚力係数CLに比例し，翼の寸法比λに反比例する関係式が得られ，実験によって揚力係数CLと迎え角α0の関係が数多く検証されている。

以上です。最後まで閲覧頂きありがとうございました。
次回は，「薄翼の理論」について取り上げます。