流体力学　わき出しと吸込みのグラフ

　皆様おはこんばんちは。そして，お疲れ様です。

　最近，流体力学を再度学び直してみようと思い，記事にしています。
　第１３回目は，第１２回目で予告した通り，「わき出しと吸込みのグラフ」について紹介していきます。

（１）綺麗なグラフから自分で描けるグラフへ

　さて，前回取り上げた「わき出しと吸込み」の続きで「グラフ」について取り上げていきます。前回の「わき出しと吸込み」の参考となるグラフを図１，図2にそれぞれ示します。

図１　2次元流れのわき出し

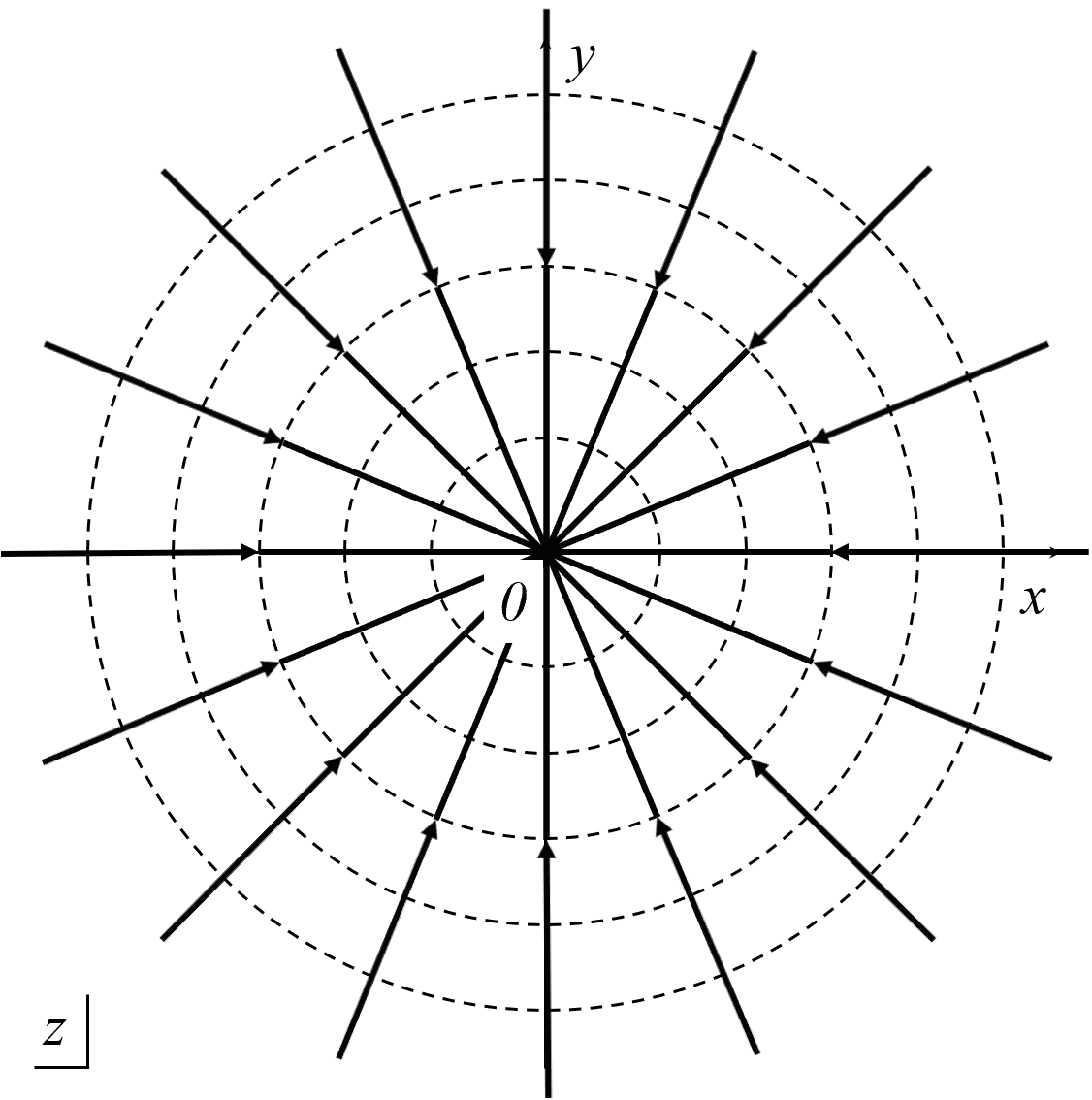
図２　2次元流れの吸込み

　図がいわゆる教科書的なグラフ，いわゆる綺麗なグラフです。グラフを覚えることを筆者は頑固拒否していますが，グラフを描くには綺麗な必要もありません。但し，かき方が分からなければどうしようもありません。
　以前に「一様流れのグラフ」を取り扱いましたが，直交座標に描くだけでした。つまり，多くの方々が中学・高校までやってきたグラフの書き方と変わりませんでした。
　今回取り上げる「わき出しと吸込み」は，2次元流れを極座標にしていました。ですが，直交座標を極座標へ変換しているだけですから，極座標も同様に直交座標へ変換できれば，今まで扱ってきた2次元にグラフを描くことができます。
　前回の記事を読んでいいない方や「わき出しと吸込み」が分からないという方は，確認してみてください。

（２）わき出しの場合

（２-１）速度ポテンシャルと流れ関数

　では，式（１），式（２）にわき出しの速度ポテンシャル及び流れ関数をそれぞれ示します。

　ここで思い出していただきたいのは，直交座標と極座標の関係です。いわゆる単位円を考えることで，2次元流れの極座標を直交座標にかくことができます。登場するのは，原点から任意の点までの距離（半径r）とx軸とのなす角θの2つで，半径rとx軸とのなす角θは，式（３）のように表せます。

　つまり，半径ｒとx軸とのなす角θが分かれば，2次元流れの直交座標（x ,y）に描くことができます。よって，式（１），式（２）にある半径ｒとx軸とのなす角θが主役になる形に式変形すればよいので，式（４），式（５）のように表せます。

　これでグラフを描く準備は整いました。たったこれだけなのですが，意外とここまで解説している教科書はありません（筆者は，上記の解説をしている流体力学の書籍は1冊しか知りません…）。ちなみに，速度ポテンシャルφと流れ関数ψについては，一定値であることから適当な値を代入して問題ないのです。
　あとは，グラフを描くときのテクニックになります。続けてグラフの描画をしてみましょう。

（２-２）Excelによるグラフ描画

　では，式（４）と式（５）を使って「わき出しのグラフ」を描画しましょう。そのために，表を早速作っていきましょう。そこで，今回はこのような仮定のもとでグラフを描画していきます。

【仮定】わき出しの強さQ=4[cm^2/s]
　仮定は以上です。たったこれだけでグラフ描画できるのです。また，速度ポテンシャルφと流れ関数ψはそれぞれ－2.0～2.0まで0.2刻みで行います。

　それでは，表の作成を行います。Q，φ，ψをそれぞれ設定できたので，式（４）及び式（５）を使って計算を行います。注意としては，式（５）のθがラジアン表示になるので，わかりやすくするため，今回は度数法表示も併せてかいています（表１参照）。これを使って，その他の直線（等ポテンシャル線）と円（流線）を描くのに使っていきます。

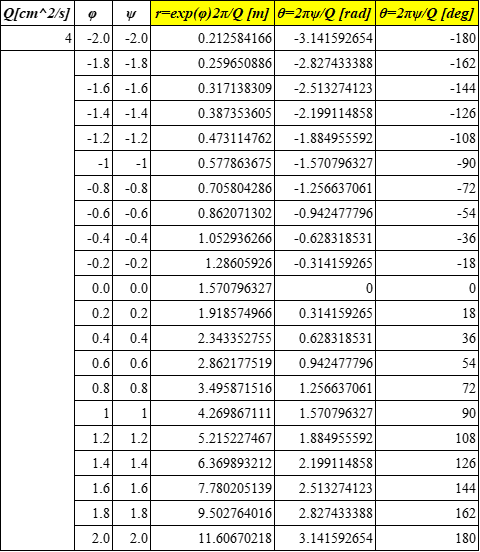
表１　わき出しの半径ｒとx軸とのなす角θの計算結果

（２-３）流線の描画

　では，次に直線，いわゆる流線の描画をしてみます。先ほどの表１のような表は正直，式変形ができれば誰でもできるのです。しかし，直線を描画するには少し頭を使う必要があります。考えるべきポイントは2点です。
　1点目は，直線の描画です。これについては，勘の良い人ならわかります。直線の描画には，中学2年に習う一次関数を考えると，傾きと切片が必要です。但し，原点を通過する場合なら傾きだけで問題ありません。では，傾きは何で表せるのでしょうか。単位円を使って考えると正解は，タンジェントθ（tanθ）です。つまり，式（５）で算出したx軸とのなす角θを使って，tanθを算出すれば「傾き」は表せます。
　2点目は，傾きに必要な変数の設定です。これは，筆者の考える一番のポイントです。1点目の傾きが算出はできても，変数xの設定が別途必要なのですが，これができずに多くの人はグラフ描画ができずに挫折してしまうことが多いように思います。
　それでは，変数xの設定をしていくのですが意外と簡単です（単純なものほど気づかないことが筆者もよくあります…）。

実は，変数xの設定は「自由」なのです。

　「えっ」と思われる方もいるかと思いますが，本当です！ もちろん，条件により変数の値の範囲が制限されることはあります。但し，今回取り上げる「わき出しや吸込み」の等ポテンシャル線について，変数の値の範囲は制限されません。よって，図１や図２を参考にすれば，流線（直線）はマイナスの範囲から原点を通過し，プラスの範囲に描画されます（数学的には，第３象限から第1象限，もしくは第２象限から第４象限に直線を描くことを意味します）。そのため，変数xはマイナスからプラスの値をとるように設定すればよいので，今回は，ｘ：―20～20（1刻み）で行いました（表２参照）。

表２　流線の計算結果

図３　流線の２次元流れ

　これで，流線（赤線）が描画できました（図３参照）。ここで注意なのが，表2の薄緑色（表の下部）については描画していません。なぜなら，表2の水色（表の上部）と同じ値になっていることが分かるからです。

（２-４）等ポテンシャル線の描画

　流線の描画の次に，等ポテンシャル線の描画を行います。表１の計算結果をもとに円を描くためにx, yを算出するために，式（３）を利用します。ここで決まっている値と変数の値を整理します。
　まず，決まっている値は半径rです。表１の計算結果から２１通りあることが分かるはずです。
　一方で，変数の値はx軸のなす角θです。そして，流線では，値の範囲に制限がありませんでしたが，x軸のなす角θには範囲の指定があります。その理由は，円を描くためです。要するに，円を描くには原点を中心に一周しなければならないので，θの範囲は，－π≦θ≦π（－180°≦θ≦180°）が必要になります。
　以上のことを踏まえ，表３に等ポテンシャル線の計算結果を示し，図４には，流線に加えて等ポテンシャル線の２次元流れをそれぞれ示します。

表３　等ポテンシャル線の計算結果

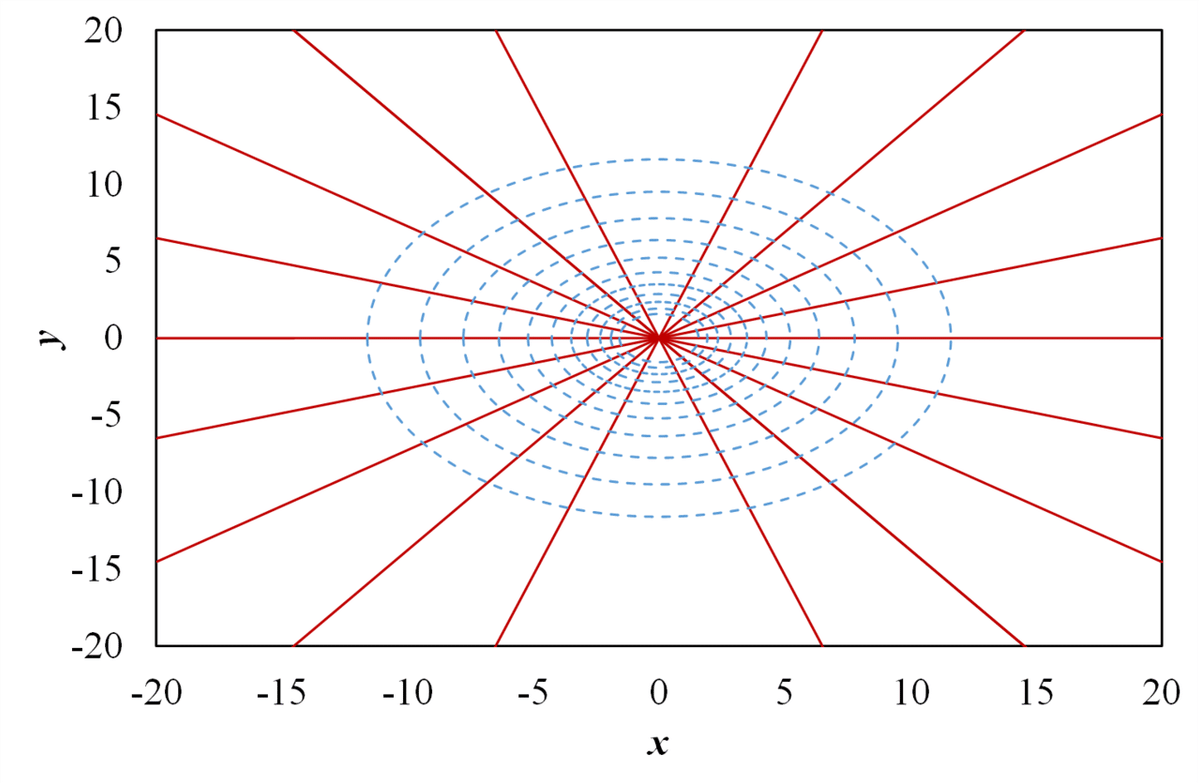
図４　等ポテンシャル線の２次元流れ

　これで，等ポテンシャル線（青点線）と流線が描画できました。ここで図４の注意としては，半径r=1.571以降を描画しています。理由としては，あまりに細かく描画しても，円がただの点に見えてしまうためです。本来は描画するべきなのですが，今回はあくまで見やすさを優先しました（そう思うのは，筆者だけかもしれませんが…）。

（２-５）等ポテンシャル線と流線の交点

　最後に，等ポテンシャル線と流線の描画を行った結果に，速度ポテンシャルと流れ関数の値が同値のときの交点を描画します。そのためには，表１の計算結果を使います。半径rとx軸とのなす角θが既に算出できているので，これを2次元の直交座標(x, y)に描くために式（３）を用いて，xとyをそれぞれ算出します。結果を表４に示し，図５及び図６には等ポテンシャル線と流線の交点を等ポテンシャル線と流線上に描画したものと交点のみをそれぞれ示します。

表４　わき出しの計算結果

図５　わき出しの2次元流れ（等ポテンシャル線と流線あり）

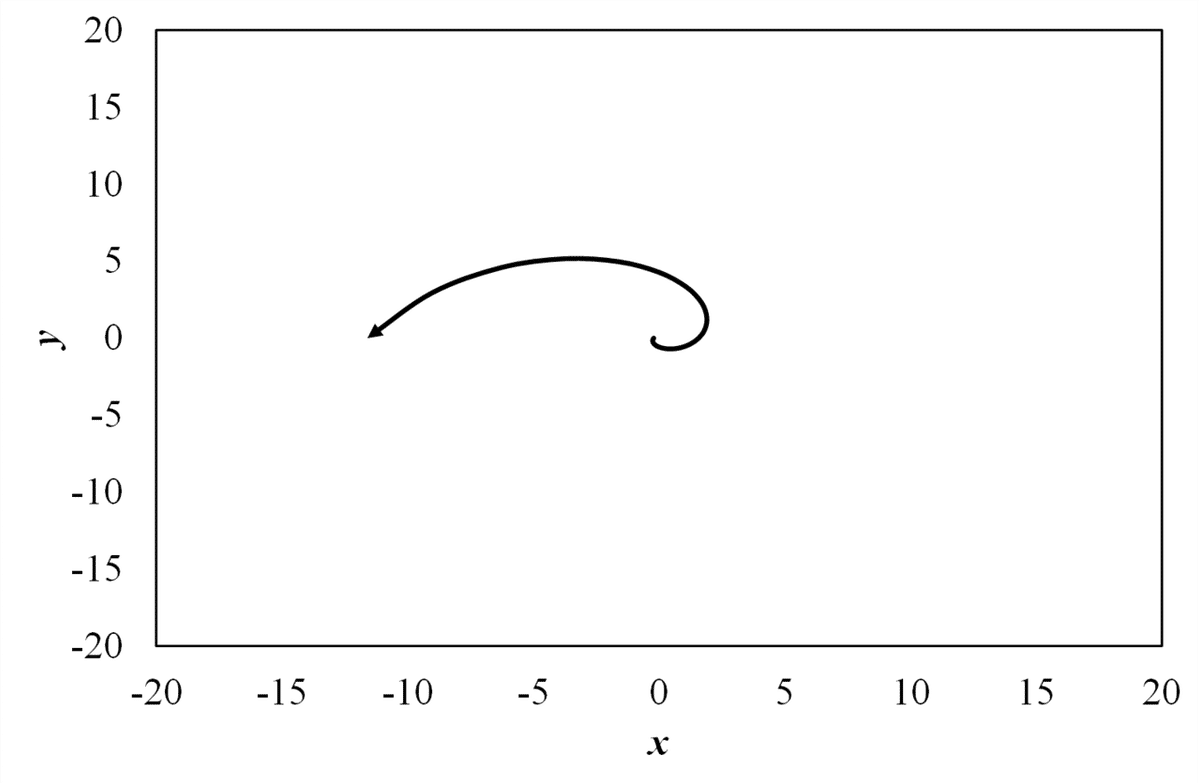
図６　わき出しの2次元流れ（等ポテンシャル線と流線なし）

　これで「わき出しのグラフ（プロット付き及びプロットなし黒線）」が描けました。しかし，勘の良い方なら，「表１からさっさと計算して表４からグラフを描けばよいのでは？」と思われるでしょう。それではダメなのです。
　その最大の理由は，わき出しと吸込みのグラフを描くためには，「等ポテンシャル線と流線の交点」をつないだものであることを知っている必要があるからです。これは，教科書には載っていないことが多いのです。だからこそ，最初のうちは時間をかけても知っておく必要があると筆者は考えております。

（３）吸込みの場合

（３-１）わき出しとの違いは？

　先ほど，「わき出しのグラフ」を描きましたが，今度は「吸込みのグラフ」に挑戦します。ここで，また一から表を作り直すのはまだ早いです。見るべきは，わき出しと吸込みの速度ポテンシャルと流れ関数の式なのです。式（６）と式（７）に吸込みの速度ポテンシャルと流れ関数をそれぞれ示します（参考として，わき出しの式（４）と式（５）も併せて，以下に記載します）。

　両者を比較すると，わき出しと吸込みの違いは速度ポテンシャルにマイナスが付いただけです。つまり，わき出しの計算結果である表１との違いは，半径rを求めるときにマイナスをつけるだけでいいのです。
　よって，吸込みの計算結果を表５（橙色が変更箇所）に示し，図７及び図８には等ポテンシャル線と流線の交点を等ポテンシャル線と流線上に描画したものと交点のみをそれぞれ示します。

表５　吸込みの半径ｒとx軸とのなす角θの計算結果

図７　吸込みの2次元流れ（等ポテンシャル線と流線あり）

図８　吸込みの2次元流れ（等ポテンシャル線と流線なし）

　これが「吸込みのグラフ」です。この結果から，わき出しと吸込みの結果が何となくわかったと思います。そして，これが「わき出しと吸込み」の片方が省略される理由でもあります。グラフの形があまり変わらないうえに，わき出しと吸込みの式も速度ポテンシャルしか変わらないからです。

　更に言えば，大学・高専がなぜグラフまでの議論に踏み込まないのかの理由も…。
　但し，ここにかく内容はあくまでも筆者の個人的主観に基づいたものであることを予め断っておきます。その最大の理由は「時間がない」からです。一年という僅かな期間で，流体力学の座学をシラバス通りに基本的には進行しなければならないので，まず，座学ではグラフを描かせずに式とグラフの形だけを教えます。
　その後，機械工学実験などの時間で，学んだ内容を補うために例えば「円柱回りの流れに関する実験」を実施し，流れの様子を描画させるなどが定番だと思います。
　しかし，すべての大学に当てはまるとは思いませんが，近年の学科統合で機械工学（特に４力学）に多くの時間をかけることができなくなっています。このことを知っている大学・高専の先生方は構いませんが，学生が学ぶという観点からは本当に技術者として生きていくことを考えると「どうかな？」と筆者は思っています。皆様はどうお考えでしょうか？

　以上でグラフの解説は終わります。

（４）まとめ

　今回の記事のまとめを以下に示します。
（１）グラフを描くためには，わき出しと吸込みの速度ポテンシャルと流れ関数を半径rとx軸とのなす角θが主役になる形に式変形する必要がある。
（２）「わき出しと吸込み」のグラフは，「等ポテンシャル線と流線の交点」から描画することができる。
（３）わき出しと吸込みの違いは，速度ポテンシャルに「マイナス」が付くことのみある。

　以上です。最後まで閲覧頂きありがとうございました。

※次回は，渦の2次元流れについて扱う予定です。

（５）おまけ

　図９にわき出し・吸込みの2次元流れのグラフを示します。かなり前に描いたものなので，わき出しか吸込みかは忘れてしまいました（恐らく，吸込みと思われる）が，方眼紙に2次元流れを描いたものです。実は，グラフがExcel上で描けない場合の最終手段は「手書き」でグラフを描くことかもしれませんね（笑）。

図９　わき出し・吸込みの2次元流れ（方眼紙による描画）