流体力学　循環の証明

　皆様おはこんばんちは。そして，お疲れ様です。

　最近，流体力学を再度学び直してみようと思い，記事にしています。
　第３２回目は，第３１回目の予告通り「循環の証明」について紹介していきます。

（１）循環の復習

　 以前に「循環」について，解説を行いましたが，実はサラっと式変形を通過したものがあります。その式を以下に示します。参考は，以前の記事を参考にしてみて下さい。

　式（１）にストークスの定理を用いると，式（２）のように表せます。

　式（２）の下線部が以前に解説した渦度ζに該当する部分です。これが，サラっと通過した箇所です。

　式（１）から式（２）に式変形する際に「ストークスの定理」を用いる訳ですが，多くの教科書でも証明が省かれる，もしくは付録にて証明されるもので解説されること自体が少ないものです。
　解説が少ない理由としては，流体力学に触れる前段階で「応用数学（解析学など）」の名称で「ベクトル解析」という分野で必ず触れることや証明するために割く時間がない等が考えられますが，基本的にはあまり重要視されていないためと筆者個人は考えています。
　筆者は，このようなよくわからない定理を利用して証明する等の記述を見ると，重要ではなくとも必ず知りたくなります。そのようなもの好きな方がどのくらいいるのかは不明ですが，このストークスの定理，厳密には「平面のグリーンの定理」について解説してみます。

（２）平面のグリーンの定理

　では，平面のグリーンの定理を証明してみましょう。まず，図1に示すように，2つの実関数P(x, y)とQ(x, y)がxy平面上に閉曲線Cで囲まれた線上および内部で連続な偏導関数を持つときは，以下のような式（３）が成立します。但し，閉曲線Cは左回転（時計の針と反対方向）が正回転とします。この正方向に沿って積分を行います。

図1　平面のグリーンの定理の閉曲線C

　ここで，図1に示していますが，y軸に平行な２つの接線x=a（点A），x=b（点B）と任意のy軸に平行な直線と閉曲線の交点C1，C2とします。
　
　次に，以上のように示した積分経路を利用して実関数P(x, y)を証明します。積分経路に気を付けながら式変形を行うと，式（４）のように表せます。

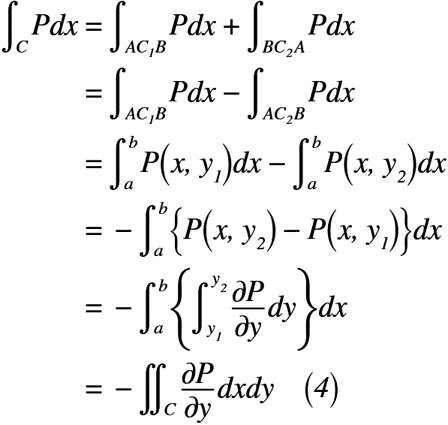
　同様に，実関数Q(x, y)も証明すると，式（５）のように表せます。

　よって，式（４）と式（５）を加えると，式（３）のように表せます。
　これがストークスの定理，厳密には「平面のグリーンの定理」が証明出来ました。したがって，当初の証明に必要な式（１）から式（２）の証明もできることが分かりました。
　では，なぜストークスの定理と説明したかというと，「グリーンの定理」はストークスの定理の特殊な場合に成立したものを示すからです。厳密にいえば，ストークスの定理のベクトル場f = [f, g, h]の形からf = [f, g, 0]の場合の形を示したものになります。

（３）まとめ

　今回の記事のまとめを以下に示します。
（１）循環に必要なストークスの定理，厳密には平面のグリーンの定理の証明が必要になる。
（２）グリーンの定理は，2つのx, y平面上に閉曲線Cに囲まれた領域で成立する。
（３）グリーンの定理は，ストークスの定理のベクトル場f = [f, g, 0]と置いた特殊な場合である。

　以上です。最後まで閲覧頂きありがとうございました。

※次回は，「渦に関する法則」について取り上げる予定です。

　※「任意の角度を回る流れのグラフ」については，別日に投稿しますので，少々お待ちください。言い始めてから１ヶ月以上経過していることは内緒です。汗