
補足編 対数関数の微分
皆様おはこんばんちは。
最近,流体力学を再度学び直してみようと思い,記事にしています。
今回の補足編は,第54回目の「シュワルツ・クリストッフェルの定理(その3)」で使用する対数関数の微分について取りあげます。記事で使う予定の問題は,最後に取り上げます。この問題は,筆者にとって苦い思い出のある問題です。最後に「おまけ」として紹介します。
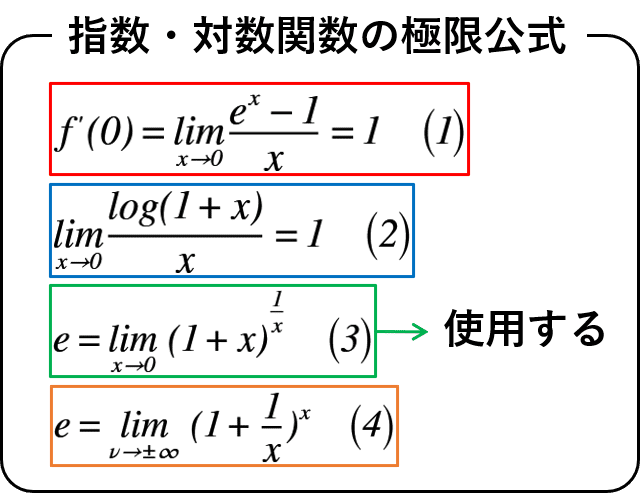
(1)指数・対数関数の極限公式
さて今回は,対数関数の微分を取り上げますが,そのための準備として指数・対数関数の極限公式から掘り下げてみましょう。
ここで,微分係数の定義式から取り上げていきます。

全ては微分係数の定義式に示す通りx・yの増加量と極限の関係から始まります。図1に指数関数y=f(x)=a^x (a>1)のx=0における微分係数f’(0)は,以下のようになります。


図1に示すように,このf’(0)が1となるときの底aの値を「ネイピア数e」として定義できると,以下のようになります。

上式の文字定数hをxに置換すると,式(1)のようになります。

ここで,e^x-1=uに置換すると,以下のように式変形ができます。

また,極限も考えましょう。変数がとある値のとき,他の定数がいくつになるかを考えればよいのです。今回はx→0のとき,u→0となるため,式(1)に置換式と極限を代入すると,以下のようになります。

上式の点線部のみをまとめると,以下のようになります。

上式の文字定数uをxに置換すると,式(2)のようになります。

では,式(2)を変形すると,以下のようになります。

上式の点線部のみをまとめると,式(3)のようになります。

式(3)に対して,1/x = νと置換し,極限もx→0のとき,ν→±∞となることを使うと,以下のようになります。

上式の文字定数νをxに置換すると,式(4)のようになります。

以上より,指数・対数関数の極限公式が全て導入できました。但し,これらの公式のなかで今回の記事で使用するのは,残念ながら式(3)のみです。図2に,指数・対数関数の極限公式をまとめておきます。
(2)対数関数の微分公式1
次に,対数関数の微分公式を導出します。式(5)は,対数関数の微分の結果であり,理系の方なら見慣れた式だと思いますが,いざ導出となると困るものです。

では,導出するあたって微分係数の定義式を使用します。特に,対数の性質を使うことと文字定数1/x,x/hに分けて考えることがポイントです。これらの考え方を使うと,以下のようになります。

ここで,k=h/xと置換することと,極限を考えます。今回はh→0のとき,k→0となることを使用し,対数の性質と式(3)を代入すると,式(5)が得られます。

以上で式(5)の証明は完了です。前項の式(3)を忘れると,微分係数の定義式や対数の性質を知っていても導出できないのです。
(3)合成関数の微分公式
次に,合成関数の微分公式を導出します。y=f(t),t=g(x)がともに微分可能なとき,合成関数y=f(g(x))も微分可能で式(6)が成立します。式(6)は,理系の方なら見慣れた式だと思いますが,これもいざ導出となると困るものです。

では,y=f(t),t=g(x)を合成した関数であるy=f(g(x))を微分係数の定義式に当てはめると,式(7)のようになります。
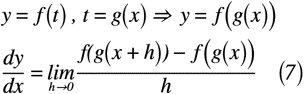
合成関数y=f(g(x))をxで微分すると,以下のようになります。気を付けるべきポイントは,図3のように後ろ引く前の関係になっているu=g(x+h)-g(x)に注意することでしょうか。


上式の結果から,極限はh→0のとき,u→0となります。この極限とg(x)=tと置換した単項式を式(7)に代入すると,以下のようになります。

極限(h→0のとき,u→0)とx・yの増加量を考慮した微分係数の考え方を用いると,f(t)とg(x)の微分となるため,結果的に合成関数の微分公式(6)となります。

(4)対数関数の微分公式2
次に,対数関数の微分公式2を導出します。式(8)は,対数関数の微分の結果であり,式(5)の単項式から多項式に変えただけのものです。この式(8)は前項の合成関数の微分公式を使って導出してみます。

まず,与式はy=logf(x),f(x)=tの2つを考えて,y=logf(x)をxについて微分します。このとき,合成関数の微分公式(6)を使って出すと,以下のようになります。

与式をそれぞれt,xについて微分した結果を使うと,対数関数の微分公式(8)が得られます。

式(8)は,式(5)の単項式から多項式に変えただけのものですが,意外と合成関数の微分を知らないと証明できないのです。
(5)対数関数の微分問題
お待たせしました。これが本題として取り上げたかった対数関数の微分問題です。求めたい与式は,式(9)です。

これをxについて微分することで得られる結果を求めていきます。ポイントは,対数関数の微分公式(8)を利用すると,単項式ごとに微分ができるため,以下のようになって式(10)が得られます。

式(10)の結果は,「シュワルツ・クリストッフェルの定理(その3)」で取り上げる問題で利用します。
(6)まとめ
今回の記事のまとめを以下に示します。
① 指数・対数関数の極限公式は,4つにまとめられる。
② 合成関数の微分公式は,2つの関数が微分可能で極限も0に収束することが前提である。
③ 対数関数の微分公式は,単項式でも多項式でも同様の公式形態となる。
以上です。最後まで閲覧頂きありがとうございました。
(7)おまけ
最後に,筆者にとって苦い思い出をお話ししましょう。
(5)の対数関数の微分問題は,高専3年生の数学で実際に出題された問題でした。結論か言えば,試験当日は解けませんでした。問題文は,「与式を微分しなさい」ではなく,「与式を証明しなさい」と書いてありました。
たった2文字しか違いませんが,試験当日に「???」となり,問題が解けなかったという苦い思い出でした。当時の数学の試験は他で挽回ができたため,赤点ではありませんでした。
しかし,未だに微分積分の苦手意識が抜けないきっかけとなった筆者の懺悔でした。
いいなと思ったら応援しよう!

