流体力学　循環

　皆様おはこんばんちは。そして，お疲れ様です。

　最近，流体力学を再度学び直してみようと思い，記事にしています。
　第３１回目は，前回の予告通り「渦度」について紹介していきます。

（１）循環とは？

　 では，「循環」について解説してみます。以前の記事でも「渦流れ」について取り上げましたが，その違いも含めて書いていきます。
　結論から言えば，「両者はほとんど同じこと」を言っています。例えば，以前解説した渦流れなしの場合，循環もゼロとなります。
　つまり，渦の数学的表現であることは変わりません。ほとんど変わらないように見える両者ですが，筆者個人的の考えとしては，図1のように考えています。

図1　渦流れと循環のイメージ

　なぜこのようなイメージなのかというと，「渦」が目に見えるか見えないの判別ができるためです。「渦流れ」は，今までの解説してきたものが全て「渦が目に見える状態」のものを扱ってきました。その一方で，「循環」は，渦の考えるときの物理量で流体に「渦が目に見える状況ではない」ものも取り扱えるようになります。
　よって，循環の方が渦流れよりも前に来る理論だと考えています。

（２）循環の式

　では，循環の式を考えるために，必要な条件を整えていきます。2次元流れの上に１つの閉曲線Cを描きます。そのイメージを図2に示します。ちなみに閉曲線Cは以前に「渦度」で解説した通り，「渦管の断面」を示しています。

図2　循環のモデル

　この閉曲線C上に流速q，閉曲線の微小長さ（線素）ds，流速qと閉曲線の微小長さdsのなす角θとします。循環Γ（ガンマ）は，「速度qの線素ds方向成分であるqcosθdsを閉曲線に沿って反時計回りに1周積分した値」となります。
　よって，循環Γは式（1）のように表せます。

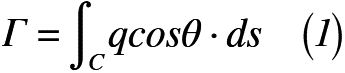
　流速qのx, y方向速度u, vとおくと，流速qと線素dsの方向余弦をそれぞれ考えます。言葉は難しいですが，結局のところ直角三角形を考えればよいだけなので，図3から式（2）のように表せます。

図3　流速qと線素dsの方向余弦の考え方

　ここで，式（２）を式（１）へ代入すると，式（3）ののように表せます。

　式（３）にストークスの定理を用いると，式（４）のように表せます。ストークスの定理については，後日記事にする予定です。

　式（4）の下線部が以前に解説した渦度ζに該当する部分です。つまり，渦管を取巻く閉曲線に沿っての循環は渦度の面積積分に等しいことが分かるため，循環Γと渦度ζの関係が成立します。
　よって，図1で説明した渦流れと循環のイメージのような関係ができると筆者は考えています。

（３）まとめ

　今回の記事のまとめを以下に示します。
（１）循環と渦流れには関係性が存在する。
（２）循環のモデル化には，閉曲線Cを渦管の断面に見た立てたうえで行う。
（３）循環には，方向余弦とストークスの定理が証明には必須である。

　以上です。最後まで閲覧頂きありがとうございました。

※次回は，ストークスの定理，循環の証明の2つについて扱う予定です。時間的に間に合えば，２つの記事を同時投稿する予定とします。

　※「任意の角度を回る流れのグラフ」については，別日に投稿しますので，少々お待ちください。言い始めてから１ヶ月以上経過していることは内緒です。汗