
流体力学 2重わき出しのグラフ
皆様おはこんばんちは。そして,お疲れ様です。
最近,流体力学を再度学び直してみようと思い,記事にしています。
第22回目は,第21回目で予告した通り,「2重わき出しのグラフ」について紹介していきます。
(1)円の方程式を再度確認すると…
では,2重わき出しのグラフを描くために以前の記事で紹介した円の方程式を確認しましょう。式(1)に2重わき出しの流れ関数ψから円の方程式を導出した結果を示します。
もし,以前の2重わき出しの複素関数が分からない方は,以下の記事を参考にしてみて下さい。
また,式(2)には以前に記事で紹介し忘れた2重わき出しの速度ポテンシャルφから円の方程式を導出した結果を示します。


では,式(1)と式(2)を使って,2重わき出しのグラフを描いていきましょう。以前のわき出しと吸込みのグラフとは異なることがあるのですが,それは次項で取り上げましょう。
(2)グラフ準備(概略図から分かること)
以前の記事でも掲示していた2重わき出しの概略図を図1に示します。

図1 2重わき出しの概略図
ここで,わき出しと吸込みの合成から2重わき出しに変える条件としては,「座標の一定値εを限りなく原点0に近づけること」です。そのため,速度ポテンシャルと流れ関数から得られる円の端部が「必ず原点を通過する」ことなのです。なので,式(1)と式(2)を使えば,2重わき出しのグラフが描けるのです。
但し,ここで注意しなければいけないのが,式(1)と式(2)にそのまま代入しても円が同心円状に描けるだけなのです,そのため,同心を偏心にするためには,半径の長さ分だけずらすことを行います。図2に,同心円状から偏心円状の変換イメージを示します。

図2 同心円状から偏心円状の変換
この変換を上手く使うことで,式(1)と式(2)を使って,2重わき出しのグラフをきちんと描くことが出来ます。
(3)2重わき出しのグラフを描くためには…
ここまでの解説を使って,2重わき出しのグラフを描きましょう。それでは,今回のグラフ描画に必要な仮定を以下にそれぞれ示します。
【仮定】2重わき出しの強さm=15cm/s,速度ポテンシャルφ=±5,流れ関数ψ=±5(但し,いずれもゼロは除く。)
それでは,以前の記事で分かる通り,半径r=m/2ψ,r= m/2φになることを考慮すると,計算結果は表1のように表せます。
表1 半径の計算結果

この結果を用いることで,極座標の関係式を使うことが出来ます。式(3)に極座標の関係式を示します。この式を使うことで円のグラフを描くことが出来ます。表2に流れ関数の計算結果,表3に速度ポテンシャルの計算結果をそれぞれ示します。
![]()
表2 流れ関数の計算結果

表3 速度ポテンシャルの計算結果

よって,これらの結果を用いて2重わき出しのグラフを描画できます。図3に流れ関数の2重わき出し,図4に速度ポテンシャルの2重わき出し,図5に2重わき出しの合成のグラフをそれぞれ示します。

図3 流れ関数の2重わき出し
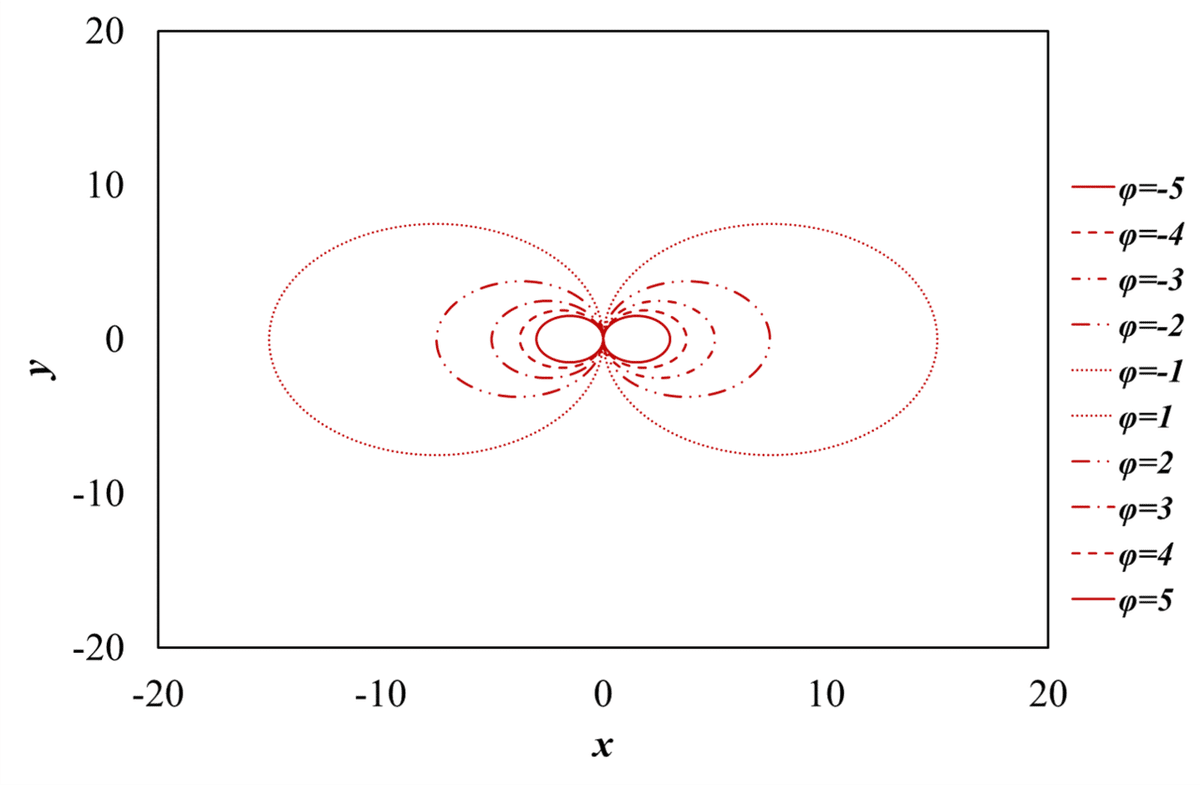
図4 速度ポテンシャルの2重わき出し
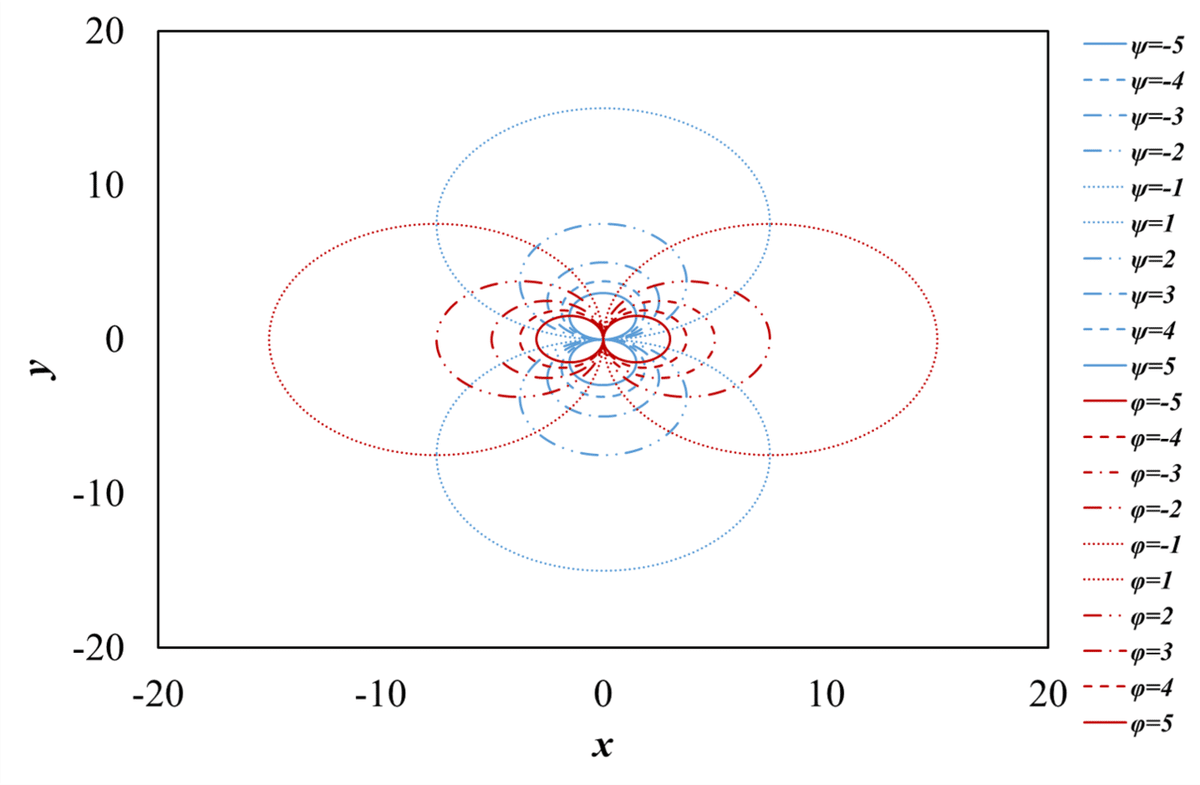
図5 2重わき出しの合成のグラフ
これより,式(1)と式(2)及び偏心円状への変換を行うことで2重わき出しのグラフを描画できました。
(4)まとめ
今回の記事のまとめを以下に示します。
(1)2重わき出しの速度ポテンシャルと流れ関数から円の方程式が導出できる。
(2)2重わき出しのグラフに適用するためには,半径の長さ分だけ偏心させることが必要になる。
以上です。最後まで閲覧頂きありがとうございました。
※次回は,一様流れと2重わき出しの合成について扱う予定です。
(5)おまけ
2次元流れに興味のある方々は,2重わき出しのグラフは簡単に思われたのではないのでしょうか。筆者もその一人です。しかし,実際には座標の一定値εがゼロになることで式を簡単にできるとともに,グラフも描画しやすくなるのです。
これが,近似式である「マクローリン展開」の威力だと筆者は思っています。恐らく,数学・物理学を厳密に議論する方からすれば,このような近似は「邪道」なのかもしれませんが…。
しかし,その業界でも数十年,数百年後の証明で「その近似は正しいのです!」と言われても「だから何?」になってしまうのですが,筆者の個人的な意見としては非常に興味深い証明です。
サポートをして頂けると大変助かります。何かの支援ができるかもと思われた人をは何卒よろしくお願いします!
