流体力学　一様流れのグラフ

　皆様おはこんばんちは。そして，お疲れ様です。

　最近，流体力学を再度学び直してみようと思い，記事にしています。
　第１１回目は，第１０回目でネタにした「一様流れ」を使って「流れの様子」をかくための「グラフ」について紹介していきます。

（１）一様流れとは

　さて，一様流れを含め，多くの流体の様子を記述するには，ポテンシャル流れと流れ関数を含む複素関数とコーシー・リーマンの微分方程式が必須となります。詳しくは，前回の記事を確認してみてください。

　今回のテーマはなぜ「グラフ」なのでしょうか？

　私が，この分野を独学しているときに非常に疑問にだったのは，「なぜグラフを書かないのだろう？」，「なぜグラフに言及したものがないのだろう？」と思ったことです。
　もちろん，大学・高専の定期試験，技術士一次試験や技術系公務員試験等でもグラフを書かせることはないので，結局のところ与式を見たときに，流れのグラフがイメージできていれば，試験に受かるためだけを考えれば，問題ないわけです。
　しかし，「グラフを書けないとレポートとして報告できない」，「実感することなくただ暗記するだけになりかねない」という観点から，やっぱりグラフを書けることに損はないと筆者は考えています。

　流体力学の学び直しで多くの書籍を参考にしていますが，このグラフに言及している書籍は，筆者は一冊しか知りません（誰か他に言及しているものを知っている人は教えてほしい…）。
　これが今回「グラフ」をメインに扱う理由です。今回のグラフ描画には，皆さん大好きExcelで行っています。

（２）一様流れ（x軸方向流れ）

　では，前回の記事と同様に，以下の例題を考えてみましょう。

【例題１】u= U，v=0　u, v：2次元流れのx, y方向の速度

　グラフに描画するのに使うのは，速度ポテンシャルφと流れ関数ψなので，式（１）にそれぞれ示します。

　多くの教科書では，ここで一様流れのグラフが表示されて終了です（前回の記事でもあえてそのようにかきました）。
　では，グラフにするには，式（１）を式（２）に書き直しておく必要があります。

　数式の準備はこれだけです。また，グラフを書く前に気づくべき点は2点です。
　1点目は，2次元流れのx, y方向の速度U, Vは，実験等で算出できる数値であることです。つまり，問題になれば与えられる値，実験であれば調べて分かる値であることなので，何も考える必要がないのです。
　2点目は，速度ポテンシャルφと流れ関数ψは，一定値（constant number = const.）であることです。言い換えると，「適当に値を勝手に決めていいいということ」です！
　この2点さえ分かっていれば，グラフを書くための準備は完了です。

　ここで，U=5.0[m/s]，φ及びψを1.0刻み（1.0～5.0）にしてグラフを描画します。グラフ作成に使用した表１と図１をそれぞれ示します。

表１　一様流れ（x軸方向流れ）使用した数値一覧

図１　x軸方向流れ

　いかかでしょうか。グラフを実際に書くためにはたったこれだけで十分なのです。
　少し難しい箇所があるとすれば，今回はx及びyの値がx, yの値の変化に関係なく，常に一定値となるので，値を固定している箇所があることでしょうか（表１の灰色箇所を参照すること）。

（３）一様流れ（ｙ軸方向流れ）

　では，前回の記事と同様に，以下の例題を考えてみましょう。

【例題２】u=0，v=V　u, v：2次元流れのx, y方向の速度

　グラフに描画するのに使うのは，速度ポテンシャルφと流れ関数ψなので，式（３）にそれぞれ示します。

　多くの教科書では，ここで一様流れのグラフが表示されて終了です（前回の記事でもあえてそのようにかきました）。
　では，グラフにするには，式（３）を式（４）に書き直しておく必要があります。

　数式の準備はこれだけです。次にグラフをかきましょう。ここで，V=5.0[m/s]，φ及びψを1.0刻み（1.0～5,0）にしてグラフを描画します。グラフ作成に使用した表２と図２をそれぞれ示します。

表2　一様流れ（x軸方向流れ）使用した数値一覧

図２　y軸方向流れ

　前回の記事で，「ただ線をつなぎ合わせただけだな…」と思っていただいた方がいたら，嬉しいです。なぜなら，今回グラフを書くためにわざとそのようにしたのですから。
　ちなみに，図１と図2の流量Qは速度ポテンシャルφと流れ関数ψの差で求まります。但し，奥手方向（スパン方向）は長さ１として考えるので，単位としては[m^2/s]となります。

（４）一様流れ（x, y軸方向流れ）

　　では，前回の記事と同様に，以下の例題を考えてみましょう。

【例題３】u=U，v=V　u, v：2次元流れのx, y方向の速度

　　グラフに描画するのに使うのは，速度ポテンシャルφと流れ関数ψなので，式（５）にそれぞれ示します。

　多くの教科書では，ここで一様流れのグラフが表示されて終了です（前回の記事でもあえてそのようにかきました）。
では，グラフにするには，式（５）を式（６）に書き直しておく必要があります。

　数式の準備はこれだけです。次にグラフをかきましょう。ここで，U=5.0[m/s]，V=5.0[m/s]，φ及びψを1.0刻み（-5.0～5,0）にしてグラフを描画します。グラフ作成に使用した表3と図3をそれぞれ示します。

表3　一様流れ（x, y軸方向流れ）使用した数値一覧

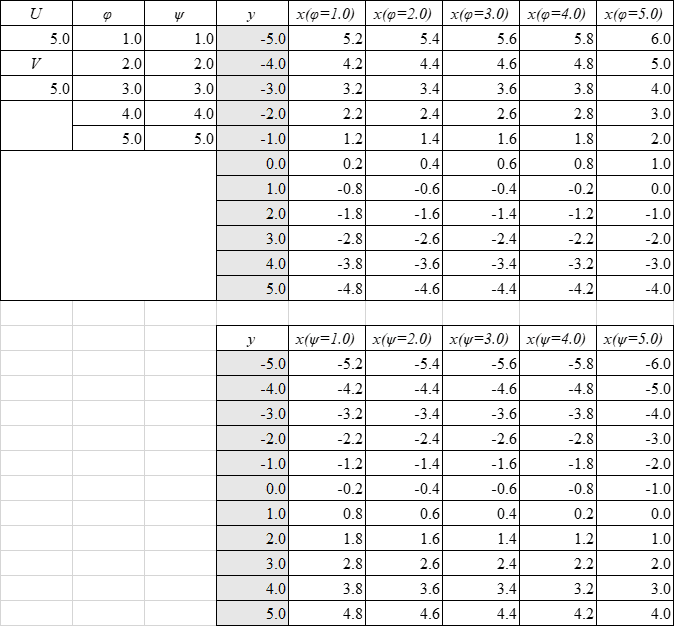
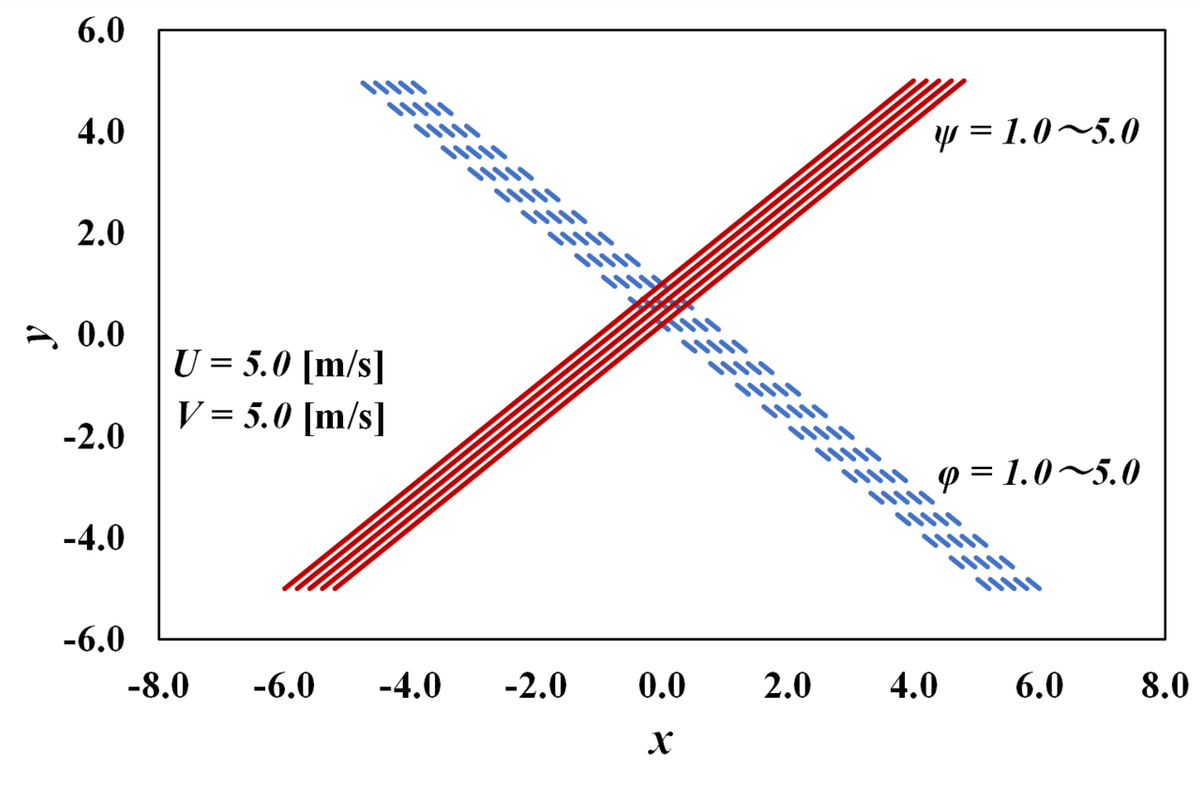
図３　ｘ, y軸方向流れ

　間隔が詰まって少しわかりづらいですが，教科書に使っている図がいかに「見せるため」の図であることも分かっていただけると思います。

（５）まとめ

　今回の記事のまとめを以下に示します。
（１）一様流れの2次元流れのx, y方向の速度U, Vは，一定値のため，設問で与えられるまたは実験で測定できる。
（２）コーシー・リーマンの微分方程式から得られた速度ポテンシャルφと流れ関数ψからグラフをかくためには，式変形する必要がある。
（３）グラフをかくためには，速度成分U, V以外に，速度ポテンシャルφと流れ関数ψの刻み幅を一定に適当な値を設定する必要がある。

　以上です。最後まで閲覧頂きありがとうございました。

※次回は，吸い込み・湧き出しを扱う予定です。