
生存時間分析の基礎 6(比例ハザード仮定の検討 その 2)
生存時間分析の基礎の第 6 回目となります.
今回もぼちぼちやっていきましょう.
前回は Cox PH モデルの前提である「比例ハザード仮定」が成立しているかどうかを検証する方法として,グラフを使う方法を解説しました.
グラフを使う方法はグラフを視て判断するという定性的な方法でした.
どんな方法であったか忘れてしまった方は前回を振り返ってみてください.
今回からは,都合数回に渡って定量的な統計的検定手法である「適合度を使った方法」をみていきたいと思います.
分析結果を公にリリースするような場合(例えば,研究論文など)では,検定を利用した定量的な方法が広く使われていると思います.
比例ハザード仮定を検証するための統計的検定手法はいくつか提案されていますが,この記事では最も代表的な手法である Schoenfeld 残差 を使った Harrel and Lee の検定をみていきたいと思います.
一気に説明しようとすると長くなってしまいますので,今回は Schoenfeld 残差に関して詳しく見ていくことにし,検定に関しては次回に回します.
1. Shoenfeld 残差
残差とは「モデルによる推定値と観測値の差」のことですが,この残差を分析することでモデルの当てはまり具合などの妥当性を検証することができます.
例えば,線形モデルにおける決定係数はモデルの当てはまり具合を表す指標ですが,実は推定値と観測値の差である残差と密接に関係しています.
(どのように関係しているかご存知ない方は Wiki を見てみてください)
線形モデルにおける残差は,各データ(対象)毎に推定値と観測値の差を計算すれば良いだけです.しかし,生存時間分析では打ち切り対象などを含むため,線形モデルのように単純ではなく生存時間分析に適した残差を使用することになります.
生存時間分析の残差には,
Martingale 残差
Shoenfeld 残差
Score 残差
Deviance 残差
などがあります.
残差分析としてよく使用されるのは Martingale 残差や Deviance 残差のようですが,今回は冒頭でお話したように Shoenfeld 残差に焦点をあててみていきましょう.ちなみに,Shoenfeld 残差はその名の通り David Shoenfeld 氏によって以下の論文で提案された残差となります.
手始めに第 4 回で解説した Cox 尤度を復習し,それから Shoenfeld 残差を理解していくことにします.
まず,ある対象 $${i \in D}$$($${D}$$ :イベントが発生した全集団)にある時間 $${t_{i}}$$ でイベントが発生した場合を考えます.その時点で生存している集団(リスクセット)は $${R_{i}}$$ とします.また, $${\bm{X}_{i} = (X_{i1}, \dots, X_{i \xi}, \dots, X_{ip})^T}$$ を $${p}$$ 個の 共変量をもつ対象 $${i}$$ の共変量ベクトル,$${\bm{\beta} = (\beta_{1}, \dots, \beta_{\xi}, \dots, \beta_{p})^T}$$ を推定すべき $${p}$$ 個の要素をもつ Cox PH モデルの係数ベクトルとします.
上記の状態が発生する確率 $${p_{i}}$$ は,第 4 回で具体例を示して確認した通り,ハザード関数の時間に依存する項が分子と分母間で打ち消しあった結果,下のように書くことができます(下式がよく分からない方は第 4 回の記事を復習することをお勧めします).
$$
\begin{array}{}
p_{i} &=& \frac{\exp(\bm{X}_{i}^{T} \bm{\beta})}{\sum_{k \in R_{i}} \exp(\bm{X}_{k}^{T} \bm{\beta})}
\end{array}
$$
そして,Cox 尤度 $${L}$$ はイベントが発生した全集団 $${D}$$ に対して上記の確率を全てかけ合わせたものになります.
$$
\begin{array}{}
L &=& \prod_{i \in D} \frac{\exp(\bm{X}_{i}^{T} \bm{\beta})}{\sum_{k \in R_{i}} \exp(\bm{X}_{k}^{T} \bm{\beta})}
\end{array}
$$
この Cox 尤度 $${L}$$ を最大化することで $${\bm{\beta}}$$ を求めるわけですが,便利のため対数尤度 $${LL}$$ の形にしておきましょう.
$$
\begin{array}{}
LL &=& \log \biggl( \prod_{i \in D} \frac{\exp(\bm{X}_{i}^{T} \bm{\beta})}{\sum_{k \in R_{i}} \exp(\bm{X}_{k}^{T} \bm{\beta})} \biggl) \\
\\
&=& \sum_{i \in D} \Biggl[ \bm{X}_{i}^{T} \bm{\beta} - \log \biggl( \sum_{k \in R_{i}} \exp(\bm{X}_{k}^{T} \bm{\beta}) \biggr) \Biggl]
\end{array}
$$
この対数尤度 $${LL}$$ をもとに,最尤法で係数を求めることになります.
対数尤度を $${\bm{\beta}}$$ の任意の要素 $${\beta_{\xi}}$$ で微分してあげると・・・
$$
\begin{array}{}
\frac{\partial LL}{\partial \beta_{\xi}} &=& \sum_{i \in D} \bigl( X_{i \xi} - A_{i \xi}(\bm{\beta}) \bigr) \\
\\
A_{i \xi}(\bm{\beta}) &=& \frac{\sum_{k \in R_{i}} X_{k \xi} \exp(\bm{X}_{k}^{T} \bm{\beta})}{\sum_{k \in R_{i}} \exp(\bm{X}_{k}^{T} \bm{\beta})}
\end{array}
$$
少しややこしいですが,上のようになります.
よって,ここまでの計算の結果,Cox 尤度を使った最尤法における $${\bm{\beta}}$$ の各要素 $${\beta_{\xi}}$$ の満たすべき式は
$$
\sum_{i \in D} \bigl( X_{i \xi} - A_{i \xi}(\bm{\beta}) \bigr) = 0
$$
ということになりました.
さて・・・実は,Shoenfeld 残差というものは上式の和記号の中の
$${X_{i \xi} - A_{i \xi}(\bm{\beta})}$$
のことを指します(ちなみに,Shoenfeld 残差を計算する際に使用する $${\bm{\beta}}$$ は最尤法で求めたものを使用します).
いきなりそんなこと言われても・・・と思われる方も多いと思いますので,この式の意味を直感的に考えてみます.
まず $${A_{i \xi}(\bm{\beta})}$$ は何を表しているかを考えてみましょう.
これは
「ある対象 $${i \in D}$$ が時間 $${t_{i}}$$ でイベントを起こした時,その時点での生存集団(リスクセット $${R_{i}}$$)における共変量 $${X_{ \xi}}$$ の期待値」
を表しています.
時間 $${t_{i}}$$ で実際にイベントを起こしたのは対象 $${i}$$ でしたが,仮にリスクセットに含まれる各対象がイベントを起こす場合,その発生確率は
$${\frac{\exp(\bm{X}_{k}^{T} \bm{\beta})}{\sum_{k \in R_{i}} \exp(\bm{X}_{k}^{T} \bm{\beta})}}$$
となります(これがどうしてか分からない方は Cox 比例ハザードの記事を復習しましょう.)
よって,$${A_{i \xi}(\bm{\beta})}$$ はリスクセットにおける $${X_{\xi}}$$ の期待値となっているわけです.$${A_{i \xi}(\bm{\beta})}$$ が何を意味しているのかなんとなく分かりました.そして上の内容を踏まえれば,Shoenfeld 残差は「ある対象 $${i}$$ の共変量 $${X_{i \xi}}$$ とその対象 $${i}$$ にイベントが発生した時点でのリスクセットにおける共変量 $${X_{\xi}}$$ の期待値の差」になります.
ここで,もう一度 Cox PH モデルの前提である比例ハザード仮定を思い出してみましょう.Cox PH モデルにおけるハザード関数 $${h(t, X)}$$ は
$${h(t, X) = h_0(t) \cdot \exp({\sum^{p}_{i=1} \beta_i X_i})}$$
と表すことができます.
ハザード関数を表す項のうち,基準ハザード関数 $${h_0(t)}$$ のみが時間に依存する一方で,共変量に関する項 $${\exp({\sum^{p}_{i=1} \beta_i X_i})}$$ は時間には依存しません.そして,「異なる共変量をもつ2つの対象のハザード関数の比は時間に依らず一定である」というのが比例ハザード仮定の意味するところでした.
$${\frac{h(t, X)}{h(t, X^*)} = \frac{\exp({\sum^{p}_{i=1} \beta_i X_i})}{\exp({\sum^{p}_{i=1} \beta_i X^{*}_{i}})} = \exp({\sum^{p}_{i=1} \beta_i (X_i - X^{*}_{i})}) = constant}$$
比例ハザード仮定が成立する場合,ある固定時点 $${t}$$ におけるイベントの発生確率(時間で条件づけた発生確率)の違いは共変量のみに依存します.つまり,ある時点においてイベントが発生した対象とそうでない集団のイベントの発生有無を決定づけたのは共変量の違い(差)ということになります.
Shoenfeld 残差は「ある時点 $${t_{i}}$$ において,イベントを起こした対象 $${i \in D}$$ の共変量 $${X_{i \xi}}$$ とそうでない生存集団の共変量の期待値 $${A_{i \xi}(\bm{\beta})}$$ との差」ですが,もし比例ハザード仮定が成立するのであれば,「Shoenfeld 残差はイベントの発生した時間に関わらず,多少のばらつきはあってもおおよそ一定になっていそう」です.言い換えれば「Shoenfeld 残差がイベントの発生した時間に伴うなんらかの変化パターンをもっているような場合,比例ハザード仮定を破っていそう」ということになります.この説明は少し飛躍気味で直感的な洞察にすぎませんが,より論理的にこのあたりを追いかけてみたい方は Shoenfeld 残差の原論文を読むことをお勧めします.(https://www.jstor.org/stable/2335876)以上のことから分かる重要な点をまとめておきます.
- Shoenfeld 残差は各対象 $${i}$$ のイベントが発生した時点 $${t_i}$$ で各共変量において定義される $${X_{i \xi} - A_{i \xi}(\bm{\beta})}$$ だが,比例ハザード仮定が成立するのであれば,時間($${t}$$)にともなう変化のパターンをもっていないはずである.
- また,係数 $${\bm{\beta}}$$ は Cox 尤度による推定値であり,下式から計算される.
$${\sum_{i \in D} \bigl( X_{i \xi} - A_{i \xi}(\bm{\beta}) \bigr) = 0}$$
これは,Shoenfeld 残差を全イベント発生時点で合計するとゼロになることを意味する.
- したがって,ある共変量において Cox 比例ハザード仮定が満たされている場合,時間を横軸にその共変量の Shoenfeld 残差を縦軸にプロットした場合,Shoenfeld 残差は明確な時間的なパターンをもたず,望ましくはゼロ付近に正負に渡って散布しているはずである.
如何でしょうか.Shoenfeld 残差というものがどういうものか何となくイメージがついたかと思いますので,次は R で実際に残差をプロットしてみましょう.
2. R による Shoenfeld 残差
前回記事と同様に survival パッケージ内の cancer データを使用して, Shoenfeld 残差をプロットしてみます.
まず最初にデータ整形を行いますが,前回記事と全く同じ手順ですのでデータの詳細など諸々の解説は省略します.
cancer <- survival::cancer %>%
filter(!is.na(ph.ecog) & ph.ecog < 2) %>%
mutate(
status = ifelse(status == 1, yes = 0, no = 1),
sex = factor(sex, levels = c(1, 2), labels = c("M", "F")),
ph.ecog = as.factor(ph.ecog)
)次に,survival::Surv 関数で作成した Surv オブジェクトを使い,survival::coxph 関数で Cox-PH モデルの fitting を行います.この手順は第4回の記事内で解説しましたので,忘れてしまった方は振り返ってみてください(https://note.com/maxwell/n/nbb9dfb507040).
surv.obj <- Surv(time = cancer$time, event = cancer$status)
cox.m.1 <- coxph(formula = surv.obj ~ sex,
data = cancer,
ties = "efron")R の場合,Shoenfeld 残差を計算するための residuals.coxph 関数が survival パッケージから提供されています.実際は総称的関数である residuals 関数でこの関数を呼び出すことができますので,以下のように coding してあげれば良いです.
cox.m.1.res <- residuals(cox.m.1, type = "schoenfeld")
cat(sum(cox.m.1.res)) # -1.758954e-07type 引数には, "martingale", "deviance", "score", "schoenfeld", "dfbeta"', "dfbetas", "scaledsch", "partial" と多くの residuals type を指定することができますが,ここでは本題に沿って "Schoenfeld" を指定しています.
また,計算した残差の総和を計算してみるとほぼゼロになっていることからも「Shoenfeld 残差を全イベント発生時点で合計するとゼロになる」ことを確認できます.
作成した cox.m.1.res オブジェクトをデータフレームに変換し Shoenfeld 残差をプロットするには以下のようにします.
cox.m.1.res.df <- tibble(time = names(cox.m.1.res), sex = cox.m.1.res) %>%
mutate(time = as.numeric(time))
p1 <- ggplot(data = cox.m.1.res.df, aes(x = time, y = sex)) +
geom_point(color = col.plos.pink, size = 1, alpha = 0.75) +
geom_smooth(method = "loess", span = 1, se = FALSE, size = 0.5, color = col.os) +
labs(y = "Schoenfeld residuals for sex variable")
p1尚,geom_smooth 関数を使い loess 曲線も合わせて描画しています.
その結果,下のようなプロットが得られます.

結果をいくつかのポイントを交えて簡単に解釈してみましょう.
sex 変数は男女を表す変数で二値変数にした場合,0 か 1 の値をとります(男: 0,女:1).cancer データをみてみれば分かりますが,一番最初にイベントが発生する対象は女性で sex 変数では 1 に該当し,時間 $${5}$$ で発生しています.この時,リスクセットにおける sex 変数の平均値は男性の方が多く約 $${0.4}$$ となっています.Shoenfeld 残差の計算に使用されるリスクセットにおける sex 変数の期待値は「イベント発生確率をもとにした加重平均」で計算されますので $${1 - 0.4 = 0.6}$$ とはなりませんが,少なくとも Shoenfeld 残差は正の値になることが予想されます.一方で,イベントが発生した対象が男性の場合は sex 変数は 0 であり,Shoenfeld 残差は負の値になることが予想されます.実際に上図では,女性と男性のそれぞれに対応した2つの水平プロットが正と負の領域それぞれに存在していることからもこの考えが正しいことが確認できます.
また,時間 $${300}$$ あたりまでは loess 曲線はほぼ平らで(loess 回帰における span パラメータの値次第で見え方が変わる点には留意が必要),比例ハザード仮定が成り立っていそうです.一方で,時間 $${500}$$以降は loess 曲線は段々と正の方向へとシフトしており,少なくとも見た感じでは比例ハザード仮定の成立に疑問が残ります.
定性的な解釈になってしまっていますが,この点を仮説検定を使って定量的に評価するのが次回となります.
ここまでは Shoenfeld 残差をみてきましたが,シンプルな Shoenfeld 残差 とならびよく使用されるものに Scaled Shoenfeld 残差 というものがあります.
Scaled Shoenfeld 残差は,"Scaled" とある通り Shoenfeld 残差をスケーリングしたものです.Shoenfeld 残差を求める際に $${A_{i \xi}(\bm{\beta})}$$ を計算しましたが,これは対象 $${i}$$ にイベントが発生した時のリスクセットにおける共変量 $${X_{\xi}}$$ の期待値でした.期待値を求める時と同じような形で,共変量ベクトルの直積の各要素に対しても同様の演算をすることで,各イベント発生時点における共変量ベクトル $${\bm{X}}$$ の共分散行列を求めることができます.そして,Scaled Shenfeld 残差はこの共分散行列の逆行列を Shoenfeld 残差ベクトルにかける(スケーリングに該当)ことで求められます.
次回の内容とも関連しますが,なぜこのようなスケーリングをするのかという点に関しても説明しておきます.
比例ハザード仮定の成立を帰無仮説とし,係数ベクトルが時間変化することを,
$${\beta(t) = \beta + G(t) \theta}$$
とした場合,対立仮説は $${\theta \neq 0}$$ となります.
ここで結果だけ述べますが,Scaled Shoenfeld 残差($${ssr(\beta)}$$)の期待値は,
$${E [ssr(\beta)] \sim G(t) \theta}$$
となります.要は,Scaled Shoenfeld 残差の期待値は係数ベクトルの時間変化分に近似的に等しいわけです.よって,もし比例ハザード仮定が棄却されるのであれば,Scaled Shoenfeld 残差の期待値もゼロにはならないことになります.
以上は簡略化した説明ですので,理論的な背景をより詳しく知りたい方は以下の論文を読んでみるとよいでしょう.
Grambsch, Patricia M., and Terry M. Therneau. 1994. “Proportional Hazards Tests and Diagnostics Based on Weighted Residuals.” Biometrika 81(3): 515–26. https://www.jstor.org/stable/2337123
R では,Scaled Shoenfeld 残差の計算とプロットを一気に行ってくれる便利な survminer::ggcoxzph 関数があり,例えば以下のような code で簡単に描画することができます.
p1.s <- ggcoxzph(
fit = cox.zph(fit = cox.m.1),
resid = TRUE, se = TRUE, df = 3, nsmo = length(cox.m.1.res),
var = "sex",
point.col = col.plos.pink, point.size = 1, point.shape = 19, point.alpha = 0.75,
caption = NULL,
ggtheme = theme(
title = element_blank(),
axis.title = element_text(face = font.face, color = col.os),
axis.text = element_text(face = font.face, color = col.os),
panel.grid.major = element_line(size = 0.25),
panel.grid.minor = element_blank()
)
)
attr(p1.s, "global_pval") <- NULL
p1.s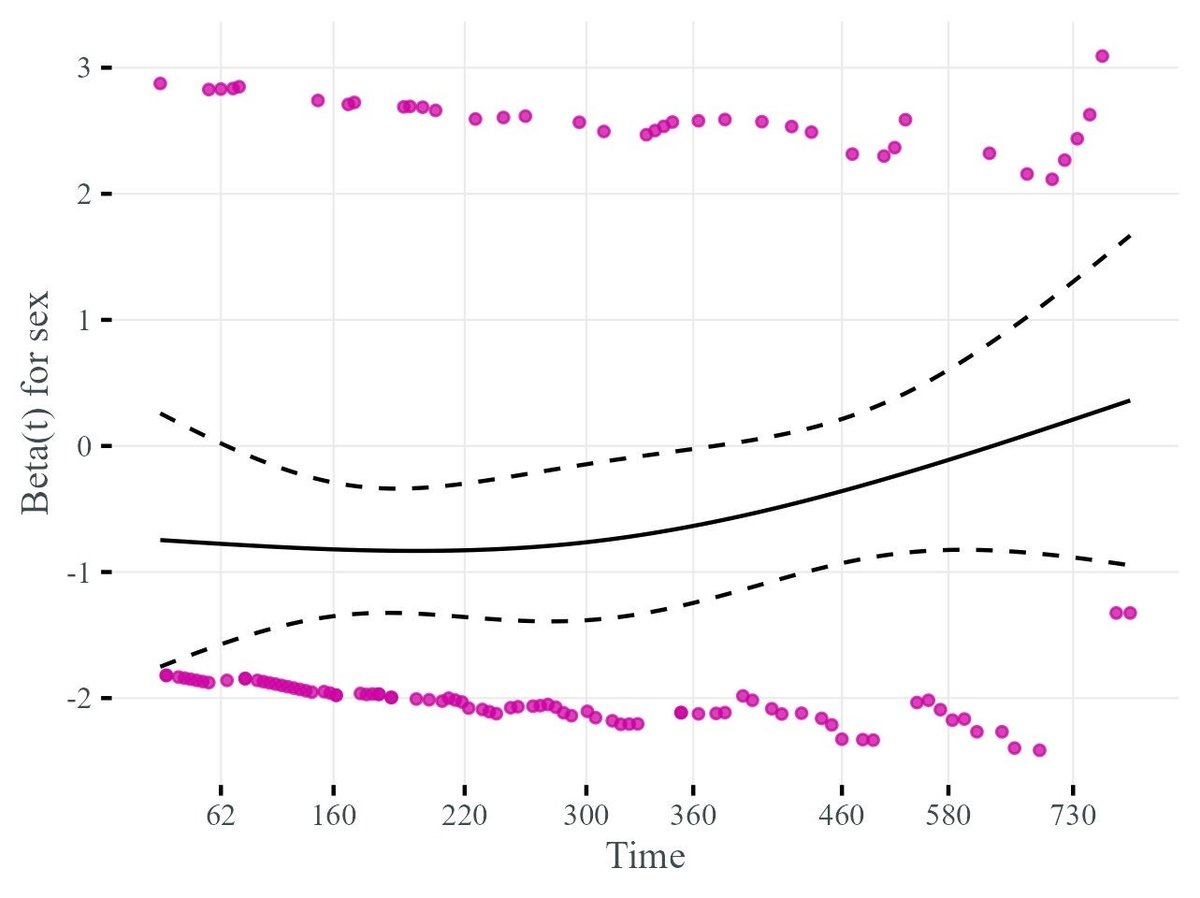
デフォルトでプロットされる縦軸のラベルをみてみると,「Beta(t) for sex」とあります.先程の説明の通り,Scaled Shoenfeld 残差の期待値は係数ベクトルの時間変化に近似的に一致しますので,Scaled Shoenfeld 残差を求めた上で Cox PH モデルで求めた係数 $${\beta}$$ を足してあげれば,時間変化すると仮定した場合の $${\beta(t)}$$ を近似的に求めることができます.なので,ggcoxzph 関数で Scaled Shoenfeld 残差をプロットしたつもりにも関わらず,縦軸のラベル名は「Beta(t) for sex」となっているのです.
また,二値変数のように水平方向にそれぞれの群に分かれた形で残差がプロットされてしまうような場合は,それだけみていても時間的傾向がよく分かりません.こういった時は,loess 回帰などを使った smoothed fitting 曲線を描くことで $${\beta(t)}$$ の時間的変化を検証するのがより有効になります.上図では fitting 曲線の信頼区間を ggcoxzph 関数の se 引数(=TRUE)で追加描画していますが,信頼区間内には一つの点も存在していません.これは時間的傾向が有意とはいえないことを示唆しています.
さて,ggcoxzph 関数はとても便利ですが一点だけ注意があります.本記事の執筆時点(May. 23)で CRAN に登録されている survminer の version は信頼区間の計算・表示にバグを抱えており,異様に広い信頼区間を表示するようになってしまっているようです.
ですので,下記のように github 上の開発バージョンをインストールしてあげるようにしましょう.
devtools::install_github("kassambara/survminer", build_vignettes = FALSE)こうすることで,上図のように正しい信頼区間が表示されるはずです.
気がつくとまた長めの内容になってしまいましたが,今回は次回の比例ハザード仮定の仮説検定に必要となる Shoenfeld 残差をみてきました.
それでは,また次回お会いしましょう.
Until next time!
3. Codes
今回使用したコードは以下となります.
https://github.com/Greenwind1/survival-analysis/blob/master/src/note_06.R
4. References
Schoenfeld, David. 1982. “Partial Residuals for The Proportional Hazards Regression Model.” Biometrika 69(1): 239–41.
https://www.jstor.org/stable/2335876
Grambsch, Patricia M., and Terry M. Therneau. 1994. “Proportional Hazards Tests and Diagnostics Based on Weighted Residuals.” Biometrika 81(3): 515–26.
https://www.jstor.org/stable/2337123
本シリーズの内容の多くは「エモリー大学クラインバウム教授の生存時間解析(サイエンティスト社)」にもとづいたものとなっていますので,より詳しく勉強されたい方は合わせてそちらを読んでみることもお勧めします.
この記事が気に入ったらサポートをしてみませんか?
