
高校数学をプログラミングで解く(数学B編)「4-10 推定」
マガジンリスト > 数学B編 4.確率分布と統計的な推測 > 4-10 推定
はじめに
今回は、数学Bで学ぶ「推定」について、母平均$${m}$$または母比率$${p}$$に対する信頼度 95 %の信頼区間を解説し、プログラムで信頼区間を求めるプログラムを作成します。
推定
まず、推定について解説しておきます。
標本の大きさ$${n}$$が十分大きいものとします。
母平均$${m}$$の推定
標本平均を$${\bar{X}}$$、母標準偏差を$${\sigma}$$($${\sigma}$$の代わりに標本標準偏差$${s}$$を用いてもよい)とすると、母平均$${m}$$に対する信頼度 95 %の信頼区間は
$$
\left[ \bar{X} - 1.96 \cdot \frac{\sigma}{\sqrt{n}}, \bar{X}+1.96 \cdot \frac{\sigma}{\sqrt{n}} \right]
$$
母比率$${p}$$の推定
標本のある性質を満たすものの比率(標本比率)を$${R}$$とすると、母比率$${p}$$に対する信頼度 95 %の信頼区間は
$$
\left[ R - 1.96 \sqrt{ \frac{R(1-R)}{n}}, R + 1.96 \sqrt{ \frac{R(1-R)}{n}} \right]
$$
「信頼度 95 %の信頼区間」とは
「信頼度 95 %の信頼区間」の意味について、間違えて理解している人は多いようです。そこで、統計学についてまとめてあるサイト「統計WEB - 統計学、調べる、学べる、BellCurve(ベルカーブ)」の「19-3. 95%信頼区間のもつ意味 | 統計学の時間 | 統計WEB (bellcurve.jp)」のページにわかりやすい解説がありましたので、それを参考に「信頼度 95 %の信頼区間」について説明しておきます。
「信頼度 95 %の信頼区間」は、「正規分布に従う母集団から標本を取ってきてその標本平均または標本比率から信頼度 95 %の信頼区間を求めた時に、その区間の中に 95 %の確率で母平均または母比率が含まれる」という意味ではありません。正しくは、「母集団から標本を取ってきて、その標本平均または標本比率から信頼度 95 %の信頼区間を求める、という作業を100回やったときに、95回はその区間の中に母平均または母比率が含まれる」という"頻度"もしくは"割合"を意味します。
「1.96」ってどこから出てきた?
もう一つ気になるのは、「1.96」という数がどこから出てきたかということだと思います。これを見るために、「信頼度 95 %の信頼区間」を実際に導出してみます。
記事『高校数学をプログラミングで解く(数学B編)「4-9 標本平均の分布」』で、標本平均$${\bar{X}}$$の分布について、母集団が正規分布$${N(m,\sigma^2)}$$に従うとき、$${\bar{X}}$$も正規分布に従い、どのような母集団でも、$${n}$$が大きいときは、正規分布$${N(m, \sigma^2/n)}$$に従うことを説明しました。
このことを利用して、標本平均$${\bar{X}}$$を
$$
Z = \frac{\sqrt{n}(\bar{X}-m)}{ \sigma}
$$
と変数変換すると、この$${Z}$$は$${n}$$が大きいとき標準正規分布$${N(0,1)}$$に従う確率変数となります。
次に、標準正規分布から確率$${P(-a \leq Z \leq a) = 0.95}$$となるような確率変数$${Z}$$の値$${a}$$を求めます。つまり、図1に示したように、標準正規分布の確率密度関数で中心($${z=0}$$)から左右に全体の95%の面積(青色の領域)となるように$${a}$$を決めます。この$${a}$$の値は正規分布表などから算出することができ、「1.96」となります。(また、記事『高校数学をプログラミングで解く(数学B編)「4-7 正規分布」』で標準正規分布から確率$${P(a \leq X \leq b)}$$を計算するためのプログラム(スケッチ「normaldistribution」)を作成しているので、これに積分範囲を$${[-1.96,1.96]}$$と指定して、確率$${P(-1.96 \leq X \leq 1.96)}$$が 0.95 となるか確かめてみるのもよいと思います。)

この結果から、「信頼度 95 %の信頼区間」は、
$$
-1.96 \leq Z \leq 1.96
$$
となります。最後に、$${Z}$$を$${\bar{X}}$$に戻すと、
$$
\bar{X} - 1.96 \cdot \frac{\sigma}{\sqrt{n}} \leq m \leq \bar{X}+1.96 \cdot \frac{\sigma}{\sqrt{n}}
$$
となり、母平均$${m}$$に対する信頼度 95 %の信頼区間が得られます。
母平均 m の推定を行う
今回は母平均$${m}$$の推定を行う例として、以下の問題を考えてみます。
問題1
ある試験を受けた高校生の中から、100人を任意に選んだところ、平均点は 58.3 点であった。母標準偏差を 13.0 点として、母平均の信頼区間を信頼度 95 %で求めよ。
アルゴリズム設計
この問題は、$${n=100}$$、$${\bar{X}=58.3}$$、$${\sigma = 13.0}$$として
$$
\bar{X} - 1.96 \cdot \frac{\sigma}{\sqrt{n}}
$$
と
$$
\bar{X} + 1.96 \cdot \frac{\sigma}{\sqrt{n}}
$$
とを計算するだけで母平均$${m}$$に対する信頼度 95 %の信頼区間を求めることができますので、プログラミングする必要もないのですが、今回はあえてプログラムを作成します。
プログラム
母平均$${m}$$に対する信頼度 95 %の信頼区間を求めるプログラムを作成します。
// 母平均の推定
void setup(){
// 標本の大きさ
int n = 100;
// 標本平均
float bar_X = 58.3;
// 母標準偏差
float sigma = 13.0;
// 標準正規分布の上側2.5%点
float u = 1.96;
// 信頼区間の下限
float confidence_interval_lower = bar_X - u * sigma / sqrt(n);
// 信頼区間の上限
float confidence_interval_upper = bar_X + u * sigma / sqrt(n);
// 母平均に対する信頼度 95 %の信頼区間を
// コンソールに出力する
println("[" + confidence_interval_lower + ", " + confidence_interval_upper + "]");
}ソースコード1 母平均$${m}$$に対する信頼度 95 %の信頼区間を求めるプログラム
このソースコードを、Processingの開発環境ウィンドウを開いて(スケッチ名を「estimatePopulationMean」としています)、テキストエデ
ィタ部分に書いて実行します。

図2のように、問題1の母平均$${m}$$に対する信頼度 95 %の信頼区間を
[55.752, 60.848]
とコンソールに出力します。
母比率 p の推定を行う
次に母比率$${p}$$の推定を行う例として、以下の問題を考えてみます。
問題2
ある工場で生産している電球の中から 800 個を無作為抽出して検査したところ、不良品が 32 個あった。この製品全体の不良率を信頼度 95 %で推定せよ。
アルゴリズム設計
まず、800 個のうち32個の不良品があったということなので、標本比率$${R=32/800}$$となります。あとは、$${n=800}$$として
$$
R - 1.96 \sqrt{ \frac{R(1-R)}{n}}
$$
と
$$
R + 1.96 \sqrt{ \frac{R(1-R)}{n}}
$$
とを計算するだけで母比率$${p}$$に対する信頼度 95 %の信頼区間を求めることができますので、この問題もプログラミングする必要ないですが、今回はあえてプログラムを作成します。
プログラム
母比率$${p}$$に対する信頼度 95 %の信頼区間を求めるプログラムを作成します。
// 母比率の推定
void setup(){
// 標本の大きさ
int n = 800;
// 不良品の数
int defective = 32;
// 標本比率
float R = (float)defective / n;
// 標準正規分布の上側2.5%点
float u = 1.96;
// 信頼区間の下限
float confidence_interval_lower = R - u * sqrt( R*(1.0-R)/n );
// 信頼区間の上限
float confidence_interval_upper = R + u * sqrt( R*(1.0-R)/n );
// 母比率に対する信頼度 95 %の信頼区間を
// コンソールに出力する
println("[" + confidence_interval_lower + ", " + confidence_interval_upper + "]");
}ソースコード2 母比率$${p}$$に対する信頼度 95 %の信頼区間を求めるプログラム
このソースコードを、Processingの開発環境ウィンドウを開いて(スケッチ名を「estimatePopulationRate」としています)、テキストエデ
ィタ部分に書いて実行します。
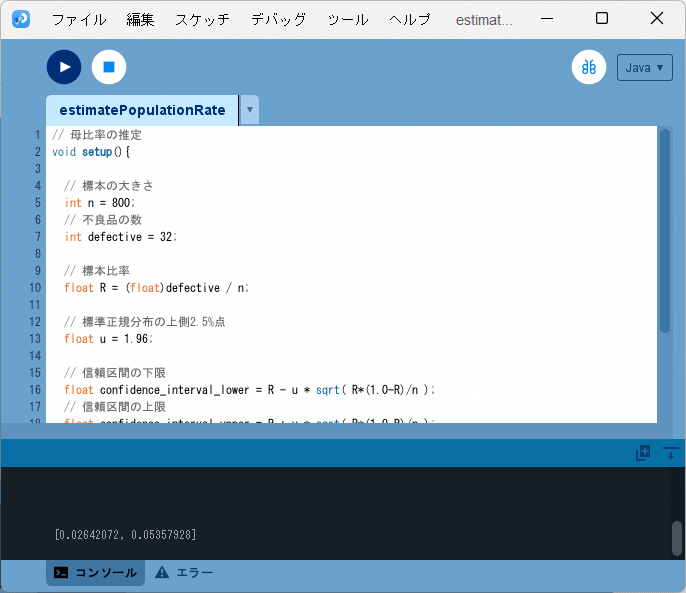
図3のように、問題2の母比率$${p}$$に対する信頼度 95 %の信頼区間を
[0.02642072, 0.05357928]
とコンソールに出力します。
まとめ
今回は、数学Bで学ぶ「推定」について、母平均$${m}$$または母比率$${p}$$に対する信頼度 95 %の信頼区間を解説し、プログラムで信頼区間を求めるプログラムを作成しました。
「信頼度 95 %の信頼区間」という概念は、少し理解するのが難しいかもしれません。参考文献に挙げているサイトなどを参考にして、頭の中を整理して理解に努めてみてください。
参考文献
改訂版 教科書傍用 スタンダード 数学B(数研出版、ISBN9784410209468)
統計学についてまとめてあるサイト「統計WEB - 統計学、調べる、学べる、BellCurve(ベルカーブ)」
この記事が気に入ったらサポートをしてみませんか?
