高校数学をプログラミングで解く（数学B編）「4-7 正規分布」

MK's papa

2024年8月7日 18:00

はじめに

今回は、数学Bで学ぶ「正規分布」について、正規分布をはじめ、いくつかの確率密度関数による確率や期待値、分散などを計算するプログラムを作成します。

連続型確率変数の分布、正規分布

まず、連続型確率変数とその分布、及び正規分布について解説しておきます。

連続型確率変数とその分布

$${X}$$を連続型確率変数、曲線$${y=f(x)}$$を$${X}$$の分布曲線とするとき、確率密度関数$${f(x)}$$には、次の性質がある。

$$
\mathrm{常に} f(x) \geq 0
$$

$$
P(a \leq X \leq b)= \int_a^b f(x) dx
$$

$$
\alpha \leq X \leq \beta \mathrm{のとき} \int_{\alpha}^{\beta} f(x) dx = 1
$$

期待値

$$
E(X) = m = \int_{\alpha}^{\beta} xf(x)dx
$$

分散

$$
V(X) = \int_{\alpha}^{\beta}(x-m)^2 f(x) dx
$$

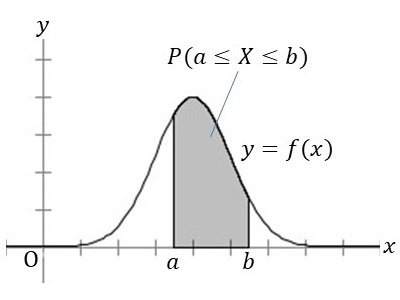
正規分布

$${X}$$が正規分布$${N(m,\sigma^2)}$$に従う確率変数であるとき

確率密度関数

$$
f(x) = \frac{1}{\sqrt{2\pi} \sigma} e^{-\frac{(x-m)^2}{2 \sigma^2}}
$$

期待値

$$
E(X) = m
$$

標準偏差

$$
\sigma(X) = \sigma
$$

確率、期待値、分散を計算する方法

以下で、確率密度関数や標準正規分布による確率や期待値、分散などを上記の定義に沿って計算していきますので、その方法についてまとめておきます。

確率密度関数による確率の計算

確率密度関数による確率$${P(a \leq X \leq b)}$$は、

$$
P(a \leq X \leq b)= \int_a^b f(x) dx
$$

のように定積分で表されます。この定積分をコンピュータで数値的に計算していくために、定積分の計算方法のひとつである台形公式を利用します。

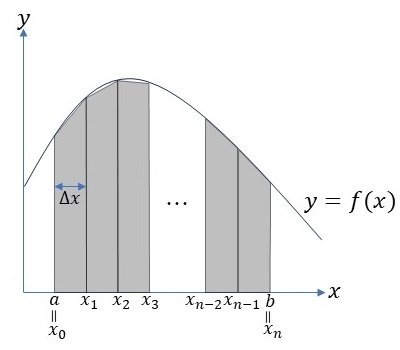
台形公式は、図2のように関数$${f(x)}$$の$${a}$$から$${b}$$までの積分領域を$${n}$$個の部分に分割し、分割した各部分の面積を台形の面積で近似して足し合わせることで定積分の値を計算する方法です。

具体的には、まず$${\Delta x}$$を積分範囲の大きさ$${b-a}$$と比較して十分小さな値をもつ定数で、かつ

$$
n= \frac{b-a}{\Delta x}
$$

が整数となるように、調整して決めます。このようにして決めた$${\Delta x}$$を用いると、$${x_i}$$は、

$$
x_i = a +i\Delta x \ \ (i=0,1,2,\cdots,n)
$$

となります。なお、$${x_0 = a, \ \ x_n = b}$$となります。このとき、図2の分割した各部分を台形で近似したときの面積は

$$
\frac{1}{2} (f(x_i)+f(x_{i+1})) \Delta x \ \ (i=0,1,2,\cdots,n-1)
$$

と計算することができます。したがって、確率$${P(a \leq X \leq b)}$$は、

$$
P(a \leq X \leq b)= \int_a^b f(x) dx = \sum_{i=0}^{n-1} \left[ \frac{1}{2} (f(x_i)+f(x_{i+1})) \Delta x \right]
$$

で計算することができます。

確率密度関数による期待値の計算

次に、確率密度関数による期待値

$$
E(X) = m = \int_{\alpha}^{\beta} xf(x)dx
$$

の計算を考えます。こちらも台形公式を用いてコンピュータで数値的に計算することができます。つまり、$${x_0=\alpha, x_n = \beta}$$となるように$${\Delta x}$$と整数$${n}$$を決めると、

$$
E(X) = m = \sum_{i=0}^{n-1} \left( x_i + \frac{\Delta x}{2} \right) \left[ \frac{1}{2} (f(x_i)+f(x_{i+1})) \Delta x \right]
$$

で計算することができます。なお、今回被積分関数$${xf(x)}$$の$${x}$$については、分割した各積分範囲$${[x_i, x_{i+1}]}$$の中点

$$
\frac{x_i+x_{i+1}}{2} = x_i + \frac{\Delta x}{2}
$$

で近似するようにしています。

確率密度関数による分散の計算

最後に、確率密度関数による分散

$$
V(X) = \int_{\alpha}^{\beta}(x-m)^2 f(x) dx
$$

の計算を考えます。これは、上記の確率や期待値の計算と同じように台形公式を用いてコンピュータで数値的に計算することができます。

$$
V(X) = \sum_{i=0}^{n-1} \left( x_i + \frac{\Delta x}{2} - m \right)^2 \left[ \frac{1}{2} (f(x_i)+f(x_{i+1})) \Delta x \right]
$$

以上のことを踏まえて、以下で具体的にいくつかの簡単な確率密度関数による確率や期待値、分散などを計算するプログラムを作成していきます。

定数の確率密度関数による確率、期待値の計算

次のような問題を考えてみます。

問題1
確率変数$${X}$$の確率密度関数$${f(x)}$$が、

$$
f(x) = \frac{1}{2} (0 \leq x \leq 2)
$$

で表されるとき、確率$${P(0 \leq X \leq 1)}$$、期待値、分散、標準偏差を求めよ。

アルゴリズム設計

問題1は、定数の確率密度関数ですので、確率や期待値、分散の計算は手計算で簡単に求めることができますが、今回は敢えて上記で説明した台形公式を利用して計算することにします。

プログラム

問題1の確率$${P(0 \leq X \leq 1)}$$、期待値、分散、標準偏差を計算するプログラムを作成します。なお、今回は、確率密度関数とその確率密度関数から計算される確率$${P(0 \leq X \leq 1)}$$の範囲を示した図も実行ウィンドウのキャンバスに表示されるようにしています。

// 定数の確率密度関数による確率の計算
void setup(){
  size(500,500);
//  background(255,255,255);
  noLoop();
  float x_range = 4.0; // x軸の表示範囲 -x_rangeからx_rangeまで
  float y_range = 1.0; // y軸の表示範囲 -y_rangeからy_rangeまで 
  setAxes(x_range, y_range); // 座標軸の準備
  

  noFill();
  stroke(0,0,0);
  
  // グラフの定義域
  float x_l = -x_range; // 定義域の左端
  float x_r = x_range; // 定義域の右端
  int plot_num = 2000; // グラフを描くための頂点の個数  
  
  // グラフを描画
  float x, y; // 関数の座標
  float X, Y; // キャンバス上の座標 
  beginShape();
  for(int i=0; i<=plot_num; i++){
    x = x_l + (x_r - x_l) / plot_num * i; // 関数のx座標
    y = constant_PDF(x); // 関数の値
    // キャンバス上の座標位置に換算
    X = width / 2.0 / x_range * x;
    Y = height / 2.0 / y_range * y;
    vertex(X, Y);
  }
  endShape();

  // P(0≦X≦1)の領域を青色で塗りつぶす
  fill(0,0,255,64);
  float a = 0.0;
  float b = 1.0;
  beginShape();
  y = constant_PDF(a);
  X = width / 2.0 / x_range * a;
  Y = height / 2.0 / y_range * y;
  vertex(X, 0.0);
  vertex(X, Y);
  for(int i=0; i<=plot_num; i++){
    x = a + (b - a) / plot_num * i; // 関数のx座標
    y = constant_PDF(x); // 関数の値
    // キャンバス上の座標位置に換算
    X = width / 2.0 / x_range * x;
    Y = height / 2.0 / y_range * y;
    vertex(X, Y);
  }
  vertex(X, 0.0);
  endShape(CLOSE); 

  // P(0≦X≦1)の値を計算する
  float prob = probability_of_constant_PDF(a,b);
  println("確率P(0≦X≦1)：", prob);

  // 期待値の計算
  float m = expectation_value_of_constant_PDF();
  println("期待値:",m);
  
  // 分散の計算
  float v = variance_of_constant_PDF(m);
  println("分散：", v);
  
  // 標準偏差の計算
  float sd = sqrt(v);
  println("標準偏差：",sd);

}

// 定数の確率密度関数
float constant_PDF(
  float x
){
  float value;
  if(x >= 0.0 && x <= 2.0){
    value = 1.0/2.0;
  } else {
    value = 0.0;
  }
  return value;
}

// 定数の確率密度関数による確率P(a≦X≦b)を計算する関数（台形公式を利用）
float probability_of_constant_PDF(
  float a, // 積分領域の下限
  float b // 積分領域の上限
){
  float dx = 0.01;
  int division_num = (int)((b-a)/dx);
  float x, y1, y2;
  float prob = 0.0;
  for(int i=0; i<division_num; i++){
    x = a + i*dx;
    y1 = constant_PDF(x);
    y2 = constant_PDF(x+dx);
    prob = prob + (y1+y2)*dx/2.0;
  }
  return prob;
}

// 定数の確率密度関数による期待値を計算する関数（台形公式を利用）
float expectation_value_of_constant_PDF(){
  float dx = 0.01;
  float a = 0.0;
  float b = 2.0;
  int division_num = (int)((b-a)/dx);
  float x, y1, y2;
  float m = 0.0;
  for(int i=0; i<division_num; i++){
    x = a + i*dx;
    y1 = constant_PDF(x);
    y2 = constant_PDF(x+dx);
    m = m + (x+dx/2.0)*(y1+y2)*dx/2.0;
  }
  return m;
}

// 定数の確率密度関数による分散を計算する関数（台形公式を利用）
float variance_of_constant_PDF(
  float m // 期待値
){
  float dx = 0.01;
  float a = 0.0;
  float b = 2.0;
  int division_num = (int)((b-a)/dx);
  float x, y1, y2;
  float v = 0.0;
  for(int i=0; i<division_num; i++){
    x = a + i*dx;
    y1 = constant_PDF(x);
    y2 = constant_PDF(x+dx);
    v = v + (x+dx/2.0-m)*(x+dx/2.0-m)*(y1+y2)*dx/2.0;
  }
  return v;
}

ソースコード1　定数の確率密度関数による確率$${P(0 \leq X \leq 1)}$$、期待値、分散、標準偏差を計算するプログラム

スケッチ「probability_PDF1」を準備し、その「probability_PDF1」フォルダに記事『高校数学をプログラミングで解く（数学I編）「1-0-1 グラフを描くための準備（その1）」』及び『高校数学をプログラミングで解く（数学I編）「1-0-2 グラフを描くための準備（その2）」』で作成した「setAxes.pde」ファイルをコピーして、ソースコード1を、「probability_PDF1」タブのテキストエディタ部分に書いて実行すると、図3のように、

確率P(0≦X≦1)： 0.49999967
期待値: 1.0
分散： 0.33332494
標準偏差： 0.577343

とコンソールに出力されます。なお、これらを手計算で行ったときの結果は、

$$
\mathrm{確率:} \frac{1}{2} \mathrm{、期待値:}1 \mathrm{、分散:} \frac{1}{3} \mathrm{、標準偏差:} \frac{1}{\sqrt{3}}
$$

となるので、おおむね正しい結果が得られていることがわかります。

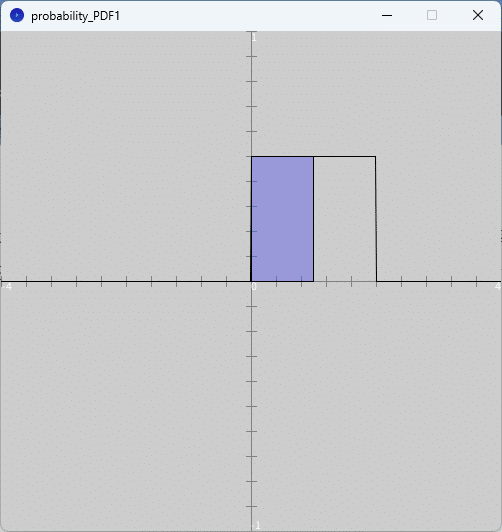
また図4のように、実行ウィンドウのキャンバスに確率密度関数とその確率密度関数から計算される確率$${P(0 \leq X \leq 1)}$$の範囲を示した図が示されます。なお、$${x}$$軸方向は$${[-4,4]}$$、$${y}$$軸方向は$${[-1,1]}$$の範囲でグラフを表示していることに注意してください。

プログラムの解説

確率密度関数の定義
確率密度関数$${f(x)}$$は関数名を「constant_PDF」、引数を連続型確率変数 x (float型）、返り値を連続型確率変数の値 x に対する確率密度の値（float型）、となるような関数として準備しました。なお、今回の定数の確率密度関数$${f(x)}$$は、

$$
\begin{array}{}
f(x) =
\begin{cases}
1/2 & 0 \leq x \leq 2 \\
0 & \mathrm{その他}
\end{cases}
\end{array}
$$

と書くことができるので、この形で関数 constant_PDF を作成しています。

確率密度関数のグラフ
確率密度関数のグラフを描く方法は、記事『記事『高校数学をプログラミングで解く（数学I編）「1-0-1 グラフを描くための準備（その1）」』及び『高校数学をプログラミングで解く（数学I編）「1-0-2 グラフを描くための準備（その2）」』で説明していますので、そちらをご覧ください。
また、確率$${P(0 \leq X \leq 1)}$$の領域を青色で塗り潰すように描いていますが、この部分もグラフを描く方法と同じように描いています。つまり、積分領域を$${[a,b]}$$とすると、４つの点$${(a,0), (a, f(a)), (b, f(b)), (b,0)}$$を順に結んでできた閉じた領域（ただし、$${(a, f(a))}$$と$${(b, f(b))}$$との間は$${f(x)}$$に沿って結ぶ）を塗り潰すようにしています。

確率、期待値、分散を計算する部分は関数化
確率や期待値、分散を計算する部分は今回それぞれ関数化して利用しました。
確率を計算する関数は関数名を「probability_of_constant_PDF」とし、引数を確率を計算する積分領域の下限 a と上限 b とを指定するようにしています。一方、期待値や分散については積分範囲は$${[\alpha, \beta]}$$に確定しているので、引数は与えず、結果のみを返り値として返すようにしています。

線形の確率密度関数による確率、期待値の計算

今度は、線形の確率密度関数をもつ場合の問題を考えてみます。

問題2
確率変数$${X}$$の確率密度関数$${f(x)}$$が、

$$
f(x) = 2x (0 \leq x \leq 1)
$$

で表されるとき、確率$${P(0.3 \leq X \leq 0.5)}$$、期待値、分散、標準偏差を求めよ。

アルゴリズム設計

問題1と同様、問題2も、線形の確率密度関数ですので、確率や期待値、分散の計算は手計算で簡単に求めることができますが、今回も台形公式を利用して計算することにします。

プログラム

問題2の確率$${P(0.3 \leq X \leq 0.5)}$$、期待値、分散、標準偏差を計算するプログラムを作成します。

// 線形の確率密度関数による確率の計算
void setup(){
  size(500,500);
//  background(255,255,255);
  noLoop();
  float x_range = 3.0; // x軸の表示範囲 -x_rangeからx_rangeまで
  float y_range = 3.0; // y軸の表示範囲 -y_rangeからy_rangeまで 
  setAxes(x_range, y_range); // 座標軸の準備
  

  noFill();
  stroke(0,0,0);
  
  // グラフの定義域
  float x_l = -x_range; // 定義域の左端
  float x_r = x_range; // 定義域の右端
  int plot_num = 2000; // グラフを描くための頂点の個数  
  
  // グラフを描画
  float x, y; // 関数の座標
  float X, Y; // キャンバス上の座標 
  beginShape();
  for(int i=0; i<=plot_num; i++){
    x = x_l + (x_r - x_l) / plot_num * i; // 関数のx座標
    y = linear_PDF(x); // 関数の値
    // キャンバス上の座標位置に換算
    X = width / 2.0 / x_range * x;
    Y = height / 2.0 / y_range * y;
    vertex(X, Y);
  }
  endShape();

  // P(0.3≦X≦0.5)の領域を青色で塗りつぶす
  fill(0,0,255,64);
  float a = 0.3;
  float b = 0.5;
  beginShape();
  y = linear_PDF(a);
  X = width / 2.0 / x_range * a;
  Y = height / 2.0 / y_range * y;
  vertex(X, 0.0);
  vertex(X, Y);
  for(int i=0; i<=plot_num; i++){
    x = a + (b - a) / plot_num * i; // 関数のx座標
    y = linear_PDF(x); // 関数の値
    // キャンバス上の座標位置に換算
    X = width / 2.0 / x_range * x;
    Y = height / 2.0 / y_range * y;
    vertex(X, Y);
  }
  vertex(X, 0.0);
  endShape(CLOSE); 

  // P(0.3≦X≦0.5)の値を計算する
  float prob = probability_of_linear_PDF(a,b);
  println("確率P(0.3≦X≦0.5)：", prob);

  // 期待値の計算
  float m = expectation_value_of_linear_PDF();
  println("期待値:",m);
  
  // 分散の計算
  float v = variance_of_linear_PDF(m);
  println("分散：", v);
  
  // 標準偏差の計算
  float sd = sqrt(v);
  println("標準偏差：",sd);


}

// 線形の確率密度関数
float linear_PDF(
  float x
){
  float value;
  if(x >= 0.0 && x <= 1.0){
    value = 2.0 * x;
  } else {
    value = 0.0;
  }
  return value;
}

// 線形の確率密度関数による確率P(a≦X≦b)を計算する関数（台形公式を利用）
float probability_of_linear_PDF(
  float a, // 積分領域の下限
  float b // 積分領域の上限
){
  float dx = 0.01;
  int division_num = (int)((b-a)/dx);
  float x, y1, y2;
  float prob = 0.0;
  for(int i=0; i<division_num; i++){
    x = a + i*dx;
    y1 = linear_PDF(x);
    y2 = linear_PDF(x+dx);
    prob = prob + (y1+y2)*dx/2.0;
  }
  return prob;
}

// 線形の確率密度関数による期待値を計算する関数（台形公式を利用）
float expectation_value_of_linear_PDF(){
  float dx = 0.01;
  float a = 0.0;
  float b = 1.0;
  int division_num = (int)((b-a)/dx);
  float x, y1, y2;
  float m = 0.0;
  for(int i=0; i<division_num; i++){
    x = a + i*dx;
    y1 = linear_PDF(x);
    y2 = linear_PDF(x+dx);
    m = m + (x+dx/2.0)*(y1+y2)*dx/2.0;
  }
  return m;
}

// 線形の確率密度関数による分散を計算する関数（台形公式を利用）
float variance_of_linear_PDF(
  float m // 期待値
){
  float dx = 0.01;
  float a = 0.0;
  float b = 1.0;
  int division_num = (int)((b-a)/dx);
  float x, y1, y2;
  float v = 0.0;
  for(int i=0; i<division_num; i++){
    x = a + i*dx;
    y1 = linear_PDF(x);
    y2 = linear_PDF(x+dx);
    v = v + (x+dx/2.0-m)*(x+dx/2.0-m)*(y1+y2)*dx/2.0;
  }
  return v;
}

ソースコード2　線形の確率密度関数による確率$${P(0.3 \leq X \leq 0.5)}$$、期待値、分散、標準偏差を計算するプログラム

スケッチ「probability_PDF2」を準備し、その「probability_PDF2」フォルダに「setAxes.pde」ファイルをコピーして、ソースコード2を、「probability_PDF2」タブのテキストエディタ部分に書いて実行すると、図5のように、

確率P(0.3≦X≦0.5)： 0.16
期待値: 0.6666499
分散： 0.055552777
標準偏差： 0.23569636

とコンソールに出力されます。なお、これらを手計算で行ったときの結果は、

$$
\mathrm{確率:} 0.16 \mathrm{、期待値:}\frac{2}{3} \mathrm{、分散:} \frac{1}{18} \mathrm{、標準偏差:} \frac{\sqrt{2}}{6}
$$

となるので、おおむね正しい結果が得られていることがわかります。

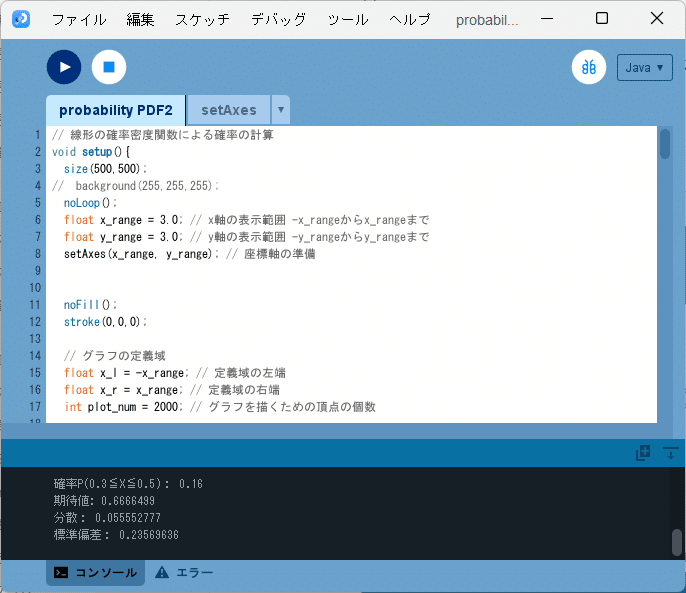
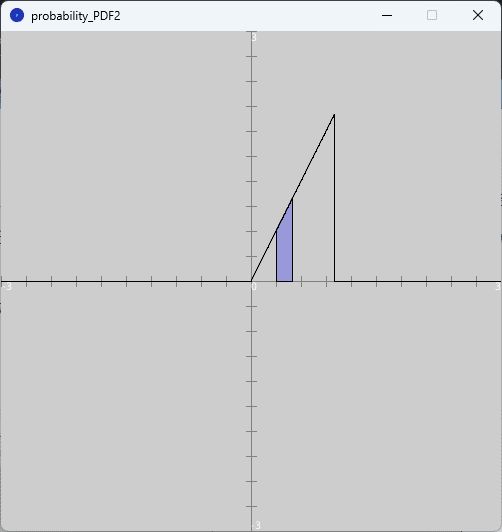
また図6のように、実行ウィンドウのキャンバスに確率密度関数とその確率密度関数から計算される確率$${P(0.3 \leq X \leq 0.5)}$$の範囲を示した図が示されます。なお、$${x}$$軸方向は$${[-3,3]}$$、$${y}$$軸方向は$${[-3,3]}$$の範囲でグラフを表示しています。

標準正規分布による確率の計算

今度は、標準正規分布$${N(0,1)}$$による確率を計算する問題を考えてみます。

問題3
確率変数$${X}$$が標準正規分布$${N(0,1)}$$に従うとき、確率$${P(1 \leq X \leq 2)}$$を求めよ。

アルゴリズム設計

標準正規分布の確率の計算は単純な手計算では難しく、正規分布表などを利用して計算しますが、今回は標準正規分布の確率密度関数

$$
f(x) = \frac{1}{\sqrt{2\pi} } e^{-\frac{x^2}{2}}
$$

をもとに台形公式を利用して計算することにします。

プログラム

問題3の確率$${P(1 \leq X \leq 2)}$$を計算するプログラムを作成します。

// 標準正規分布による確率の計算
void setup(){
  size(500,500);
//  background(255,255,255);
  noLoop();
  float x_range = 5.0; // x軸の表示範囲 -x_rangeからx_rangeまで
  float y_range = 1.0; // y軸の表示範囲 -y_rangeからy_rangeまで 
  setAxes(x_range, y_range); // 座標軸の準備
  

  noFill();
  stroke(0,0,0);
  
  // グラフの定義域
  float x_l = -x_range; // 定義域の左端
  float x_r = x_range; // 定義域の右端
  int plot_num = 200; // グラフを描くための頂点の個数  
  
  // グラフを描画
  float x, y; // 関数の座標
  float X, Y; // キャンバス上の座標 
  beginShape();
  for(int i=0; i<=plot_num; i++){
    x = x_l + (x_r - x_l) / plot_num * i; // 関数のx座標
    y = standard_normal_distribution(x); // 関数の値
    // キャンバス上の座標位置に換算
    X = width / 2.0 / x_range * x;
    Y = height / 2.0 / y_range * y;
    vertex(X, Y);
  }
  endShape();

  // P(1≦X≦2)の領域を青色で塗りつぶす
  fill(0,0,255,64);
  float a = 1.0;
  float b = 2.0;
  beginShape();
  y = standard_normal_distribution(a);
  X = width / 2.0 / x_range * a;
  Y = height / 2.0 / y_range * y;
  vertex(X, 0.0);
  vertex(X, Y);
  for(int i=0; i<=plot_num; i++){
    x = a + (b - a) / plot_num * i; // 関数のx座標
    y = standard_normal_distribution(x); // 関数の値
    // キャンバス上の座標位置に換算
    X = width / 2.0 / x_range * x;
    Y = height / 2.0 / y_range * y;
    vertex(X, Y);
  }
  vertex(X, 0.0);
  endShape(CLOSE); 

  // P(1≦X≦2)の値を計算する
  float prob = probability_of_snd(1.0,2.0);
  println("確率P(1≦X≦2):",prob);


}

// 標準正規分布
float standard_normal_distribution(
  float x
){
  return exp(-x*x /2.0)/sqrt(2.0 * PI);
}

// 標準正規分布による確率P(a≦X≦b)を計算する関数（台形公式を利用）
float probability_of_snd(
  float a, // 積分領域の下限
  float b // 積分領域の上限
){
  float dx = 0.01;
  int division_num = (int)((b-a)/dx);
  float x, y1, y2;
  float prob = 0.0;
  for(int i=0; i<division_num; i++){
    x = a + i*dx;
    y1 = standard_normal_distribution(x);
    y2 = standard_normal_distribution(x+dx);
    prob = prob + (y1+y2)*dx/2.0;
  }
  return prob;
}

ソースコード3　標準正規分布による確率$${P(1 \leq X \leq 2)}$$を計算するプログラム

スケッチ「normaldistribution」を準備し、その「normaldistribution」フォルダに「setAxes.pde」ファイルをコピーして、ソースコード3を、「normaldistribution」タブのテキストエディタ部分に書いて実行すると、図7のように、

確率P(1≦X≦2): 0.13590622

とコンソールに出力されます。なお、この値を正規分布表をもとに計算した結果は、

$$
P(1 \leq X \leq 2) = P(0 \leq X \leq 2) - P(0 \leq X \leq 1) = 0.1359
$$

となるので、おおむね正しい結果が得られていることがわかります。

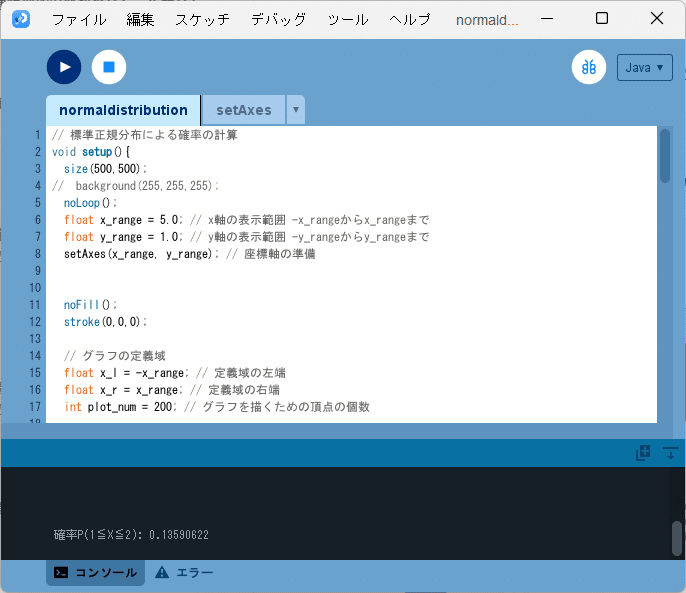
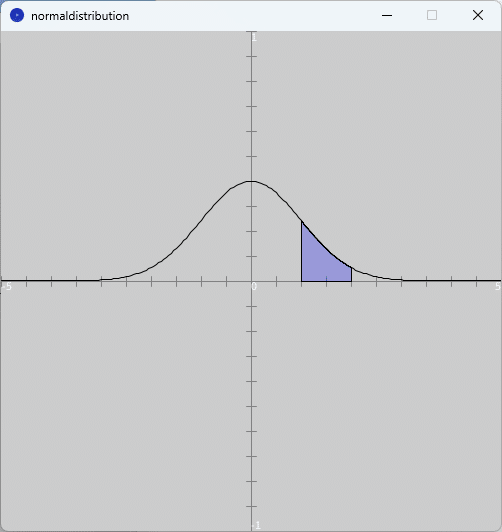
また図8のように、実行ウィンドウのキャンバスに確率密度関数とその確率密度関数から計算される確率$${P(1 \leq X \leq 2)}$$の範囲を示した図が示されます。なお、$${x}$$軸方向は$${[-5,5]}$$、$${y}$$軸方向は$${[-1,1]}$$の範囲でグラフを表示しています。

まとめ

今回は、数学Bで学ぶ「正規分布」について、正規分布をはじめ、いくつかの確率密度関数による確率や期待値、分散などを計算するプログラムを作成しました。
確率密度関数から確率や期待値、分散を計算するときには基本的に定積分を計算する必要があります。今回はこの定積分の値をコンピュータで数値的に計算するために、台形公式を利用してプログラムを作成しました。台形公式は積分領域を分割して、分割した各領域を台形で近似していく方法であるので、分割の幅があまり大きすぎると正しい値との乖離が大きくなってしまいます。そのため、台形公式を利用する場合はこの値の調整をうまく行わなければなりません。このあたりは経験を積んでいくことで少しずつ慣れてくるでしょう。

参考文献

改訂版教科書傍用スタンダード数学B（数研出版、ISBN9784410209468）

この記事が気に入ったらサポートをしてみませんか？