
「ガウスの法則」と「ガウスの定理」
高校で学ぶ物理の電磁気分野で「ガウスの法則」というのが出てきます。電荷と電気力線の本数の間に成り立つ法則です。少し古い教科書や参考書を見ると「ガウスの定理」と書いてある場合もありますが、「ガウスの定理」は電磁気の範囲に限らず、一般的なベクトル場に対して成り立つ数学的な定理を指す、と考えるのが一般的で、電場や電気力線に特化した文脈であれば「ガウスの法則」とすべきでしょう。しかし、「ガウスの法則」と「ガウスの定理」はしばしば混同されます。大学レベルの電磁気学を学んだ人であれば、この二つの違いや関係性を理解するのは難しくないと思いますが、この記事ではそのこと、およびガウスの法則の意味や使い方について解説します。
まず、ガウスの法則は以下のように表現できます:
3次元空間内のある閉曲面 $${ \mathcal{S} }$$ の内部に含まれる全電荷が $${ Q }$$ であるとき、閉曲面 $${ \mathcal{S} }$$ を貫く電気力線の正味の本数は $${ Q / \epsilon_0 }$$ に等しい($${ \epsilon_0 }$$ は真空の誘電率を表す)
ここで、全電荷とは、閉曲面 $${ \mathcal{S} }$$ 内にある正電荷 $${ +Q_1 }$$ と負電荷 $${ -Q_2 }$$ を合わせて $${ Q = +Q_1 - Q_2 }$$ としたものをいいます。また、電気力線の正味の本数とは、閉曲面 $${ \mathcal{S} }$$ を内側から外側に向かって貫く電気力線の本数が $${ \Phi_1 }$$ で、外側から内側に向かって貫く本数が $${ \Phi_2 }$$ であるときに $${ \Phi = \Phi_1 - \Phi_2 }$$ のことをいいます。これらによって、ガウスの法則は $${ \Phi = Q / \epsilon_0 }$$ と表すことができます。

次に、ガウスの定理はこの記事でも書いた通り、以下の通りです:
3次元空間内のある領域 $${ \mathcal{V} }$$ とそれを囲む閉曲面 $${ \mathcal{S} }$$ を考えて、その面 $${ \mathcal{S} }$$ 上の微小面積要素 $${ \mathrm{d} S }$$ での単位法線ベクトルを $${ \bm{n} }$$ とすると、ベクトル場 $${ \bm{A} (\bm{x}) }$$ について
$$
\iiint_{\mathcal{V}} \left( \nabla \cdot \bm{A} \right) \mathrm{d} V
= \oiint_{\mathcal{S}} \bm{A} \cdot \bm{n} \mathrm{d} S \qquad (\bigstar)
$$
が成り立つ。左辺の $${ \mathrm{d} V = \mathrm{d} x \, \mathrm{d} y \, \mathrm{d} z }$$ は 3次元体積要素を表す。
このガウスの定理において、ベクトル場 $${ \bm{A} }$$ として電場 $${ \bm{E} }$$ を考えることでガウスの法則が導かれますが、その前に電場と電気力線がどういう関係であるか、というところから解説します。
電場と電気力線の関係
電気力線とは、空間内の各点の電場ベクトル $${ \bm{E} (\bm{x}) }$$ を滑らかに線でつなげたもの、ということができます。電気力線上の各点で、電場ベクトル $${ \bm{E} (\bm{x}) }$$ が電気力線の接線の方向を向くようにつないでいく、ということです。また、電場が強いところでは単位面積当たりの電気力線の本数が多くなるように、電場が弱いところでは少なくなるように書きます。具体的には、電気力線がある面を垂直に貫いていて、その面上での電場の強さが $${ | \bm{E} | }$$ であるとき、電気力線はその面の $${ 1~\mathrm{m}^2 }$$ 当たりを $${ | \bm{E} | }$$ 本が貫いている、と約束します。
電気力線が面を、垂直ではなく斜めに貫いているときには、どう考えればよいでしょうか? この場合は、下図右で示されている角度を $${ \theta }$$ とすると、面 $${ 1~\mathrm{m}^2 }$$ 当たりを貫く電気力線の本数は $${ | \bm{E} | \cos \theta }$$ となります。面の単位法線ベクトル $${ \bm{n} }$$ を使って表すと、$${ \bm{E} \cdot \bm{n} }$$ とすることもできます。つまり、電場 $${ \bm{E} }$$ の法線方向成分に等しくなるわけです。

なお、面には「向き」が定義されていて、その「向き」にしたがって単位法線ベクトルの向きが決められているとします。そして、上図のような場合は $${ \bm{E} \cdot \bm{n} > 0 }$$ ですが、電気力線が上図とは逆の向きに面を貫いている場合は $${ \bm{E} \cdot \bm{n} < 0 }$$ となることに注意します。
面上の面積要素を $${ \mathrm{d} S }$$ とすると、この面積要素を貫く電気力線の本数は $${ \bm{E} \cdot \bm{n} \mathrm{d} S }$$ と表されるので、閉曲面 $${ \mathcal{S} }$$ 全体での本数は、これを積分して
$$
\oiint_{\mathcal{S}} \bm{E} \cdot \bm{n} \mathrm{d} S
$$
となります。閉曲面の場合、単位法線ベクトル $${ \bm{n} }$$ は閉曲面が囲む領域から外に出ていく向きを持ちますので、電気力線が閉曲面 $${ \mathcal{S} }$$ から出ていく場合は $${ \bm{E} \cdot \bm{n} > 0 }$$ で、閉曲面 $${ \mathcal{S} }$$ に向かって入っていく場合は $${ \bm{E} \cdot \bm{n} < 0 }$$ でカウントされます。このようにして、上の積分は初めの方で述べた、電気力線の正味の本数 $${ \Phi }$$ を表すことになります。

ガウスの法則とマクスウェル方程式
ここで、ガウスの定理の式 $${ (\bigstar) }$$ で、ベクトル場 $${ \bm{A} }$$ を電場 $${ \bm{E} }$$ とすると
$$
\iiint_{\mathcal{V}} \left( \nabla \cdot \bm{E} \right) \mathrm{d} V
= \oiint_{\mathcal{S}} \bm{E} \cdot \bm{n} \mathrm{d} S \qquad (\#)
$$
となり、前節で述べた通り、この式の右辺は閉曲面 $${ \mathcal{S} }$$ を貫く電気力線の正味の本数 $${ \Phi }$$ を表します。一方、左辺の $${ \nabla \cdot \bm{E} }$$ は「電場の湧き出し・吸い込み」を表し、それはマクスウェル方程式の中の一つである
$$
\nabla \cdot \bm{E} = \frac{\rho}{\epsilon_0}
$$
($${ \rho }$$ は電荷密度を表す)という式により書き直すことができます。この式は「電場の湧き出し・吸い込みは、正電荷・負電荷により発生する」ということを表す式です。この式の両辺を領域 $${ \mathcal{V} }$$ で積分することにより
$$
\iiint_{\mathcal{V}} \left( \nabla \cdot \bm{E} \right) \mathrm{d} V
= \frac{1}{\epsilon_0} \iiint_{\mathcal{V}} \rho \, \mathrm{d} V
$$
となり、電荷密度 $${ \rho }$$ の領域 $${ \mathcal{V} }$$ での体積積分は、領域 $${ \mathcal{V} }$$ に含まれる全電荷 $${ Q }$$ となるので、以上によりガウスの法則 $${ \Phi = Q / \epsilon_0 }$$ を導くことができました。
上記では、「マクスウェル方程式の一つを使ってガウスの法則を導く」ということをしましたが、逆に「ガウスの法則を前提としてマクスウェル方程式の一つを導く」ということもできて、そのような構成にしている本もあります。(例えば、有名どころで砂川重信著「理論電磁気学」紀伊國屋書店)
それは、閉曲面 $${ \mathcal{S} }$$ を貫く電気力線の正味の本数を表す式
$$
\Phi = \oiint_{\mathcal{S}} \bm{E} \cdot \bm{n} \mathrm{d} S
$$
をガウスの定理により書き直して
$$
\Phi = \oiint_{\mathcal{S}} \bm{E} \cdot \bm{n} \mathrm{d} S
= \iiint_{\mathcal{V}} \left( \nabla \cdot \bm{E} \right) \mathrm{d} V
$$
とし、一方でガウスの法則から
$$
\Phi = \frac{Q}{\epsilon_0}
= \frac{1}{\epsilon_0} \iiint_{\mathcal{V}} \rho \, \mathrm{d} V
$$
となって、この二式が任意の領域 $${ \mathcal{V} }$$ で等しくなければならないので、被積分関数どうしが等しい、つまり $${ \nabla \cdot \bm{E} = \rho / \epsilon_0 }$$ が成り立つ、というようにして示すことができます。
このように、マクスウェル方程式の一つである $${ \nabla \cdot \bm{E} = \rho / \epsilon_0 }$$ からガウスの法則 $${ \Phi = Q / \epsilon_0 }$$ を導くことも、その逆もできるわけですが、この二つは表現の仕方こそ違うものの同じものであると見なすことができます。なぜなら、「電場の湧き出し・吸い込み」を表す $${ \nabla \cdot \bm{E} }$$ は空間の各点で定義されている局所的な量ですが、これは「ある有限な閉領域を出入りする電気力線の正味の本数 $${ \Phi }$$ の、その領域を無限に小さくする極限をとったもの」と考えることができるからです。逆に、上でやったように $${ \nabla \cdot \bm{E} }$$ を有限な領域で積分すれば、$${ \Phi }$$ となります。つまり $${ \Phi }$$ という量は、有限の広がりを持った閉領域での「電場の湧き出し・吸い込み」となっているわけです。
こういうわけで、微分を使って局所的に表した式が $${ \nabla \cdot \bm{E} = \rho / \epsilon_0 }$$ で、これを有限の領域で積分した式が $${ \Phi = Q / \epsilon_0 }$$ ということであり、物理法則としては同じことを表していると言えます。
そして、このいずれの式も、純粋に数学的な考察だけでは決して導くことができない式です。なぜなら、これらの式は電場(あるいは電気力線の本数)と電荷(あるいは電荷密度)という本来は無関係の物理量の関係を与えているからです。元々は無関係である物理量の間に、実験的事実を基にして関係を与えるのが物理法則なのです。それに対して、ガウスの定理を表す式 $${ (\bigstar) }$$ や $${ (\#) }$$ は純粋に数学的な考察だけで導くことができる式です。このようにして、「ガウスの法則」と「ガウスの定理」は明瞭に区別できるといえます。
ガウスの法則を使った電場の求め方
このガウスの法則は高校物理の電磁気分野で学ぶわけですが、どのような目的のために出てくるのでしょうか? それは、「簡単な場合に電場を求められるようにしたい。ただし(高校の物理なので)なるべく微積分を使わずに」という事情であると考えられます。もちろん、「微積分を使わずに物理を理解する」というのは本来無理があります。しかし、高校生が数学で微積分を学ぶのは通常二年生の中頃(もしくはそれ以降)となるので、実際に高校生に教える立場からすると、「習いたてでまだ十分に習熟したとはいえない内容を、他の科目で使うのは気が引ける」というのも分かります。特に電磁気の場合、ちゃんとやろうとするとベクトル解析、つまり多変数の微積分が必要となり、これは大学レベルの数学です。例えば、ある 3次元空間内の領域 $${ \mathcal{D} }$$ に電荷が密度 $${ \rho (\bm{x}) }$$ で分布しているときに、静電場 $${ \bm{E} (\bm{x}) }$$ を求めるためには
$$
\bm{E} (\bm{x}) = \frac{1}{4 \pi \epsilon_0} \iiint_{\mathcal{D}}
\frac{\rho (\bm{x}')}{| \bm{x} - \bm{x}' |^3} \left( \bm{x} - \bm{x}' \right)
\, \mathrm{d} x' \mathrm{d} y' \mathrm{d} z'
$$
という、一般には三重積分を計算しなければなりません。でも、だからといって高校の物理から電磁気分野を除くというわけにもいかず、そこで積分して出てくる結果だけとりあえず与えて計算してもらおう、という苦肉の策がガウスの法則である、と言えます。ただ、苦肉の策とはいえ、対称性がよい場合には上記の三重積分を計算せずとも簡単に電場の強さを求められるので、便利であることは確かです。
高校の物理でのガウスの法則は、以下に述べるようにして導入されることが多いです:
クーロンの法則より、点電荷 $${ q }$$ が点電荷から距離 $${ r }$$ の地点につくる電場の強さ $${ | \bm{E} | }$$ は $${ | \bm{E} | = \dfrac{1}{4 \pi \epsilon_0} \dfrac{|q|}{r^2} }$$ で与えられる。この点電荷を中心とする半径 $${ r }$$ の球面を考えると、その球面の $${ 1~\mathrm{m}^2 }$$ 当たりを $${ | \bm{E} | }$$ 本の電気力線が貫いているので、球面全体での電気力線の本数は
$${ | \bm{E} | \times 4 \pi r^2 = \dfrac{1}{4 \pi \epsilon_0} \dfrac{|q|}{r^2} \times 4 \pi r^2 = \dfrac{|q|}{\epsilon_0} }$$
となる。よって、球面全体での電気力線の本数は、球の内部に含まれる電荷のみで決まり、球の半径に依らない。このことは球面に限らず任意の閉曲面で成り立つことが知られている。つまり点電荷をどんな閉曲面により囲ったとしても、その閉曲面を貫く電気力線の本数は囲い方によらず一定となる。また、電荷の形状について、点電荷に限らず電荷が広がりをもって分布している場合でも成り立つ。
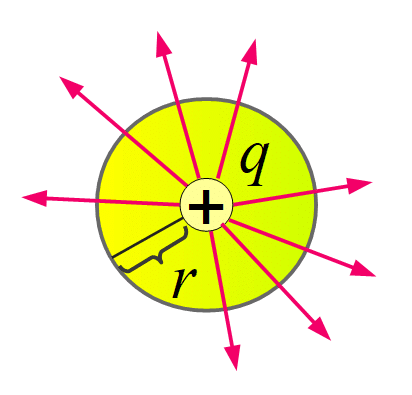
このように、クーロンの法則を前提として点電荷がつくる電場の式を与え、ガウスの法則が成り立つ簡単な例を一つ挙げて済ませることが多いです。クーロンの法則を前提とするのは、おそらく力学で万有引力の法則を先に学んでいるので、その類似性から考えやすいであろう、という意図なのでしょう。しかし、理論の構成の仕方としては、ガウスの法則の方が基本法則で、クーロンの法則はそれから導かれる、という方が自然です。
つまり、点電荷 $${ q }$$ がその周囲につくる電場の強さを求めるために、点電荷を中心とする半径 $${ r }$$ の球を考え、その球面を貫く電気力線の本数がガウスの法則から球面全体で $${ q / \epsilon_0 }$$ 本であると分かるので、球面の $${ 1~\mathrm{m}^2 }$$ 当たりの本数は $${ \dfrac{q}{\epsilon_0 \cdot 4 \pi r^2} }$$ で、この絶対値が求める電場の強さに等しい、と言えるわけです。
このように、点電荷が周囲につくる電場の強さは、クーロンの法則というよりはガウスの法則から求められるわけですが、このほかに「球全体に一様に電荷が分布している場合」や「無限に広がった平板に一様に電荷が分布している場合」にも、ガウスの法則から電場の強さを求めることができます。
では、ガウスの法則を用いて簡単に電場の強さを求められるのは、どのような場合でしょうか? 上で「対称性がよい場合」と書きましたが、もう少し具体的に書きます。ポイントは二つあります:
各点での電場の向きが、対称性などから分かること
各点での電場の向きに垂直となるような閉曲面をとったとき、その表面積を容易に求められること
まず 1. について、例えば点電荷や球全体に一様に帯電しているような場合、特別な角度方向はなく、どの方向も同等でなければならないので、電場は中心から放射状に広がっていると考えられます。また、無限に広がった平板に一様に帯電している場合は、その平板を挟んで両側が対称、かつ片側の各点で同等でなければならないので、電場は平板に垂直になっていると考えられます。このように対称性などから電場の向きが分かることが必要です。
次に 2. について、前々節で述べたように面 $${ 1~\mathrm{m}^2 }$$ 当たりの電気力線の本数は、面の単位法線ベクトルを $${ \bm{n} }$$ として $${ \bm{E} \cdot \bm{n} }$$ で与えられるので、電荷を囲む閉曲面を選ぶ際に $${ \bm{E} }$$ と $${ \bm{n} }$$ が同じ方向となるようにしておけば、面 $${ 1~\mathrm{m}^2 }$$ 当たりの電気力線の本数がそのまま電場の強さに等しくなって便利です。また、ガウスの法則で求められるのは閉曲面全体での電気力線の本数なので、電場の強さを求めるには、その本数を閉曲面の表面積で割らなければなりません。このような事情で、2. が条件として必要です。
「球全体に一様に電荷が分布している場合」や「無限に広がった平板に一様に電荷が分布している場合」は、ガウスの法則を使って電場の強さを求める問題として教科書や問題集によく出てきますが、その解説を読んでも意味がよく理解できないことがあるかもしれません。そのようなときに、上で述べたことが理解のヒントになれば幸いです。
以上、「ガウスの法則」と「ガウスの定理」の違いと関係性、ガウスの法則の意味や使い方について述べてきました。電磁気を学んでいる過程で、ガウスの法則あたりがよく分からない、というときに参考にしていただければ幸いです。
この記事が参加している募集
この記事が気に入ったらサポートをしてみませんか?
