
コンピューターサイエンス概論#6(7週目)
年初から色々立て込んでおり、毎週更新予定が月1に…。
おかげさまで残暑の頃にはうれしいご報告ができるかもです(筆者の状況なんてどうでもいいかもですが)。
流行り病もなんだかアホみたいな議論してますね。リスクの評価をインフル並みにするならインフルと同程度の対策すればいいわけで、リスク評価を下げてるのにまだ感染するかもしれないから油断できない!とかさ…。感染しても大半の人には大したことないですよ、という話なので、「感染しないことに全力」でなく、「感染したら休もう」程度になる話ですよね。マスクしながらエスカレータ駆け下りてるのとかね。安全より安心のトホホな現状。
さて、前回は関数を掘り下げる内容でした。
特に値渡しと参照渡しは大事な概念なので理解しましょう。ポインタの理解の入口にもなります。裏側の仕組みがわかるとスッと腑に落ちるものです。
リーディング課題
この週以降リーディングの課題はありません。基礎部分でしっかり読んで土台を作って徐々に深彫りする感じですね。
関数の使い方
今回は関数の使われ方をメモリの観点も含めて見ていきます。メモリの観点から派生して配列も見ます。
まず、関数というのは繰り返し実行される処理を再利用可能にするという側面があります。例えば、nのm乗を毎回ループしてたらコードが汚くなるので関数にnとmを渡して結果を受け取ったり、ですね。
基本的に関数というのは問題を小さくして小さい単位で解くパーツになります。この考え方はアルゴリズムでの基本になります。小さい問題の方が簡単なわけです。
問題を分割して繰返し処理する代表的な手法として
Iterative(ループによる反復)
Recursive(再帰呼び出し)
の2種類があります。
ここでは階乗(1からnまで掛け合わせたもの)を例に説明します。再帰関数の説明の有名どころは階乗とフィボナッチ数列ですね。フィボナッチは複数の再帰呼び出しがあって、少し説明が複雑になるのでアルゴリズムの回を作ったら説明します。計算量の説明とかでもフィボナッチは有用ですが、ここではまだ早いかな、と。
Iterativeな階乗
階乗の定義は
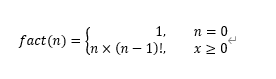
となります。0!は1と定義されているのに注意が必要です。
Iterativeに書くと
#include <cassert>
long iterative_fact(int n) {
assert(0 <= n);
int res = 1;
if (n > 0) {
for (res = n; n > 1; --n) {
res *= (n - 1);
}
}
return res;
}こんな感じですかね。定義に従っていますが、自分が書くならループは2からnまで回しますかね。減算は結構ミスが起きやすかったりします。C++だとsize_t型使ってたりするとハマりがちですね。
ちなみにループをよく見てもらうと最初の定義で戻り値用の関数をnで上書きしてからn-1を掛けていって、n-1が1になったところで終了します。0 > nとすると全部ゼロになるので注意です。こういうミスしがちな部分は境界線のテストで確認しましょう。
一応負の場合assertしてますが、まぁ、この辺は契約ではじいても良いかと。
Recursiveな階乗
これを再帰で実装してみます。
再帰関数を実装する場合、再帰呼び出しを止めるbase caseの引数を定義します。これは最も単純な問題で処理が始まるようなイメージで、その開始地点になる値です。例えばマージソートは配列を半分に分けながら再帰を行いますが、1つの要素しかない配列になったところがbase caseです。比較対象がないので、比較なしにそのまま結果を返せます
マージソートは再帰を使った分割統治法(divide and conquer)の例で使われます。これもアルゴリズムの記事を書いたら説明します。
階乗の場合のbase caseは0ですかね。0まで再帰すると最後が1を掛けるのが2回続いてしまうのですが。
1 #include <cassert>
2
3 long recursive_fact(int n) {
4 assert(0 <= n);
5 if (n == 0) {
6 return 1;
7 }
8 return n * recursive_fact(n - 1);
9 }これは処理が頭でイメージしにくいです。ちなみに僕はコンピューターサイエンスの勉強をする前に再帰関数を書いたことなかった気がします。再帰の方がコードはシンプルになります。
では、処理を見ていきましょう。
まず、 recursive_fact(4)を呼んだとします。
下記のように実行されます。
recursive_fact(4)
(8): return 4 * recursive_fact(3)
recursive_fact(3)
(8) return 3 * recursive_fact(2)
recursive_fact(2)
(8): return 2 * recursive_fact(1)
recursive_fact(1)
(8): return 1 * recursive_fact(0)
recursive_fact(0)
(6): return 1
(8): return 1 * 1
return 2 * (1 * 1)
return 3 * (2 * (1 * 1))
return 4 * (3 * (2 * (1 * 1)))
実際にはカッコ内は計算されてからreturnされますが簡単のため。
関数が展開されて、base caseの結果が返されると呼び出し元が順に計算されて結果が返ります。実際と違いますが、もう少しわかりやすく書くと
recursive_fact(4)
4 * recursive_fact(3)
4 * (3 * recursive_fact(2))
4 * (3 * (2 * recursive_fact(1)))
4 * (3 * (2 * (1 * recursive_fact(0))))
4 * (3 * (2 * (1 * 1)))
4 * (3 * (2 * 1))
4 * (3 * 2)
4 * 6
24
差異
Pros
読みやすさ
Cons
計算効率
メモリの使い方
再帰でのメモリの使われ方
ここでメモリの話になります。StackOverflowというエラーを見たことがあるでしょうか?Javaだとたまに出ますね。StackOverflowExceptionというやつです。プログラムを実行するとメモリ上にプロセスの領域が確保されます。下記のような構成になっていて、説明をわかりやすくするために天地逆転しています。
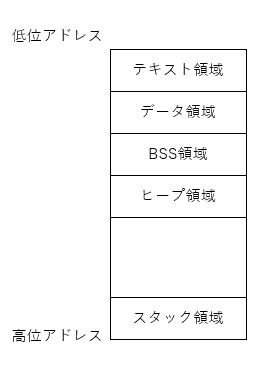
テキスト領域には実行されるプログラムが、データ・BSSは静的データですね。ヒープにはユーザーで確保する関数等スコープをまたいで利用する動的なデータが保持されます。C系だとmallocや色んな言語のnewとかはここに作られたりします。言語によっては解放してあげないとメモリリークに繋がる領域です。この辺はOSの記事を書いたら詳しく説明します。
それで、今回大事なのはスタック領域です。スタック領域は基本的には関数内で使われる変数とか一時的な値を保持するのに使われます。また、大事なのは関数呼び出しの際に、呼び出し元の情報を保持するためにも使われます。呼び出した関数の実行が終わった後にどこまでまでスタックを戻せばいいかの情報があって、関数の戻り値と一緒に呼び出し元の世界を再構築するイメージです。
ちなみにスタックに関してはデータ構造の基本中の基本なので、初心者でも知らない人はスタックとキューくらいは完璧に理解しましょう。スタックは皿を積むように上に乗せていって、取り出すときは上からしか取れない、と言った説明がよくされます。要は後入れ先出しです。ポテチの筒みたいなものです。関数でA地点からデータを積んでいって、終了したらA地点まで解放するようなイメージです。
プロセスの図を見るとヒープとスタックの間に空間がありますが、ここが実行時に使える空き領域です。ヒープは低位から、スタックは高位から空き領域の中間に向かって伸びていって、領域が枯渇するとStackOverflowのようなエラーが発生します。
再帰では呼び出しの度に関数に戻るための情報を積んでいるのでスタックがどんどん埋まっていくため、呼び出しが多すぎるとプログラムが強制終了されてしまいます。言語によって再帰の呼び出し数を制限してたりして、pythonでは最大再帰数を下記のように取得できます。
import sys
print(sys.getrecursionlimit())デフォルトは1000みたいで変更できるようです。
再帰的階乗のメモリの使われ方
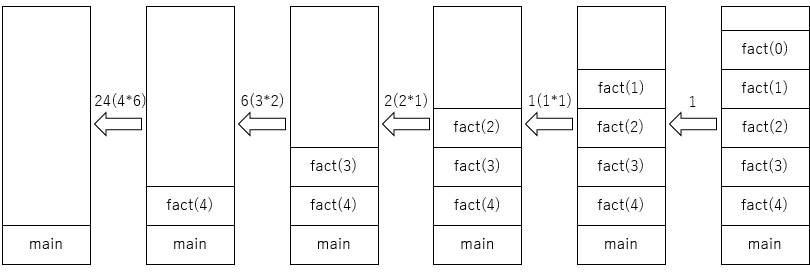
main関数から始まり下記のようにメモリの領域が関数呼び出しごとに確保されていきます。ちなみにこの四角はスタック領域と思ってください。実際は上限は可変です。また、スペースの関係上関数名はfactとさせて頂いています。

base caseにたどり着くと結果を返しながら関数で使っていたスタック領域が解放されていきます。
スタックとヒープの違い
簡単に説明しましたが、プロセスのメモリ領域内でのヒープとスタックの使われ方の違いです。大学1年の入門コースでもちゃんとメモリの説明してますね。初心者はメモリの使われ方、中級者ではキャッシュの使われ方、それ以降だと並列実行時のリソースの使われ方の理解が期待されると思います。この辺はしっかり押さえましょう。これがわかってると、例えばC++でローカル変数をクラスのポインタに設定するとどうなるか、とか理解できると思います(C++のコンストラクタでポインタ変数にデータを設定する時に一時的にローカル変数で計算したりすると面白いことが起きる)。
静的データと動的データ
静的データ
コンパイル時に領域が不定のアドレスに決まるデータ
グローバル変数とかstatic変数
ヒープに保持
動的データ
実行時に領域が一時的に確保されるデータ
無名だけど保持する必要のあるデータ(代入前に計算に使われるとか)
明示的にメモリ確保する場合ヒープに保持
明示的にメモリ確保しない場合スタックに保持
メモリリーク
メモリリークはメモリ確保がプログラムでできる言語において(もしくは自動でする言語の不具合で)確保したメモリが解放されない場合に、そのアドレスから始まる型に必要なサイズ分のメモリが使用されないのに確保されたままになる現象です。基本的にヒープ領域で発生します。
ヒープのメモリはスコープを跨いで生存するため、明示的に解放が必要な言語では注意が必要です。C++ではスマートポインタであったり、デストラクタで解放する構造を使うテクニックがあったりします(名前忘れた)。
配列
メモリに関連したデータ構造として、最も使用される配列(Array)です。
まずは普通の配列を取り上げます。C++でいうと int arr[10]のようなやつです。普段モダンな言語を使っていると動的配列という拡張したものを使っていると思います。そちらも後ほど取り上げます。
配列は連続したメモリ領域にデータが配置されるため、キャッシュ効率が良いです。ランダムアクセスも可能です。基本的にはデータの開始位置と型とサイズがわかれば、
n番目のデータのアドレス=配列のデータ開始アドレス + (型のサイズ×n)
でデータが取得できるということです。ここではnは0-originです。データの開始位置に最初のデータがあるのでindex(添え字)=0は開始位置になりますね。リストは連続していないので順次アクセスしかできません(データと次のアドレスの情報を持っている)。
デメリットとしては連続したメモリの領域に配置されるということはサイズ分の領域を確保しなければならず、10個の領域を確保して3個しか使わないと確保したメモリが無駄になります。また、10個の領域を確保していて11個目が使いたくても使えません(動的配列なら使えます)。いくつ要素があるかわからない場合使いにくいという特徴があります。競技プログラミングだと大抵上限のサイズで初期化します。単純で高速で動く静的配列と管理コストがあるけど制約の少ない(最大要素数はある)動的配列、という感じです。
配列のアクセスや代入はほとんどの言語で[]を使ってします。
1つ目の要素はarr[0]という感じです。ここでarrは配列を持った変数です。
簡単な配列を使ったコードを書くと…
#include <iostream>
int main() {
int arr[10];
arr[0] = arr[1] = 1;
for (int i = 2; i < 10; ++i) {
arr[i] = arr[i-2] + arr[i-1];
}
for (int i = 0; i < 10; ++i) {
std::cout << arr[i] << " ";
}
std::cout << std::endl;
return 0;
}何をしてるコードかはわかる人にはわかるかと。
動的配列でなく、C++では初期化時のサイズがわからない場合にポインタを使った動的"な"配列の定義もできます。下記のようにすると入力値で配列が作れます。
#include <iostream>
int main() {
int n;
std::cin >> n;
int* arr = new int[n];
for (int i = 0; i < n; ++i) {
arr[i] = i * i;
}
for (int i = 0; i < n; ++i) {
std::cout << arr[i] << " ";
}
std::cout << std::endl;
delete [] arr;
return 0;
}とは言え、サイズも渡さないと関数呼び出しできなかったり使い勝手はよくないです。
そこで標準ライブラリにあるvectorという動的配列がよく使われます。
この動的配列はデータ構造の記事を書いたら詳しく書きますが、容量が一定まで埋まったら、新しく2倍の容量を確保して、データをコピーします。つまりn個の連続した領域を確保していて、一定以上埋まると2n個の領域をコピーして要素をコピーしてアドレスが変わる、という流れになります。
課題
今回も課題はデザインパートと実装パートに分かれています。
今週はデザイン部分です。問題は2問あります。
問題文
単語頻度カウント
あなたは文か段落に指定された単語が何回出現するか数えるプログラムを作ることになりました。まず、ユーザーは文(または段落)を入力します。その後、カウント対象の単語を任意の個数入力します。対象の単語は1つずつ入力するのでなく一度に入力され、それがいくつかわかりません。この際、ヒープに保存される動的に領域を確保された配列を利用してください。静的配列の場合、点数は与えられません。また、メモリリークも起こしてはいけません。大文字と小文字の区別はせず、theとTheは同一単語と扱ってください。
また、入力の文または段落はCスタイルの文字列(配列で最後がnull文字'\0')を利用し、単語に関してはC++スタイル文字列(string)を使っても良いです。
[Extra Credit]
入力単語にもCスタイル文字列を使うと加点があります再帰によるフラクタル
アスタリスク(*)と空白を使って以下のようなパターンを作成するpattern関数を作って下さい。この関数は再帰呼び出しを行います。
再帰的な思考で2つの再帰呼び出しを含む7~8行でコードを書いてください。関数の定義は下記になります。
// 概要:
// パターンの最長の行はi列目から始まるn個の星として出力されます.
// 例えば下記の例はpattern(8, 0)で生成されます。
// 事前条件: nは0より大きい2の乗数
// 事後条件: 例のようなパターンが出力される
void pattern(int n, int i);出力例
*
* *
*
* * * *
*
* *
*
* * * * * * * *
*
* *
*
* * * *
*
* *
*
ヒント:
どうやってフラクタルを作れるでしょうか。全体のパターンの中に2つのパターンを見つけられるでしょうか?有用と思われるスニペットです。
// iこの空白を出力する:
for (k = 0; k < i; k++) cout << " ";
// n個のアスタリスクと空白を出力する:
for (k = 0; k < n; k++) cout << "* ";個人的には一行のループは修正時にバグを出しやすいので{}で囲むスタイルを好みます。
[Extra Credit]
ループによる繰返しで同じ処理をするプログラムを書く
デザイン
今週の課題はデザイン部分です。内容は前回同様です。
問題の分析
ユーザーの入力/要求およびプログラムの出力は何か
どんな想定をしているか
プログラムを分解した場合のタスクとサブタスクは何か
プログラムのデザイン
プログラムの概要
必要なデータとユーザーの入力タイミング
プログラムはどんな決定をする必要があるか
タスクは繰り返されるか
どうやってプログラムをモジュール化するか、関数はいくつ必要か、それは何か
どんな不正な入力が想定されるか
テストケース
正常値
異常値
境界線
この記事が気に入ったらサポートをしてみませんか?
