皆既日食に至るまでの被覆率は食分でどう変化する？（解説）

問題はこちら：

答え：以下の式

　皆既日食で食分Lに対する被覆率Rは上式となります。この式をどう導出するか解説します。

解説1：扇形から三角形の面積を引く

　今回の問題を図で確認してみましょう：

　月と太陽の見かけの直径を1としておきます。こうする食分Lが0～1の範囲になって便利です。月の中心をP、太陽の中心をQとし、交点をA、Bとします。被覆率は図の赤線で囲まれた面積を円の面積で割れば求まります。

　この赤線の領域は図の対称性からオレンジの領域の倍の面積になっているのは明らかですよね。よってオレンジの領域の面積を求めれば良い事になります。これは扇形PABから図の黄色い三角形を引けば求まります。扇形PABの面積は図の中心角θが分かれば算出できますし、黄色い三角形の面積はPCとACの長さが分かれば一発です。

中心角θから扇形の面積を求める

　黄色い三角形は直角三角形です。これはABが弦でPQを含む直線が円Pの中心を通っているので∠ACPが直角になる事から明らかです。ここから三角比が使えます。具体的には中心角θは辺APとPCの比から、

で直接求める事が出来ます。APの長さは半径1/2である点に注意です。

　PCの長さを求める道筋を見つけてみましょう：

　図の対称性から、点Cが線分DEの中点なのがわかりますよね。DC＝DP+PCなので、PC=DC-DPです。DPは円の半径なので1/2。つまり、

となります。DCはDEの半分で、DEは図にあるように、

なので、PCの長さは、

と食分Lの式で表現できます。という事で中心角θは、

となるのがわかりました。

　中心角θが分かれば扇形の面積S1は円の面積がπr²なので（r=1/2）、

と食分Lのみの式で表現できます。

三角形の面積を求める

　次は黄色い三角形の面積S2です。これは、

が自明ですよね。PCの長さは既に(1-L)/2とLで表現できていますから、ACの長さをLで表現すればS2が求まりそうです。

　ACは三平方の定理から、

ここからS2は、

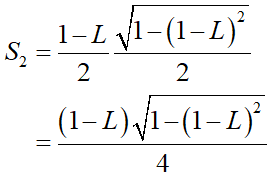
となります。

　これで必要な面積が揃いました。被覆されている部分の面積Sは、扇形の面積S1から三角形の面積S2を引いて（＝オレンジ領域の面積）それを2倍すれば良いので、

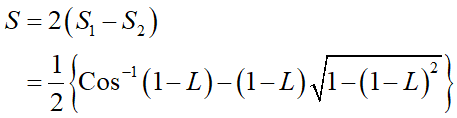
整理すると上式のようになります。

　欲しい被覆率Rは太陽の見かけの面積（πr²）に対する面積Sの割合なので、

以上の式となりました。蛇足ですがα=1-Lとすると、

少し整理された見た目になります。

解説2：積分で面積を求める

　被覆している面積を積分でダイレクトに求める事もできます。下図のように想定してみます：

解説1の冒頭に挙げたオレンジの半月領域は、上図のオレンジの領域の2倍、被覆範囲は4倍に相当します。図のtから右端までの幅が食分の半分に当たりますので、

です。展開が煩雑になるのでしばらくはtのままで進めます。

　オレンジ領域の面積Sを積分で求めます。

面倒くさいルートを無くしたいので、

と置きます。

dxは上式右辺に差し変わり、xの範囲も右のθの範囲になるので、

上式のように展開できます。積分内が大分簡単になりました。sin²θはcosの2倍角の公式を利用しべき乗を無くします：

これを上式に代入するとさらに簡単になりますね：

　右辺のsin(…)の所がちょっとごちゃついていますので、落ち着いて整理してみましょう。sinの中は2倍角になっているので次のように展開できます：

三角関数の中に対応する逆三角関数が入ると値が元に戻る性質をうまく使います。これで三角関数は消えてなくなり、シンプルなルートの式に化けてくれました。

　最後にtを戻してあげると、

これが解説２冒頭のオレンジ領域の面積です。この4倍が被覆面積で、太陽の面積はπr²なので、被覆率Rは、

無事に解説1と同じ式が導出できました。やれやれです(^-^;

深掘：被覆率と暗さの感覚

　被覆率Rが食分Lで求められるようになりました。LとRのグラフはこんな感じになります：

　月の見た目の位置は天球の局所的には等速（等角速度）で移動していくので、Lは時間にほぼ比例して増えていきます。つまり上のグラフは横軸を時間と捉えても差し支えないですよね。

　これを見ると、蝕が始まった直後は食分が進行してもあまり被覆率が増えませんが、時間が経つにつれて被覆率が加速していくのがわかりますね。実際Rの式を微分すると、

こういうすっきりした式になり、このグラフを描くと、

傾きが単調増加で増え続けていますので、被覆率の増分が加速しているのがわかります。

　被覆率が増える程太陽からの光の量は減ります。このため、皆既日食を観察していると被覆率が増える後半になると周囲が加速度的に暗くなるのを感じる事ができます。

　また人の感覚というのは一般的に物理量に対して比例していない事が知られています。例えば音量（音圧）は圧が半分になっても人の耳は殆ど音量が下がっていないように感じます。

　これはおそらく光量にもあり、光量が半分になったとしても、人の目（脳の感覚）は半分までは減っていないと認識するんじゃないかなと思われます（この辺り良い文献が見つからなかったため憶測です）。それを踏まえて、食分の進行度と人の目が感じる暗さの度合いをグラフ化してみましょう。

　今回の問題で求めた被覆率Rは数値が大きくなる程光量が減ります。つまり光量の割合Cはその逆、

と考えて良いでしょう。先のグラフを横軸を食分L、縦軸を光量Cにすると、

上に凸のグラフに変わります。さらに人の明るさの感覚をYとし、それが光量の割合Cに対して2乗根な関係（明るさの過大評価）にあると仮定すると、

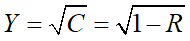
皆既日食の食分Lに対する明るさの感覚を表す一つのモデル式ができました。グラフにすると、

このように食分Lが大きくなると急激に暗さが増したように感じるというグラフになりました。

　2012.5.21に東京で体験した金環日食でも、食分が半分を過ぎても周囲は少しだけ暗くなった…かな？というくらいの印象でした。しかし被覆率が大きくなった頃に急に周りが暗くなり、最大食間際で夕方と夜の間くらいの暗さにまで一気になり、気温もぐんと下がったのを良く覚えています。その急変はまるで嵐でも来るかのようで、神秘と共に恐怖も少し感じました。上のモデルは僕が想定した適当なものではありますが、実際こういう曲線的な暗さの変化を感じたのは確かです。

　光量と人の明るさの感覚は実験で概算値を出せると思います。今回の例では2乗根としましたが、例えば、

と累乗にパラメータaを入れたより一般化したモデル式を想定して、光量感覚実験をしてパラメータaを推定する実験をすれば、より感覚に近い曲線を描けるはずです。

　という事で今回は皆既日食からの問題でした。ではまた(^-^)/