4桁の整数同士の割り算で√2っぽい値を作ろう(解説)
問題はこちら:
答え:例えば以下の分数

1.4142よりも√2に近い4桁同士の分数は実は沢山あります。実際総当たりで調べてみると664パターンありました。皆さんは見つける事ができたでしょうか?
探し方は色々あると思います。最初に分母分子を調整する力技な方法でやってみます。次に数式をうまく使った方法で見つけてみます。
解説1:分母と分子を微調整していこう
√2は、

です。これに対し問題にある基準となる分数は、
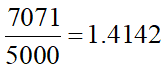
でした。√2よりもちょっと小さいですよね。よって少しだけ大きくできればより√2に近付く可能性があります。
分数は分子を大きくすると値が大きくなりますし、分母を大きくすると値が小さくなります。この性質を利用して微調整してみましょう。
今は値をちょっとだけ大きくしたいのですから、分子を7072にしてみます。すると、

おっと、これは逆に√2よりも大きくなってしまいました。値を小さくするために次は分母を5001にしてみましょう:

今度は√2よりも小さい方に振れたのでまた分母の値を一つ上げます:

また大きくなり過ぎましたが、こんな感じでじわじわと微調整を続けて行きます。すると程無くして、

この分数がすぐに見つかるはずです。√2との差は、

上が基準側で下が見つけたものです。より√2に近いですよね。微調整アルゴリズムで答えの一つを見つけられました!
解説2:連分数を使って見つけてみよう
√2は無理数なので有理数では表現できません。これは高校数学で習う基本事項です。しかし、実は連分数を使うと√2を整数の分数で表現する事ができます!
連分数というのは、分数の分母がa+b/cという形になっている分数です。例えば、

分母の分数の分母がa+b/cになっているのも連分数です:

整数で構成された連分数は一番下の分母から整理していくと単純な整数分数に直す事が出来ます:

√2をこういう連分数の形に書き直すとこの戻し作業で整数分数が導ける。その辺りがポイントになります。実際に展開してみましょう。
スタートは√2を整数部分と小数部分に分けます。つまり、

あえて右辺のように書けば第1項が整数部で、第2項が小数部になります。
次に小数部を分子が整数となる分数に変換します。第2項に√2+1を掛けると和と差の積なので√2が消えてくれますよね。すなわち、

こういう形にできます。分母の有理化の逆、いわば「分子の有理化」ですね。
上の分数、実はもう連分数の形になっています。そして右辺の分母に√2があるので、この連分数をそのまんま√2の所に埋め込む事ができます:

連分数が1段深くなりました。そしてまた最下段の分母に1+√2の塊が現れました。後は同じように展開していくと、連分数がどんどん深くなっていきます:

ここでもうお分かりかと思いますが、√2の連分数は無限に深くなります。この展開を無限に続ければそれは√2そのものではありますが、それだと戻し展開がいつまでもできません。
そこで適当な所で深化を終了します。そして最下段にある√2を0に置き換えます。すると整数連分数になります。もちろんそれはもはや√2ではありませんが、√2に近しくなっているはずです:

各深さで戻し展開してみると、

深くなる程精度が上がるのがわかります。そして戻し展開の結果は整数分数になっているのですから、ある深さの所で4桁同士の分数もでてくるはずです。
解説3:連分数を戻した時の分数は数列で表現できる!
さて、ではどれだけ深くすると4桁/4桁の分数になるのか?連分数は戻し展開が面倒くさいので、場当たり的にやるとちょっと骨が折れそうですよね。そこで次のように考えてみます。
途中で終了した時、連分数の一番下は常に次のような形になっていました:

この最下段の答えは3ですが、敢えてそれを3/1と表し、この分母をA1、分子をB1という数列の初項と捉えます:

次に一つ上の段まで戻し計算を進めます:

一つ上の戻し展開をした分母をA2、分子をB2とすると、

戻し2段目の計算結果が1段目の値から求まる事が分かります。戻し3段目も、

添え字が一つ繰り上がっただけで形は全く一緒です。この事からn段目の分母分子の値An、Bnは、

このようになり、連立漸化式の形になるのが分かります。
n段目が最後の戻し展開だとすると、

最終的な√2の近似分数は非常に単純な形になります。
上式は2つの漸化式が入っているので、さらにBnを消してしまいましょう。先の連立漸化式の上段の式からBn=An+1と表せますよね。それを代入すると、

数列Anだけの式で√2の近似分数が表現できてしまいました。後は数列Anがわかれば上式から具体的な√2の近似分数が導けます。
先の連立漸化式を解きます。今An=Bn-1と単純な関係があるので、それをBnの式に放り込んで数列Bnを消すと、

An+1が2つ前のAn-1およびAnから求まる事が分かります。いわゆる3項間漸化式の形になるんですね。今A1は1で、A2はB1と等しいので3でした。初項2つが定まっているので、数列Anが一意に定まります!
後は逐次的にAnの要素を求めていけば良いだけです。実際に求めてみましょう:

例えばA8=577の場合、

4桁同士の分数になり、結果も基準よりはるかに高精度なのがわかります!
さらに1段深いA9=1393の時はもっと精度が良くなるはずです:

上は小数点以下9桁目で四捨五入をいれていますが、小数点以下7桁目まで一致しています。A10=3363まで深くすると精度はさらに良くなりますが、分子の足し算が5桁になり今回の問題の条件から外れてしまいます。
このように数列Anを使う事で√2を近似する整数分数をいくらでも作っていける事が分かりました。非常に面白いですよね~。
解説4:終了時を「0」じゃなくて「1」にしても良い
解説3では連分数の深化を途中でやめて√2の所を0に置き換えて導きました。でもです、√2って少なくとも0より1の方がより近いですよね。真の値に近いという事は、同じ段数から戻し展開した結果は√2により近くなっているはずです。
解説3との違いは初期値だけです。A1とB1は、

よりA1=2、B1=5です。B1はA2と等しいのでA2=5。Anの3項間漸化式の関係は全く一緒なので、そこからAnの新しい数列が出来ます:

A9=2378の時、√2の近似値は、

小数点以下7桁目までは一致して、8桁目も真の方は「6」なのに対して上は「5」ですから近いですよね。解説3のA9=1393の時よりもさらに近しい値になりました。
実は4桁同士の割り算で求められる近似値としては上の8119/5741が一番精度が高いです。この分数を見つけられた方、お見事です!
深掘り:mが正の整数ならどんな√mでも分数数列を作れる
今回の√2の連分数近似ですが、これは別に√2だけではなく√3でも√5でも同じような展開が出来ます。一般化してみましょう。
mを正の整数とし、√mの整数部をaとします。mが平方数の場合、√m=aなので、あえて分数で書くなら、

です。
mが平方数でない場合、√mを整数部aと小数部√m-aに分けます:

括弧部分を和積の公式で分数化すると、

右辺が√mそのものなので、分母の√mをそれで置き換えると、

このように延々と続いていく連分数ができます。一番最下段の所で展開を打ち切り、√mの所をその整数部aに置き換え、少し整理すると:

整数連分数の出来上がりです。
次に最下段の分数の分母をA1、分子をBnとし、数列の初項とします:

戻し展開2段目は、

これより、

戻し展開3段目以降も同様の為、

上の漸化式が得られ、下段のBnとBn-1を消去すると、

を得ます。n段目で戻し展開が終わるとすると、

以上から、正の整数mとその整数部aがあれば以下の情報を用いて√mを近似する整数分数を求められます:
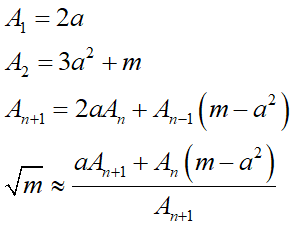
例えば√5なら、m=5とa=2なので、

こういう数列Anの要素が芋づる式に簡単に得られます。この数列を用いて例えばA5=1292、A6=5473を√mの式に代入すると、

小数点以下8桁まで一致している√5の近似整数分数をあれこれ探す事無く得られます!
終わりに
連分数は名だたる数学者がこぞって研究しています:
オイラー、ガウス、ラグランジュ、リーマンなどウルトラ有名数学者が名を連ねています。無理数√2が整数だけの分数で表現できるというのは、無理数と整数とを繋いでいるとも言えます。上のガウスの連分数ではなんとπも整数連分数で表現できてしまいます:
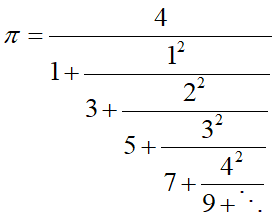
この規則正しい美しい表現…神秘としか言いようがありません。実際1,3,5…と奇数値になっている深さを17で計算してみたところ、

このような値に近似しました。小数点以下5桁まで一致しています。すげぇ…。連分数、神秘的で奥深い世界です。
ではまた(^-^)/
この記事が気に入ったらサポートをしてみませんか?
