
超基礎からの微分積分—増分6
関数
関数は、
座標上に線を書くことができます。

増分を関数に適応する
増分=増えた分なので、
増分を関数に適応すると、
増分=(関数の値が)増えた分
となります。

関数は、座標上で線を書き、
点を別のところへ運んでくれます。
すると、
点を別の場所に運ぶのに、
横xと縦yに行っていることが分かります。
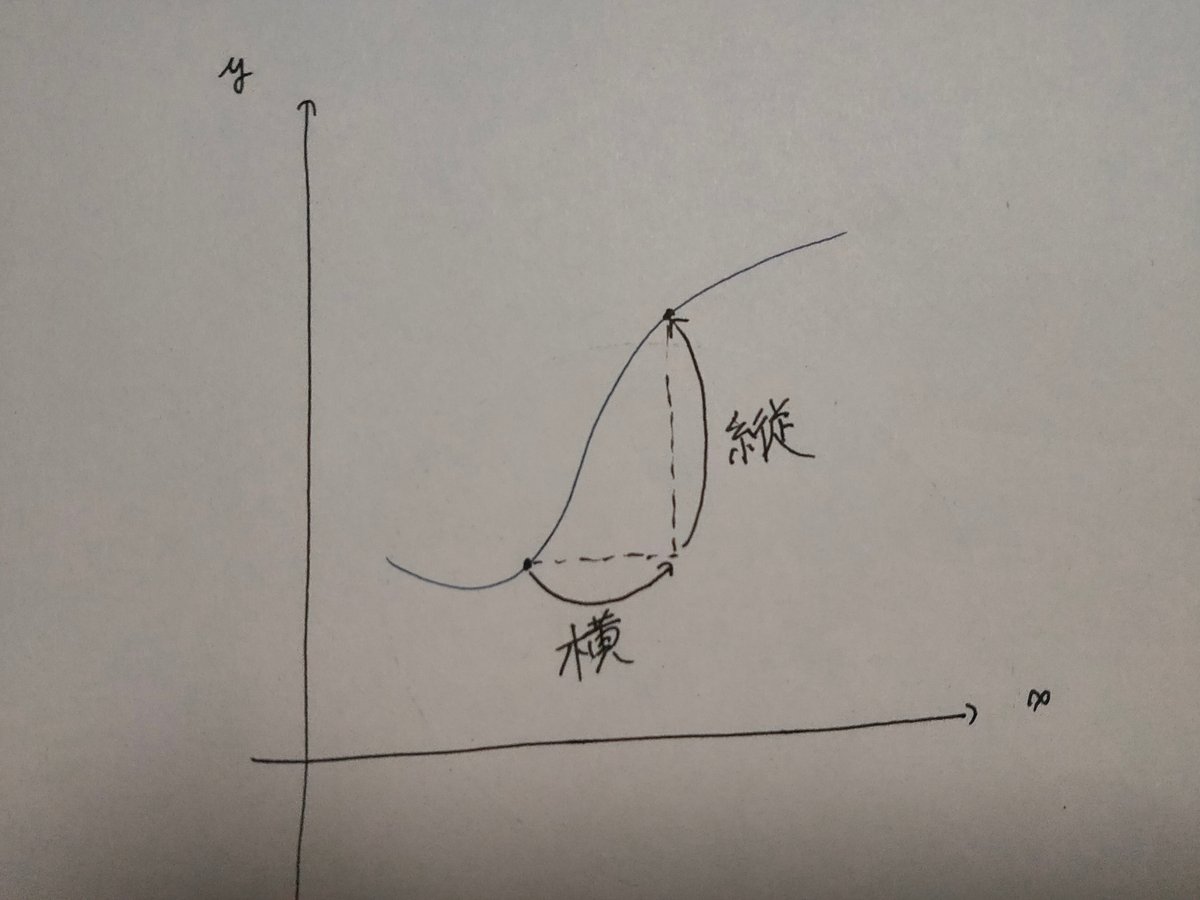
つまり、
ある点からある点までの
増えた分=増分を求めるためには、
横(x)と縦(y)の増えた分を求めなくてはならないようです。
練習問題
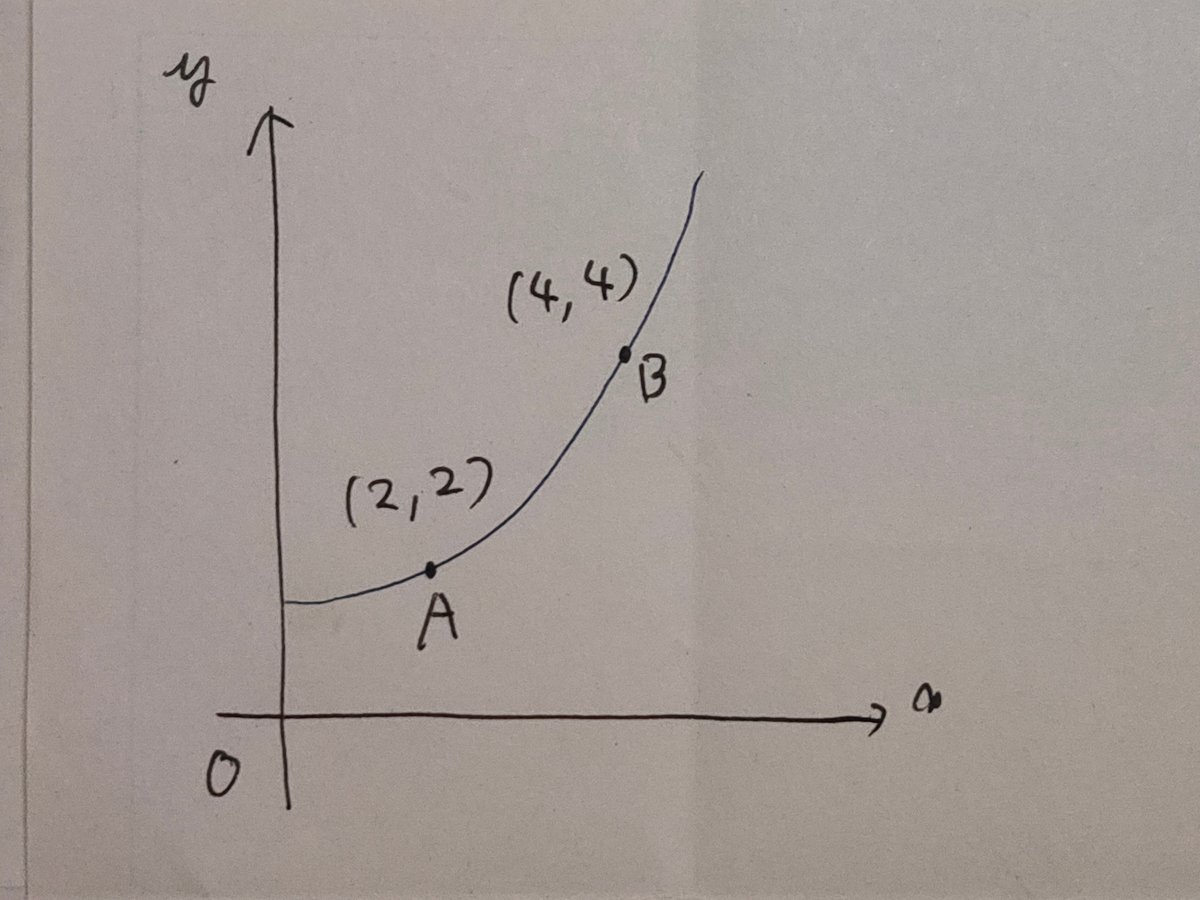
ある関数上の点Aから点Bまでの増分を求めてください。
(1)
解答
点Aは(x、y)=(2,2)、
点Bは(x、y)=(4,4)なので、
(2,2)→(4,4)となり。
x:2→4
y:2→4となる。
よって、
x:4-2=2
y:4ー2=2
したがって、増分は
xが2、yが2
(2)

解答
点Aは(x、y)=(4,4)、
点Bは(x、y)=(5,1)なので、
(4,4)→(5,1)となり、
x:4→5
y:4→1となる。
よって、
x:5-4=1
y:1ー4=ー3
したがって、増分は
xが1、yがー3
(3)

解答
点Aは(x、y)=(1,3)、
点Bは(x、y)=(5,3)なので、
(1,3)→(5,3)となる。
よって、
x:5-1=4
y:3ー3=0
したがって、増分は
xが4、yが0
(4)

解答
点Aは(x、y)=(1,1)、
点Bは(x、y)=(4,3)なので、
x:1→4
y:1→3となる。
よって、
x:4-1=3
y:3ー1=2
したがって、増分は
xが3、yが2
(5)

解答
点Aは(x、y)=(2,2)、
点Bは(x、y)=(4,4)なので、
xが2→4、
yが2→4となる。
よって、
x:4-2=2
y:4ー2=2
したがって、増分は
xが2、yが2
(6)

解答
点Aは(x、y)=(1,2)、
点Bは(x、y)=(2,1)なので、
xが1→2、
yが2→1となる。
よって、
x:2-1=1
y:1ー2=ー1
したがって、増分は
xが1、yがー1
(7)

解答
問題の図より、
xが0→2、
yが1→2となる。
よって、
x:2-0=2
y:2ー1=1
したがって、増分は
xが2、yが1
(8)

解答
問題の図より、
xが1→5、
yが3→5となる。
よって、
x:5-1=4
y:5ー3=2
したがって、増分は
xが4、yが2
#数学
#学問
#微分積分
#誰でも
#練習問題
#微積
#基礎から学ぶ
#数学入門
#1から学ぶ
#増分
#楽に学ぶ
最強の学びを発信するために頑張っています。サポートお願いします。
