
なぜ正規分布を標準正規分布に変換するのか
先生:「今日は正規分布と標準正規分布について勉強していこう。正規分布って知ってる?」
生徒:「なんとなく聞いたことはありますけど、正直よくわからないです。」
先生:「まず、正規分布は自然現象や社会現象でよく見られる形の分布なんだ。たとえば、テストの点数や身長のデータが正規分布に近いことが多いよ。特徴としては、平均が一番多くて、その値が山の頂点になる。そして、左右対称な形をしてるんだ。」
生徒:「平均が一番多くて、左右対称なんですね。それで、正規分布ってどういう式で表されるんですか?」
先生:「いいところに気づいたね。正規分布は次の式で表されるんだ。
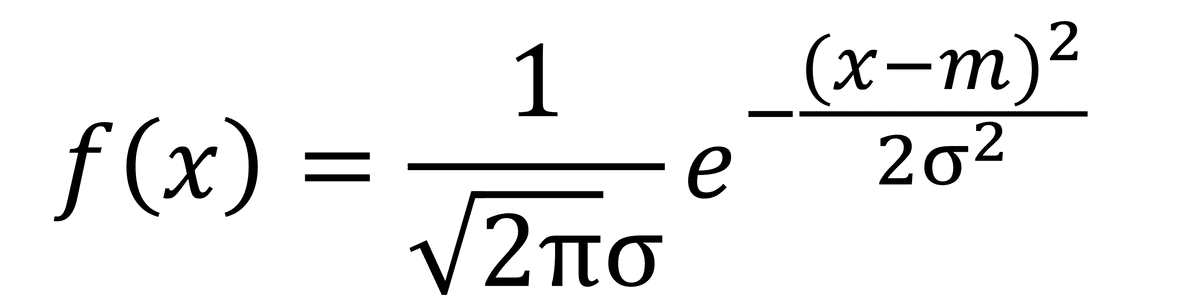
先生:「我々が知りたいのは、全体の中でどのくらいの割合か、つまり何%かを知ることなんだ。」
生徒:「なるほど、例えばテストの点数で自分がどのくらいの順位にいるかってことですか?」
先生:「そう、その通り!たとえば、テストで80点を取った生徒が全体の上位何%にいるか知りたいときも、正規分布を使う。これをもっとわかりやすくするために、具体的な例を考えよう。」
生徒:「お願いします!」
先生:「ある県の男性の平均身長が170cm、標準偏差が5cmだとする。このとき、身長180cm以上の人が全体の何%いるかを考えるんだ。グラフで考えると、180cm以上の面積に相当する。」
生徒:「じゃあ、その部分の面積を計算すれば割合がわかるんですね?」

先生:「そうなんだけど、積分して求めると計算がとても複雑になってしまう。普通の人にはちょっと無理かな。そこで便利なのが『標準化』だよ。」
生徒:「標準化って何ですか?」
先生:「正規分布は、平均 m と標準偏差 σ によって形が変わるんだけど、これを共通の形に変える方法が標準化なんだ。平均を0、標準偏差を1にして、どんな正規分布でも統一できるんだよ。式で表すと次のようになる。
こうして正規分布を標準正規分布に変換するんだ。」

生徒:「平均を0、標準偏差を1にするとどうなるんですか?」
先生:「そうすると、すべての正規分布が同じ形になるから、積分せずに表を使って簡単に割合を求めることができるんだ。これを使ってさっきの問題を解いてみよう。」
生徒:「ぜひお願いします!」

生徒:「なるほど!標準正規分布に変換することで表を使って計算が簡単になるんですね。」
先生:「その通り!まとめると、正規分布のままでは積分しないと割合が求められないけど、標準正規分布に変換すれば簡単に計算できるんだ。この変換を標準化と呼ぶ。これで理解できたかな?」
生徒:「はい!なんとなくぼんやりしていた部分がすっきりしました。ありがとうございました!」
この記事が気に入ったらサポートをしてみませんか?
